拉格朗日乘法与KKT条件

问题的引出

给定一个函数\(f\)，以及一堆约束函数\(g_1,g_2,...,g_m\)和\(h_1,h_2,...,h_l\).带约束的优化问题可以表示为

\[\min_{X \in R^n}f(X) \quad s.t. \; g_i(X) \leq 0 \; , \;h_j(X) = 0 \]

下面我们将来讨论具有上述问题的解，一共可以分为四种情况：

• 无约束条件
• 只有等式约束条件
• 只有不等式约束条件
• 同时有等式和不等式约束条件

无约束条件

我们先来复习一下多元函数取得极值的条件。设\(f: R^n \to R\),是一个连续可导的函数，并且\(J_f\)和\(H_f\)分别是\(f\)的一阶梯度和二阶梯度矩阵（Hession矩阵）,判断\(f(x^*)\)是它的一个极值的条件是：

• \(J_f=0,H_f\)是负定矩阵,则\(x^*\)是\(f\)的极大值
• \(J_f=0,H_f\)是正定矩阵,则\(x^*\)是\(f\)的极小值
• \(J_f=0,H_f\)是半正定或半负定或不定矩阵,则需要进一步讨论

这样，无约束下的最优化问题可以通过上述规则来求函数的极值。

等式约束条件

只含等式约束条件的最优化问题表示为（以一个等式约束为例）

\[\min_{X \in R^n} f(X) \quad s.t. \; h(X) = 0. \]

下面用具体的实例来讨论这一类问题，令

\[f(X)=x_1+x_2 \quad,\; h(X)=x_1^2+x_2^2-2 \]

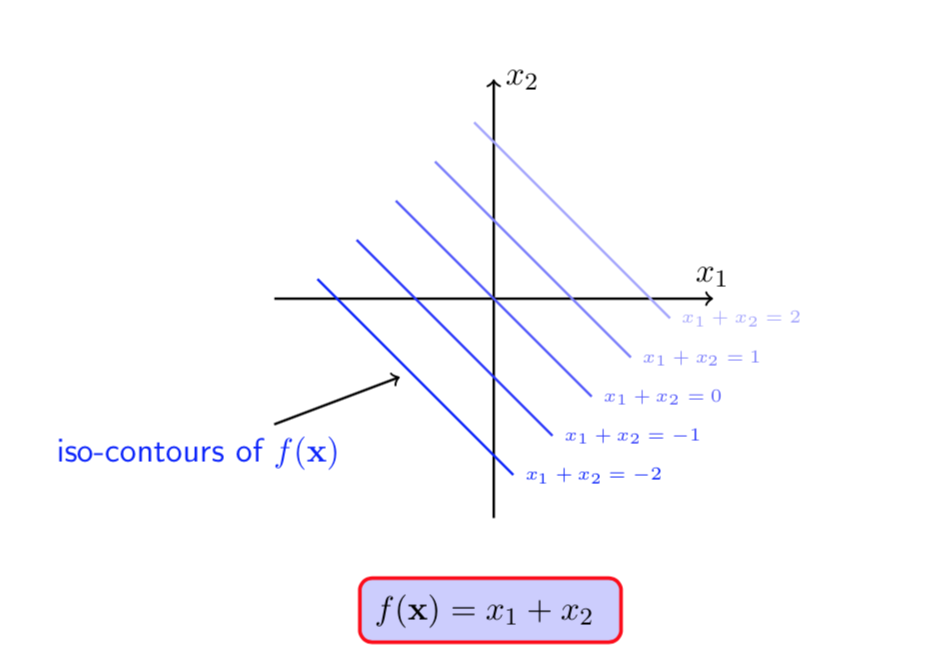
                              图（1 ）                                                        图（2）

在图（1）和（2）中蓝色线是\(f(X)\)的等高线，红色线是在\(h(X) = 0\)约束下的可行域（\(X\)可取值的可行范围）。

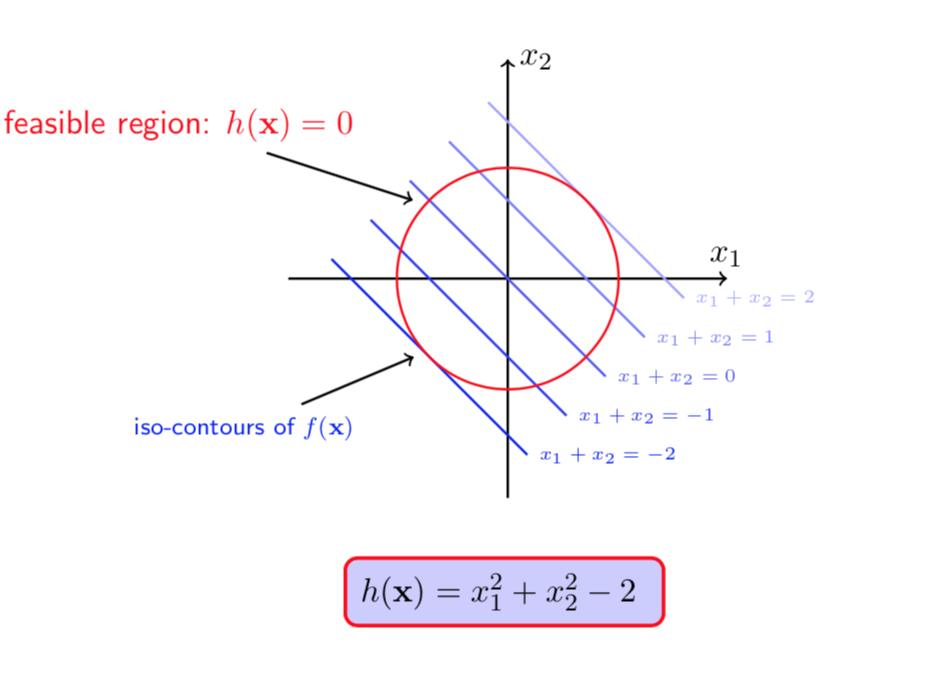
                              图（3 ）                                                        图（4）

为了找到\(f(X)\)的最小值。如图（3），我们需要从红色点的位置（点\(X_F\)）往某一个方向走一小步，并且目标位置依然在可行域内(满足\(h(X)=0\)的限制），同时还希望\(f(X)\)的值能够下降，即

\[h(X_F + \Delta X) = 0 \quad and \quad f(X_F) >f(X_F+ \Delta X) \]

我们知道沿着梯度的反方向是下降最快的。如果要满足\(\quad f(X_F) >f(X_F+ \Delta X)\)则必须有

\[\Delta X \cdot (-\nabla_x f(X)) > 0 \]

意思就是说，下一步走的方向\(\Delta X\)应该与\(-\nabla_Xf(X)\)的夹角小于等于90度。

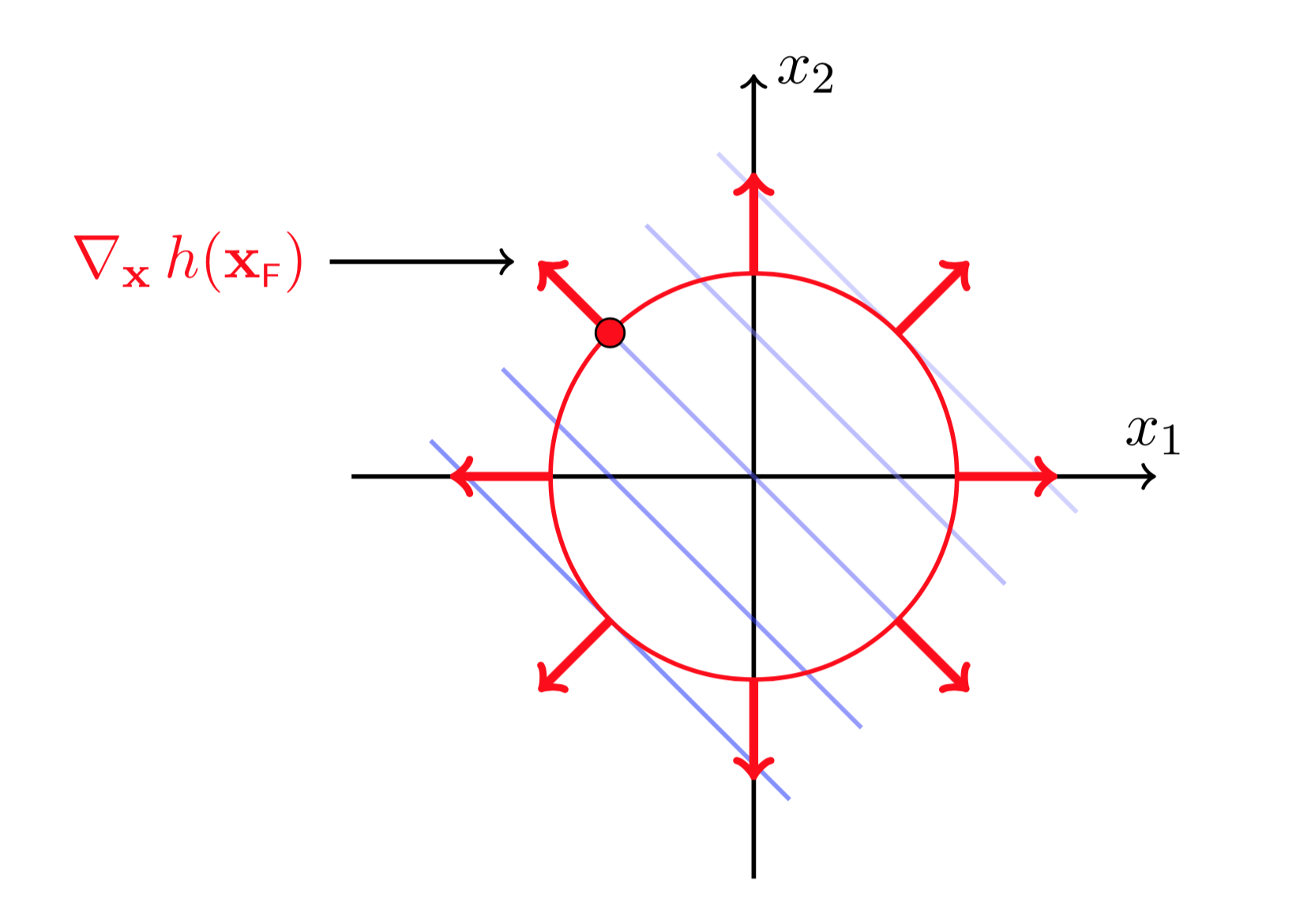
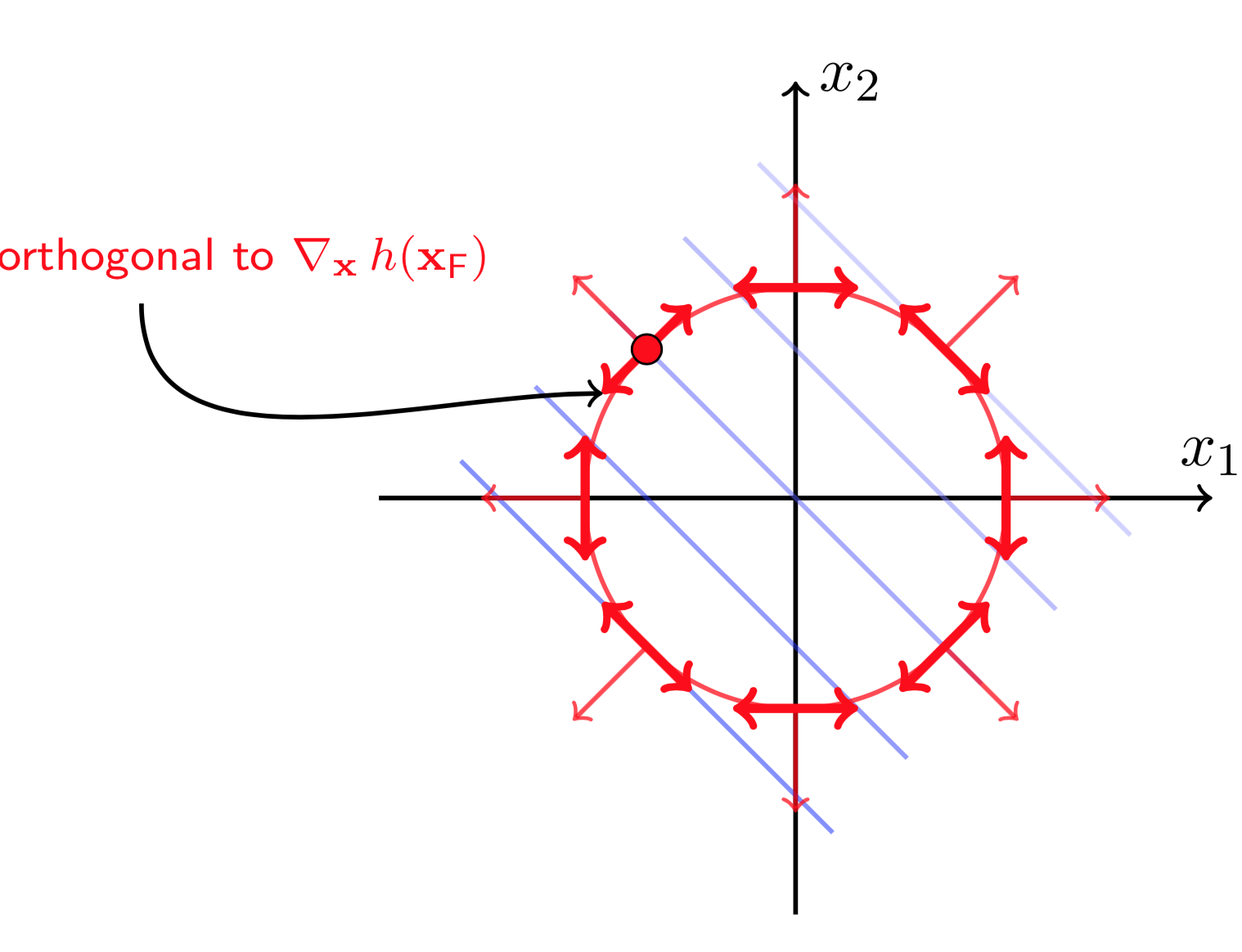
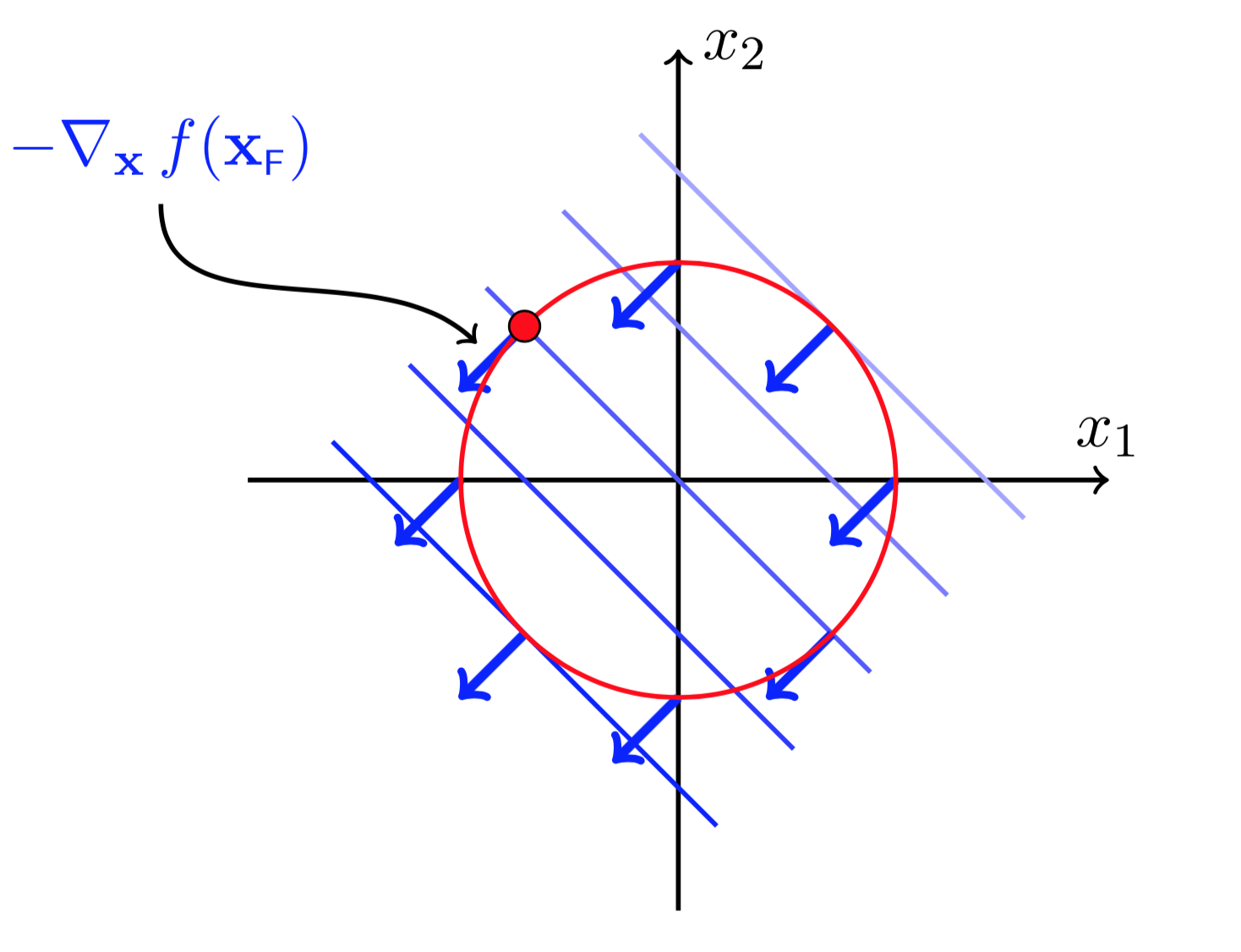
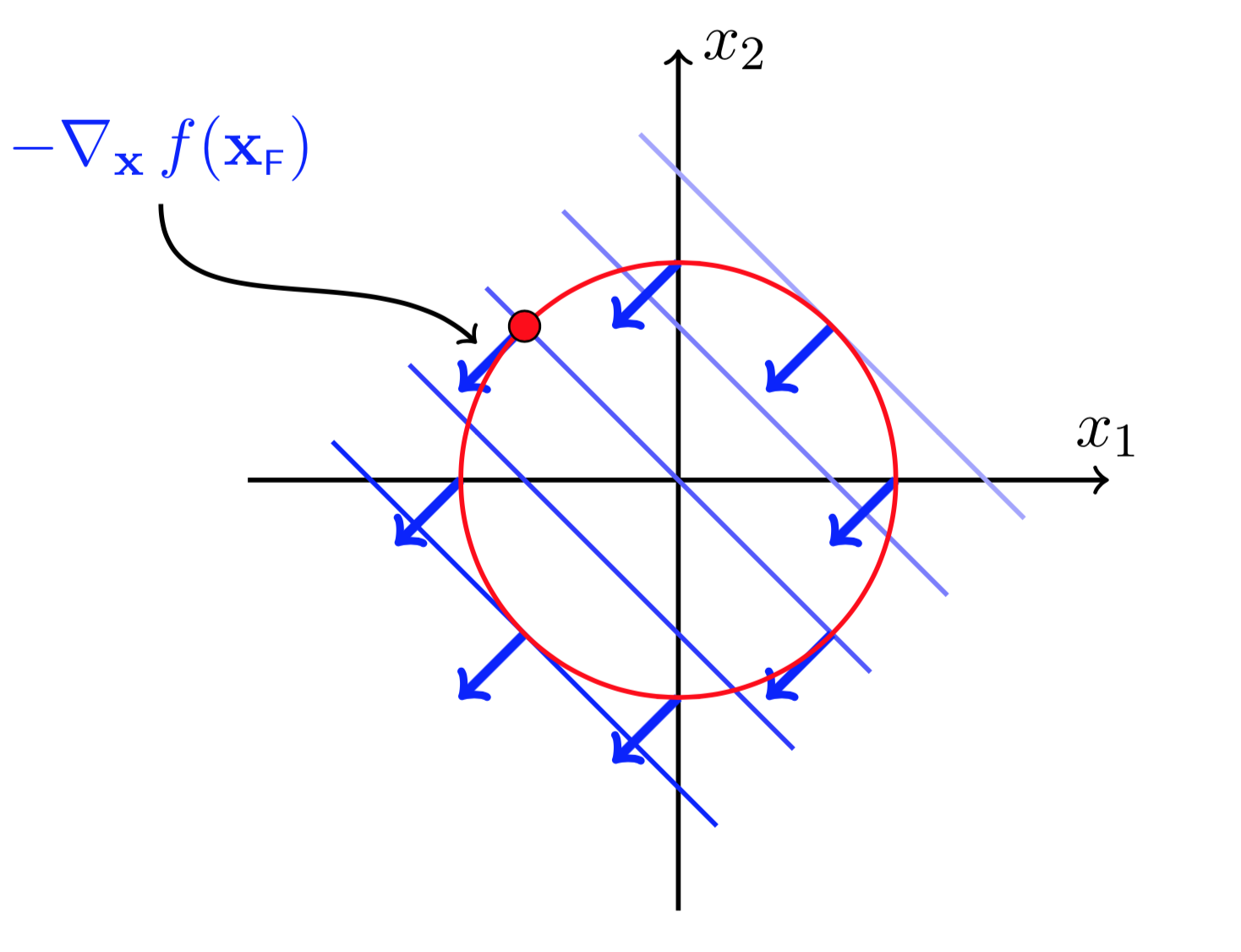
                              图（5 ）                                                        图（6）

图（5）和图（6）分别画出了约束函数\(h(X)\)的梯度方向以及梯度的正交方向。为了限制在移动\(X_F\)后，使得\(X_F+\Delta X\)依然在约束曲线上，则\(\Delta X\)必须沿着\(h(X)\)梯度的正交方向移动（否则\(h(X)\)会增大或减小，这样不再满足约束条件\(h(X)= 0\)）。这说明任何时刻都有

• \(\Delta X\)沿着\(\nabla_Xh(X_F)\)正交方向移动，可以保证\(h(X_F+\Delta X)=0\).

• 当$f(X_F) >f(X_F+ \Delta X) $时，必须有

  \[\Delta X \cdot (-\nabla_X f(X)) > 0 \]

考虑一种情况

\[\nabla_X f(X_F) = \mu \nabla_X h(X_F) \]

其中\(\mu\)是一个常数，此时

• 当移动\(\Delta X\)时，\(\Delta X \cdot (-\nabla_x f(X)) = -\mu\Delta X \cdot \nabla_x h(X) = 0\).
• 无法找到一个方向\(\Delta X\)使得\(f(X)\)能够继续减小或增大，此时\(X_F\)是函数的一个极值点.

回到我们最初的问题

\[\min_{X \in R^n} f(X) \quad s.t. \; h(X) = 0. \]

定义拉格朗日函数

\[L(X,\lambda) = f(X) +\lambda h(X) \]

\(X^*\)是一个局部最小值的充分条件是

• \(\nabla _XL(X^*,\mu^*) = 0\).
• \(\nabla _{\mu}L(X^*,\mu^*) = 0\).
• \(Y^T\nabla_{XX}^2L(X^*,\mu^*)Y>0 \quad s.t. \;(\nabla_Xh(X^*))^TY = 0\)

最后的约束条件是保证\(Y\)的方向与\(h(X)\)梯度方向正交。上面结论很容易推广到多等式约束问题，设

\[\min_{X \in R^n} f(X) \quad s.t. \; h_i(X) = 0 \quad i=1,2,...,l \]

定义拉格朗日函数

\[L(X,\lambda) = f(X) +\sum_{i=1}^l\mu_i h_i(X) = f(X)+\mu^Th(X) \]

\(X^*\)是一个局部最小值的充分条件是

• \(\nabla _XL(X^*,\mu^*) = 0\).
• \(\nabla _{\mu}L(X^*,\mu^*) = 0\).
• \(Y^T\nabla_{XX}^2L(X^*,\mu^*)Y>0 \quad s.t. \;(\nabla_Xh(X))^TY = 0\)

不等式约束条件

只包含一个不等式约束的优化问题

\[\min_{X \in R^n} f(X) \quad s.t. \; g(X) \leq 0. \]

为了便于理解，我们设

\[f(X) =x_1^2+x_2^2, \\ g(X)=x_1^2+x^2_2-1. \]

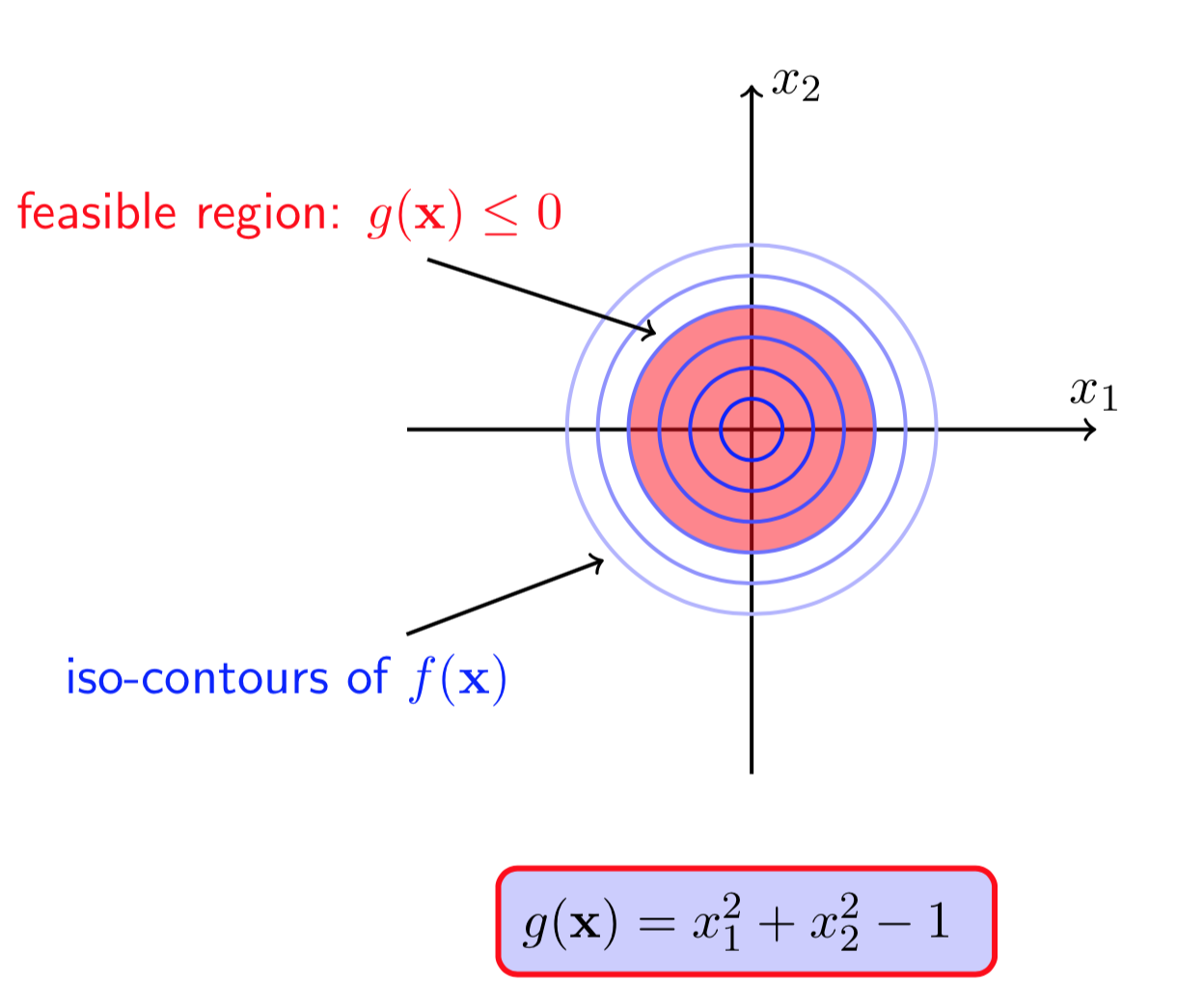
                              图（7 ）                                                        图（8）

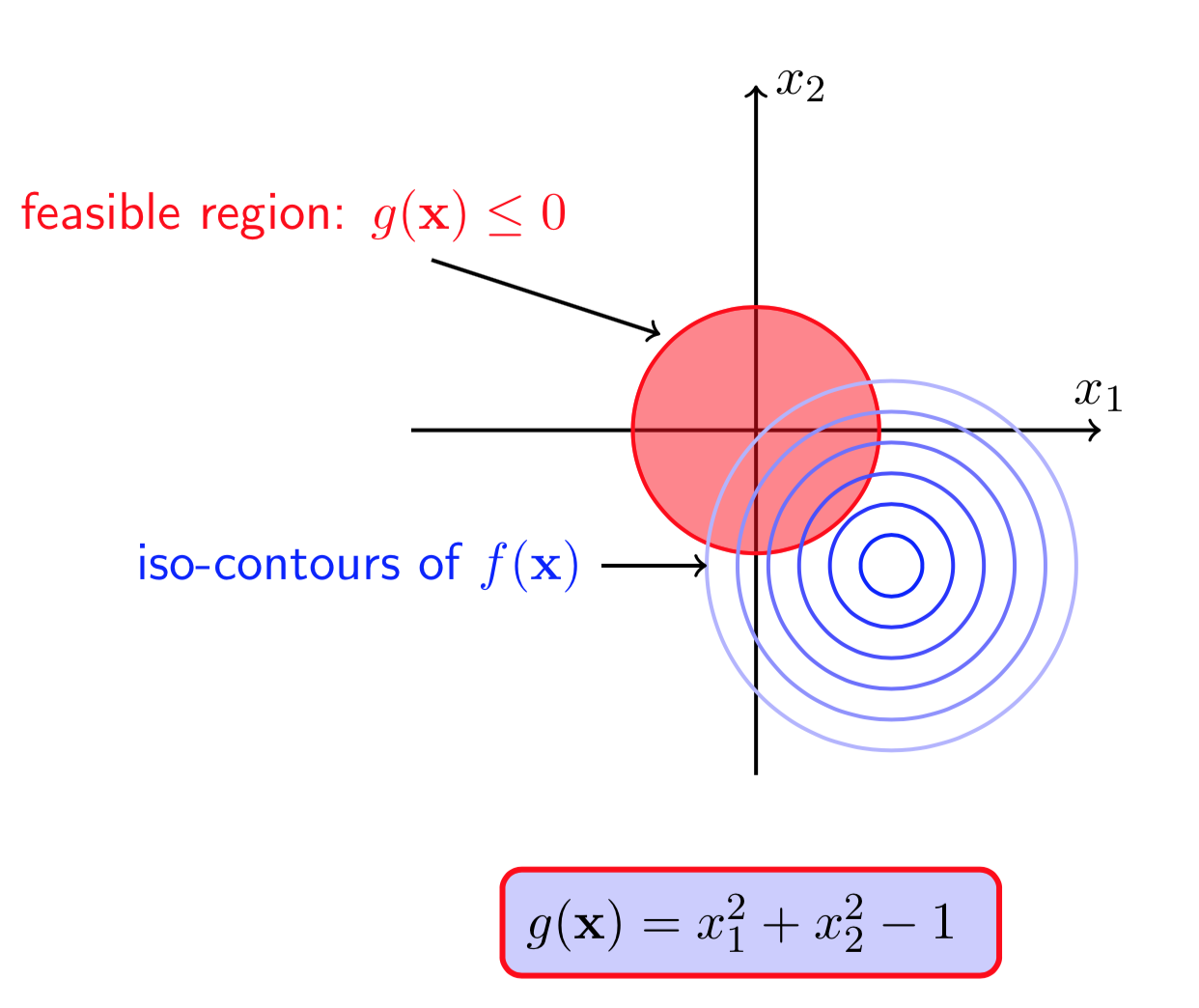
图（7）画出了\(f(X)\)的等高线，并且点\((0,0)\)是一个极小值点，图（8）的红色区域是在\(g(X)\)约束条件下的可行域。从图中可以看出，无论是否有\(g(X)\)的约束，函数\(f(X)\)的极小值点都在\((0,0)\)处，此时我们称该约束未被激活（\(g(X^*)<0\)）.现在，如果把目标函数修改成

\[f(X)=(x_1-1.1)^2+(x_2-1.1)^2 \]

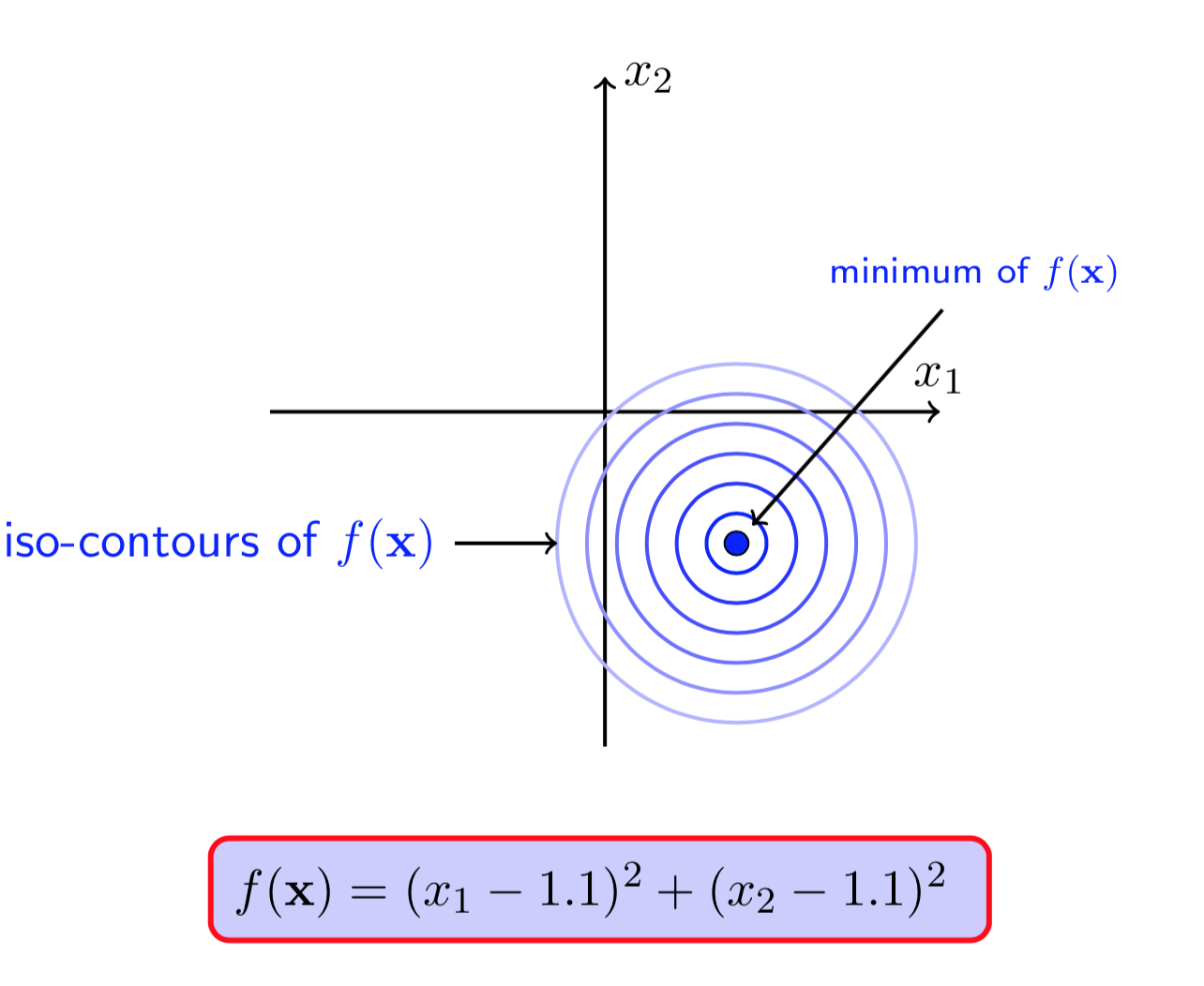
                              图（9 ）                                                        图（10）

图（9）和（10）显示，\(f(X)\)在无约束条件下的极值点是\((1.1,1.1)\),但是它并不在\(g(X)\leq0\)的可行域中。这种情况下，若\(X^*\)是\(f(X)\)满足约束条件的一个极小值点，那么一定有\(g(X^*)=0\),也即极小值点一定在约束的边界上取得。实际上，此处的不等式约束就变成了等式约束。

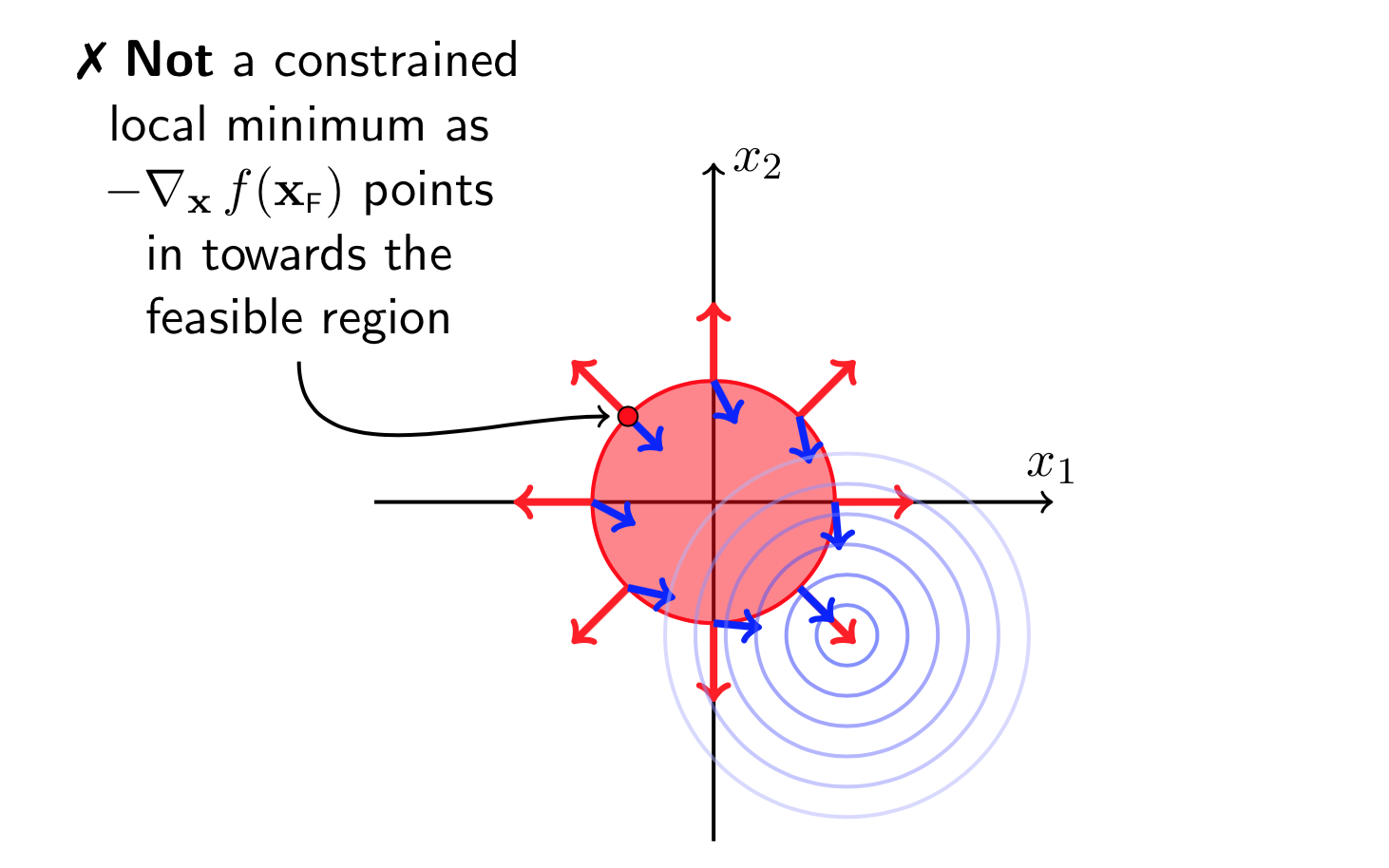
​ 图（11）

从图(11)可以看出来，在极小值点处\(-\nabla f(X)\)与\(\nabla g(X)\)的方向是一致的

\[-\nabla f(X) = \lambda \nabla g(X)\quad and \quad \lambda >0 \]

其实这也不难理解,如果说\(X^*\)是一个极小值点，上面分析知道\(g(X)\leq 0\)被激活，所以\(g(X^*)=0\),如果设从点\(X^*\)出发下一步可行的方向为\(\Delta X\)，由于要满足\(g(X^*+\Delta X) \leq 0\),所以

\[\Delta X \cdot \nabla g(X^*) \leq 0 \quad (1) \]

所以下一步的所有可行方向需要满足上述不等式约束，因为\(X^*\)是一个极小值点，也就是说沿着满足上式(1)的\(\Delta X\)的方向，都有$f(X^) \leq f(X^+\Delta X) $，也就是

\[\Delta X \cdot \nabla f(X^*) \geq 0 \quad (2) \]

并且我们知道\(X^*\)一定在\(g(X)=0\)上，通过上一节的等式约束的条件，应有

\[\nabla f(X^*) = \mu \nabla g(X^*) \quad (3) \]

通过\((1,2,3)\)式可知\(\mu \leq 0\)，从而\(\lambda = -\mu \geq 0\).

现在我们来总结一下上面讨论的结果，给出优化问题

\[\min_{X \in R^n} f(X) \quad s.t. \; g(X) \leq 0. \]

如果\(X^*\)是一个极小值点，则可能有一下两种情况：

• Case 1: 无约束条件的极小值点出现在可行域内
  • \(g(X^*) < 0\).
  • \(\nabla _X f(X^*) = 0\).
  • \(\nabla^2 _{XX}f(X)\)是一个正定矩阵.
• Case 2: 无约束条件的极小值点出现在可行域外
  • \(g(X^*)=0\).
  • \(-\nabla _Xf(X^*) = \lambda \nabla g(X^*) \quad where \quad \lambda > 0\).
  • \(Y^T\nabla_{XX}^2L(X^*)Y \geq 0 \quad s.t. \;(\nabla_Xg(X^*))^TY = 0\)

下面，直接引入\(KKT\)条件

\[\min_{X \in R^n} f(X) \quad s.t. \; g(X) \leq 0. \]

定义拉格朗日函数

\[L(X,\lambda) = f(X)+\lambda g(X). \]

\(X^*\)是一个局部最小值等价于存在唯一的\(\lambda^*\)满足

• KKT1 . \(\nabla _X L(X^*,\lambda^*)=0\).
• KKT2. \(\lambda ^* \geq 0\).
• KKT3. \(\lambda ^*g(X^*) = 0\).
• KKT4. \(g(X^*) \leq 0\).
• KKT5. 矩阵\(\nabla _{XX}L(X^*,\lambda ^*)\)正定.

上面就是\(KKT\)条件。这些条件其实可以分两种情况

• Case 1: 约束未激活
  • 此时\(\lambda ^* = 0,L(X^*,\lambda^*)=f(X^*)\),
  • KKT1 \(\Rightarrow \nabla _Xf(X^*)=0\).
  • KKT4 \(\Rightarrow X^*\)是一个可行点
• Case 2: 约束被激活
  • 此时\(\lambda ^* \geq 0,L(X^*,\lambda^*)=f(X^*)+\lambda ^*g(X^*)\),
  • KKT1 \(\Rightarrow \nabla _Xf(X^*) =- \lambda \nabla g(X^*)\).
  • KKT3 \(\Rightarrow g(X^*) = 0\).并且\(L(X^*,\lambda^*)=f(X^*)\).

将问题推广到多个不等式约束

\[\min_{X \in R^n} f(X) \quad s.t. \; g_i(X) \leq 0. \quad i =1,2,...,m \]

定义拉格朗日函数

\[L(X,\lambda) = f(X) +\sum_{i=1}^m\lambda_i g_i(X) = f(X)+\lambda^Tg(X) \]

\(X^*\)是一个局部最小值等价于存在唯一的\(\lambda^*\)满足

• KKT1 . \(\nabla _X L(X^*,\lambda^*)=0\).
• KKT2. \(\lambda _j^* \geq 0\quad j=1,2...,m\).
• KKT3. \(\lambda_j^*g_j(X^*) = 0 \quad j=1,2,...,m\).
• KKT4. \(g_j(X^*) \leq 0 \quad j=1,2,...,m\).
• KKT5. 矩阵\(\nabla _{XX}L(X^*,\lambda ^*)\)正定.

同时存在等式和不等式约束

我们回到最开始的情况，同时存在多个等式约束和多个不等式约束

\[\min_{X \in R^n}f(X) \quad s.t. \; g_i(X) \leq 0 \; , \;h_j(X) = 0 \quad, i =1,2,...,l \quad and \quad j =1,2,...,m \]

定义拉格朗日函数

\[L(X,\lambda) = f(X) +\sum_{j=1}^l\mu_j h_j(X)+\sum_{i=1}^m\lambda_i g_i(X) = f(X)+\mu^Th(X) +\lambda^Tg(X) \]

\(X^*\)是一个局部最小值等价于存在唯一的\(\lambda^*\)满足

• KKT1 . \(\nabla _X L(X^*,\mu^*,\lambda^*)=0\).
• KKT2. \(\lambda _j^* \geq 0\quad j=1,2,...,m\).
• KKT3. \(\lambda_j^*g_j(X^*) = 0 \quad j=1,2,...,m\).
• KKT4. \(g_j(X^*) \leq 0 \quad j=1,2,...,m\).
• KKT5. \(h_i(X^*) = 0 \quad i =1,2,...,l\)
• KKT6. 矩阵\(\nabla _{XX}L(X^*,\lambda ^*)\)正定.

下面通过一个例子来加深理解，考虑问题

\[\min \quad x_1^2+x_2^2 \\ s.t. \quad x_1+x_2 = 1. \\ x_2 \leq \alpha . \]

构造拉格朗日函数

\[L(x_1,x_2,\lambda, \mu) = x_1^2+x_2^2+\mu(x_1+x_2-1)+\lambda(x_2-\alpha) \]

KKT方程如下：

\[\nabla _xL=(2x_1+\mu,2x_2+\mu+\lambda) = 0,\\ x_1+x_2 = 1, \quad \quad\quad\quad\quad\quad\quad\quad\quad\\ x_2 \leq \alpha, \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\ \lambda \geq 0, \quad\quad\quad\quad\quad\quad\quad\quad \quad\quad\quad\;\;\\ \lambda(x_2-\alpha) =0.\quad\quad\quad\quad\quad \quad\quad\quad \]

联立得

\[\lambda \geq 2 - 4 \alpha \]

• 当\(\alpha \ge 1/2\)时，\(\lambda = 0 \geq 2 -4 \alpha\),此时约束条件未被激活，原问题的最优解为\((x_1,x_2)=(1/2,1/2)\).
• 当\(\alpha < 1/2\)时，\(\lambda = 2 - 4\alpha > 0\)，从而\(x_2-\alpha = 0\),即\(x_2=\alpha\),此时约束条件被激活，愿问题最优解为\((x_1,x_2)=(1-\alpha,\alpha)\).