（原创）机器学习之矩阵论（三）

矩阵求导

目录

一、  矩阵求导的基本概念

1.    一阶导定义

2.    二阶导数

二、  梯度下降

1.   方向导数.

1.1 定义

1.2 方向导数的计算公式.

1.3 梯度下降最快的方向

1.4 最速下降方向的判断.

1.5 最速梯度下降的迭代式

2.   牛顿法

2.1 引入一元函数极值判别法

（1）导数分析法

（2）泰勒公式法

2.2 多元函数的泰勒展开

2.3  正定(半正定)矩阵

（1）二次型

（2）正定(半正定)的定义

（3）负定(半负定)的定义

（4）正定判别极值

2.4 正定矩阵的判别法

（1）根据特征值判断

（2）根据各阶顺序主子式判断

（3）判别正定的作用

三、矩阵求导的应用

1.  最小二乘法（线性回归）

1.1 一维模型

1.2 高维模型.

1.3 用SVD处理岭回归

2. Logistic回归

2.1 模型

2.2  最小化目标函数

 

一、矩阵求导的基本概念

多元函数极值问题，需要用到多元函数的导数，在矩阵理论里，又称为矩阵求导。

1.  一阶导定义

　　设：

　　　　𝑓: 𝑅^𝑛 → 𝑅

　　为一个n元一阶可微函数 𝑦 = 𝑓(𝑥₁, …, 𝑥_𝑛)，

　　定义其梯度(一阶导)向量为:

　　　　𝛻𝑓(𝑥) = ( 𝜕𝑥₁𝑓, 𝜕𝑥₂𝑓, …, 𝜕𝑥_𝑛𝑓)

　　或者：

　　　　𝛻_𝒙𝑓(𝒙) = ( 𝜕𝑥₁𝑓, 𝜕𝑥₂𝑓, …, 𝜕𝑥_𝑛𝑓)

　　其中𝒙 = 𝑥₁, 𝑥₂, …, 𝑥_𝑛

2.  二阶导数

　　二阶导数也称为Hessian矩阵：

                       

　　其中𝑎_𝑖𝑗 = 𝜕𝑥_𝑖𝑥_𝑗𝑓

　　注： 由于𝜕𝑥_𝑖𝑥_𝑗𝑓 = 𝜕𝑥_𝑗𝑥_𝑖𝑓，所以𝑎_𝑖𝑗=𝑎_𝑗𝑖，所以𝐻𝑓=𝐻𝑓^𝑇，即𝐻𝑓是n x n的实对称矩阵。

二、梯度下降

1.   方向导数

1.1 定义

　　设单位向量𝒖是𝑅^𝑛中的一个方向，n元函数𝑓(𝑥₀)沿𝒖方向的斜率，称为为𝑓(𝑥₀)在𝒖方向的方向导数。

1.2  方向导数的计算公式

              𝜕_𝒖 𝑓(𝑥₀) = 𝒖∙𝛻_𝒙 𝑓(𝑥₀)^𝑇

        即：方向导数 = 单位向量𝒖和梯度向量的内积。

1.3  梯度下降最快的方向

       由方向导数的内积计算公式有：

              𝒖∙𝛻_𝒙 𝑓(𝑥₀)^𝑇 = |𝒖| | 𝛻_𝒙 𝑓(𝑥₀)^𝑇 | cos𝜃

        |𝒖| = 1, | 𝛻_𝒙 𝑓(𝑥₀)^𝑇 |与𝒖无关。

　　因此，当𝜃=0时，方向导数＞0，取得最大值；当𝜃=𝜋时，方向导数＜0，取得最小值。

1.4  最速下降方向的判断

　　对于函数𝑓(𝒙)中的任意一点𝒙∈𝑅^𝑛，沿着和梯度向量一样的方向时，函数递增最快；沿着和梯 度向量相反方向时，函数递减最快。因此最速下降方向为−𝛻𝑓(𝒙)。

1.5 最速梯度下降的迭代式

　　𝒙(𝑡+1) = 𝒙(𝑡) – k∙𝛻𝑓(𝒙_𝒕)  k为控制下降速度的常数

2.   牛顿法

2.1  引入一元函数极值判别法

（1） 导数分析法

　　若𝑓’(𝑥₀) = 0，且𝑓’’(𝑥₀) ＞ 0，则𝑓(𝑥)在𝑥 = 𝑥₀处取极小值；

　　若𝑓’(𝑥₀) = 0，且𝑓’’(𝑥₀) ＜ 0，则𝑓(𝑥)在𝑥 = 𝑥₀处取极大值。

（2） 泰勒公式法

　　𝑓(𝑥) = 𝑓(𝑥) + 𝑓’(𝑥₀)(𝑥−𝑥₀) + (1/2) 𝑓’’(ξ)(𝑥−𝑥₀)²

　　       = 𝑓(𝑥) + (1/2) 𝑓’’(ξ)(𝑥−𝑥₀)²               ( ξ为(𝑥，𝑥₀)或(𝑥₀，𝑥)  )

　　当𝑓’’(𝑥₀) ＞ 0时，由导数的保号性，在𝑥₀很小的邻域内有𝑓’’(ξ) > 0，因此在𝑥₀的邻域内恒有𝑓(𝑥)  > 𝑓(𝑥₀)，即函数𝑓(𝑥)在𝑥 = 𝑥₀处取极小值。

2.2 多元函数的泰勒展开

 　　

　　其中𝐻𝑓为Hessian矩阵，如果𝒙₀点满足𝛻𝑓(𝒙₀) = 𝜽(零向量)，则

　　(𝒙−𝒙_𝟎)𝐻𝑓(𝒙₀)(𝒙−𝒙_𝟎)^𝑇  ＞ 0，函数𝑓(𝒙)在𝒙=𝒙₀处取得极小值；

　　(𝒙−𝒙_𝟎)𝐻𝑓(𝒙₀)(𝒙−𝒙_𝟎)^𝑇  ＜ 0，函数𝑓(𝒙)在𝒙=𝒙₀处取得极大值；

2.3 正定(半正定)矩阵

（1）二次型

　　A是一个n阶对称矩阵，即𝐴 = 𝐴^𝑇（𝑎_𝑖𝑗=𝑎_𝑗𝑖），设n维向量x = (𝑥₁, 𝑥₂, …, 𝑥_𝑛)，定义:

 　　　　

　　为A对应的二次型（或称二次型多项式），方阵A为二次型对应的矩阵。

（2）正定(半正定)的定义

　　若任意的x≠𝜽，都有：

　　　　𝑓(𝑥₁,𝑥₂,…,𝑥_𝑛) = 𝒙𝐴𝒙^𝑇 ＞ 0（≤0），

　　则称该二次型为正定（半正定）二次型，对应的矩阵A为正定（半正定）矩阵。

（3）负定(半负定)的定义

　　若任意的x≠𝜽，都有：

　　　　𝑓(𝑥₁,𝑥₂,…,𝑥_𝑛) = 𝒙𝐴𝒙^𝑇 ＜ 0（≥0），

　　则称该二次型为负定（半负定）二次型，对应的矩阵A为负定（半负定）矩阵。

（4）正定判别极值

　　如果在𝒙=𝒙₀处，有𝛻𝑓(𝒙₀) = 𝜽(零向量)，我们称𝒙₀为𝑓(𝒙)的驻点:

　　i）   如果𝐻𝑓(𝒙₀)正定矩阵，𝑓(𝒙)在𝒙 = 𝒙₀处是一个局部极小值

　　ii）  如果𝐻𝑓(𝒙₀)负定矩阵，𝑓(𝒙)在𝒙 = 𝒙₀处是一个局部极大值

　　iii） 如果𝐻𝑓(𝒙₀)不定矩阵，𝑓(𝒙)在𝒙 = 𝒙₀处没有极值

2.4  正定矩阵的判别法

（1）根据特征值判断

       1）引理

　　　　对称方阵一定可以正交分解（正交对角化），即任意的对称矩阵A，必然存在一个正交矩阵Q，使得：

　　　　 

2）进行判别

              上述正交分解的式子进行换元，设𝒙𝑄 = 𝒚 = (𝑦₁, 𝑦₂, …, 𝑦_𝑛)，则有：

　　　　　　 

              A的每一个特征值𝜆_𝑖＞0(≥0)，则二次型𝑓(𝑥₁,𝑥₂,…,𝑥_𝑛) = 𝒙𝐴𝒙^𝑇正定（半正定），反之也成立。

（2）根据各阶顺序主子式判断

       对称矩阵正定的充分必要条件是A的各阶顺序主子式（各阶子式的行列式）为正数，即：

　　　　 

（3）判别正定的作用

　　1）多元函数的极值问题，可以通过求驻点处的Hessian矩阵是否正定来解决。

　　2）使用计算机编程来判定矩阵是否正定时，一般通过各阶顺序主子式来进行判断，因为行列式在使用计算机进行计算时是绝对精确的，而特征值的求解是通过逼近的方式进行计算的，时间复杂度较大，精度较差。

三、矩阵求导的应用

1. 最小二乘法（线性回归）

1.1 一维模型

       对于一维线性回归模型，假设有样本点(𝑥_𝑖,𝑦_𝑖) (𝑖=1,2,…,𝑚)，线性回归就是选择最佳的a，b值使：

              𝑓(𝑥_𝑖) = 𝑎𝑥_𝑖 + 𝑏

　　满足 𝑓(𝑥_𝑖) ≈ 𝑦_𝑖 （理论值最接近实际值）

　　即求：

　　　　

              求梯度：

 　　　　　　 

　　并且Hessian矩阵是正定的，说明此时的a，b使得L2范数局部最小(在这里也是全局最小)。

1.2 高维模型

　　对于高维线性回归模型，假设有样本点(𝑥_𝑖, 𝑦_𝑖) (𝑖=1,2,…,𝑚)，其中𝒙_𝒊∈𝑅^𝑛, 𝑦_𝑖∈𝑅

　　找到最佳的 𝒂∈𝑅^𝑛, 𝑏∈𝑅 使：

              𝑓(𝑥_𝑖) = 𝑎𝑥_𝑖 + 𝑏

　　满足 𝑓(𝑥_𝑖) ≈ 𝑦_𝑖 （理论值最接近实际值）

　　其中，

 　　　　

　　写成矩阵的形式：

 　　　　

　　即求：

 　　　　

　　最小。

　　求梯度：

 　　　　

　　并且Hessian矩阵是正定的，说明此时的𝝎使得L2范数局部最小，𝝎为最优值。

       如果𝐴^𝑇𝐴不可逆怎么办？使用岭回归。

1.3 用SVD处理岭回归

       如果矩阵𝐴^𝑇𝐴不可逆，则用岭回归代替线性回归。

　　线性回归：

 　　　　

　　岭回归：

 　　　　

　　岭回归性质：损失无偏性(无偏：估计出来的期望=实际的期望)，增加稳定性，从而得到较高的计算精度。

　　　

2. Logistic回归

2.1 模型

　　变量𝒙 = (𝑥_𝟏, 𝑥₂, …, 𝑥_𝑛)，满足线性组合函数:

　　　　g(𝒙) = 𝜔₀ + 𝜔₁𝑥₁ + ⋯ + 𝜔_𝑛𝑥_𝑛

　　概率模型满足sigmoid函数:

 　　　　

       观测到m个样本数据(𝒙₁, 𝑦₁), (𝒙₂, 𝑦₂), …, (𝒙_𝑚, 𝑦_𝑚)，其极大似然函数为：

             

2.2  最小化目标函数

　　对目标函数（极大似然函数）

 　　　　

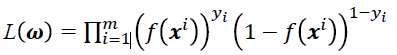
       左右同时取对数有：

             　

　　求其梯度，并令𝛻𝑙𝑛𝐿(𝝎) = 𝜃，得到方程组：

     　　　

　　解此方程组得到的𝝎即为最优权重。

　　　　

　　　　　　- tany 2017年10月4日于杭州

 

人工智能从入门到专家教程资料：https://item.taobao.com/item.htm?spm=a1z38n.10677092.0.0.38270209gU11fS&id=562189023765