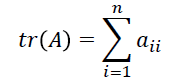(原创)机器学习之矩阵论(一)
目录
一、向量运算
1. 加法
2. 数乘
3. 内积
二、矩阵
1. 何为线性?
2. 矩阵的定义
3.矩阵的作用
4. 矩阵的本质
5. 特殊的矩阵
6. 矩阵和向量的关系
二、矩阵的基本运算
1. 矩阵相等
2. 矩阵加法
3.矩阵数乘运算
4.矩阵与矩阵的乘法
5.矩阵的转置
6.方阵的行列式
7.矩阵的逆
8.矩阵的秩
9.矩阵的迹
一、向量运算
假设x, y![]() R2,即x=(x1, x2),y=(y1,y2)
R2,即x=(x1, x2),y=(y1,y2)
1. 加法:𝒙+𝒚 = (𝑥1+𝑦1, 𝑥2+𝑦2)
2. 数乘: 𝑎𝒙 = (𝑎𝑥1, 𝑎𝑥2)
3. 内积: 𝒙𝒚 = 𝑥1𝑦1 + 𝑥2𝑦2
二、矩阵
1. 何为线性?
数乘和加法统称为线性。
2. 矩阵的定义:
由 m×n 个数𝑎𝑖𝑗(𝑖=1,2,..,𝑚; 𝑗=1,2,…,𝑛), 排成的 m 行、n 列的数表:
称为 m 行 n 列矩阵,简称 m×n 矩阵,常用大写字母表示,记作𝐴、𝐴𝑚×𝑛或者(𝑎𝑖𝑗)𝑚×𝑛,
其中𝑎𝑖𝑗为矩阵第 i 行、第 j 列的元素。
3.矩阵的作用:
统一表示线性方程和线性变换,方便处理线性方程和线性变换的问题。研究矩阵的算法和性质,即研究了线性方程和线性变换的性质。
4. 矩阵的本质:
矩阵是线性方程组系数的一种简化表示。
矩阵,英文单词:matrix,母体的意思,说明矩阵就是线性方程的母体,即主体部分。
5. 特殊的矩阵
(1)方阵:行数和列数都等于n的矩阵,记作An。
(2)单位矩阵:对角线上元素为1,其余为0的方阵,记作In或者En。
(3)对角矩阵:只有对角线上有元素,其余为0的方阵,简称对角阵,记作
A =diag (a1,a2,…an,) 或者 Λ =diag (λ1,λ2,…,λn)
(4)零矩阵:元素全为0的矩阵,记作0或者0m×n。
(5)三角矩阵:只有对角线以上(下)有元素,其余为0的矩阵,称为上(下)三角矩阵。
6. 矩阵和向量的关系:向量包含与矩阵,向量是矩阵的一部分。
(1)n元行向量可以看成1行n列的矩阵。
(2)n元列向量可以看成n行1列的矩阵。
(3)n行m列的矩阵可以表示为n行m元行向量构成。
(4)n行m列的矩阵可以表示为m列n元列向量构成。
二、矩阵的基本运算
1. 矩阵相等:
如果两个矩阵的行数和列数相等,并且对应的每个元素都相等,则这两个矩阵相等,记作A =B。
注意:不同阶数的矩阵是不同等的。
2.矩阵加法:
注意:
(1)具有相同行数和列数的矩阵才能相加。
(2)矩阵的加法是2个同型矩阵对应位置上的元素相加。
(3)矩阵没有减法,矩阵相减通过矩阵加上一个负矩阵来实现,等于2个同型矩阵对应位置上的元素相减。
(4)矩阵加法的运算规律:
1)结合律:A + ( B + C ) = ( A + B ) + C
2)交换律:A + B = B + A
3)零矩阵运算:A + O = A;A + ( - A ) = O;
3.矩阵数乘运算
设k为实数,A = ( aij )为矩阵,称矩阵为数与矩阵的乘积,简称数乘运算,记为kA= (kaij)。
(1)运算规律:
1) 1 A = A ,
2) ( k + l ) A = kA + lA ,
3) k (A + B ) = kA + kB ,
4) k ( lA ) = ( kl ) A ,
4.矩阵与矩阵的乘法
(1)为什么矩阵相乘不能像矩阵加法和数乘一样对应位置元素进行运算即可?
使用方程组来解释:
1) 矩阵加法和数乘对应的就是线性系统之间的加法和数乘。
2) 两个矩阵间对应位置元素相乘没有意义,并且相乘之后线性系统等号不再成立。
(2)矩阵相乘定义:
设 A = ( aij )m×s , B = ( bij )s×n ,那么规定矩阵C = ( cij )m×n:
称为A与B的乘积,或A左乘B(B右乘A),记为C = AB。
即:
乘积矩阵的第i行第j列的元素 = 左矩阵的第i行向量与右矩阵的第j列向量做内积。
注意:
1) 只有当左矩阵的列数 = 右矩阵的行数时,两个矩阵才能相乘,Cm×n = AmxsBsxn。
2) 矩阵乘法不满足交换律:AB不一定等于BA。
3) 两个非零矩阵的乘积可能是零矩阵。
(3)运算规律:
1) 结合律:( AB )C = A( BC );
2) 分配律:A( B + C ) = AB + AC, ( B + C ) A = BA + CA;
3) k ( AB )= ( kA ) B (其中 k 为实数),
4) 单位矩阵满足交换律:InAn=AnIn=An
(4)从本质上来讲:
矩阵是一个线性变换,矩阵乘法就是一个复合,就是求复合函数的变换。
5.矩阵的转置
为矩阵 A的转置,记作 AT,( aijT= aji),即,
把行向量变成了列向量。(形式变了,但是本质没有变,只是为了便于计算)。
运算规律:
(1)( AT )T = A
(2)( A + B )T = AT + BT
(3)( k A )T = k AT
(4)( AB )T = BTAT
6.方阵的行列式
行列式英文单词determine,意思是决定因子,说明它将决定矩阵的一些性质(决定线性方程组是否有唯一解),行列式记作:det(A)或者|A|.
(1)行列式的性质
1) 只有方阵才可以定义行列式。
2) 如果A是对角阵或者三角阵,|A|为对角线的乘积,比如|In|=1
3) |kAn|=kn|An|
4) AB和BA不一定相等,但是|AB|=|BA|=|A||B|
(2)行列式的应用:克莱默(Cramer)法则:
如果线性方程组
的系数矩阵的行列式不等于零,即
则线性方程组(1)有唯一解。其解为:
其中
即Dj是把系数矩阵行列式D中的第j列的元素替换成方程组右端的常数项的列向量,所得到的n阶行列式。
7.矩阵的逆A-1
(1)逆矩阵的定义
设A为n阶方阵,如果有n阶方阵B,使得
AB = BA = In
则称A为可逆矩阵,B为A的逆阵,记作B=A-1。(只要AB = In,必然有BA =In )
(2)逆矩阵的性质
1)(A−1)−1=A
2)(kA)−1=(1/k)A−1 (k≠0)
3)A、B 均是同阶可逆阵,则(AB)−1=B−1A−1
4)转置和逆可交换,即(A−1)T=(AT)−1
8.矩阵的秩
秩,英文单词rank,意思是阶,等级的意思,说明秩就是矩阵的阶数。
(1)矩阵的初等行(列)变换:
1)对换两行(列)的位置;
2)将常数 k (k≠0) 乘以某行(列)向量;
3)将某行(列)的元素乘上倍加到另一个行(列)上
经过初等变换之后,矩阵变了但是其代表的线性系统没有变。
(2)秩的定义:
对于任一矩阵 A,经过初等变换可以把它变成
这里,r 是由 A 唯一决定的. 这个 r 称为矩阵的秩
(3)秩的求法:
只用初等行(列)变换把矩阵A化为阶梯矩阵,阶梯矩阵中不为0向量的行(列)数为矩阵A的秩。
(4)行秩、列秩
用行变换得到的秩称为行秩;用列变换得到的秩称为列秩;行秩 = 列秩
(5)秩的本质:
矩阵在其等价的线性变换(初等变换)中,本质(无法被消去)的部分,即
可认为秩是线性方程组有r个未知变量(列秩)或r个方程(行秩)。(于是决定着方程组是否有唯一解)。
(6)秩的性质
1)零矩阵的秩是0
2)如果Am×n, 则R(A) ≤m, R(A) ≤n, 0 ≤R(A) ≤min { m , n }
3)r(AB)≤{r(A), r (B)} (越相乘秩可能越小)
4)如果A可逆,那么r(B)=r(AB)
5) 如果A是n阶方阵,
A的行列式不等于零,说明线性方程组有唯一解,说明线性方程组的系数矩阵A满秩,说明A可逆。
9.矩阵的迹
(1)定义:方阵A的对角线之和,称为迹,记作tr(A), 即
(2)运算性质
1)矩阵的迹 = 该矩阵的特征值之和
2)tr(AB) = tr(BA)
- tany 2017年10月2日于杭州
人工智能从入门到专家教程资料:https://item.taobao.com/item.htm?spm=a1z38n.10677092.0.0.38270209gU11fS&id=562189023765




![clip_image002[12]_thumb[2] clip_image002[12]_thumb[2]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002442224-962387151.png)
![clip_image005[10]_thumb[1] clip_image005[10]_thumb[1]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002443583-958259089.png)
![clip_image007[10]_thumb clip_image007[10]_thumb](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002444083-1170869928.jpg)
![clip_image008_thumb[2] clip_image008_thumb[2]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002444536-1560860046.png)
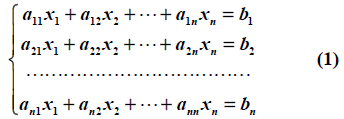
![clip_image010_thumb[2] clip_image010_thumb[2]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002445458-156112676.png)
![clip_image011_thumb[3] clip_image011_thumb[3]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002445849-841002150.png)
![clip_image012_thumb[2] clip_image012_thumb[2]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002446271-562054534.png)
![clip_image013_thumb[1] clip_image013_thumb[1]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002446755-1231366476.png)
![clip_image014_thumb[4] clip_image014_thumb[4]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171003002447255-156705244.png)