ds_c02 线性表
2.1 线性表的逻辑结构及相关概念
-
线性表的定义:线性表是具有相同数据类型的
-
线性表的特点:
- 表中元素个数有限;
- 表中元素具有逻辑上的顺序性,有先后次序;
- 表中元素的数据类型相同,这意味着每个元素占有相同大小的存储空间;
-
线性表的基本操作:
操作名 操作 插入 在指定位置插入一个新元素 删除 删除指定位置的元素 查找 查找特定值的元素,返回其位置 访问 获取指定位置的元素的值 遍历 顺序访问每个元素,以执行某种操作 判空 判断线性表是否为空,为空,返回 构造 构造一个的线性表 销毁 回收线性表
2.2 线性表的顺序存储方式——顺序表
线性表的顺序存储又称顺序表。它是用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理位置上也相邻。第
顺序表的特性造就了其随机存取的特性,这是顺序表最大的优势之一,即我们可以根据下标访问元素的值。
2.2.1 静态分配的顺序表的实现
const int Maxsize = 100; // 线性表的最大长度
typedef int ElemType;
struct SeqList {
ElemType data[Maxsize]; // 用数组存储线性表中的元素
int length; // 线性表的表长
// 构造函数,用于初始化线性表
SeqList():length(0) {}
};
int main()
{
SeqList L; // 自动调用构造函数进行初始化
}
ElemType表示抽象数据类型,说明线性表中的元素可以是已有的int、float等,也可以是自定义的数据类型,比如线性表中的元素可以为我们自己定义的线性表seqList
接下来是线性表的插入、删除、查找、访问、遍历、判空和销毁。首先是插入,初始化后得到的是一个空表,要往里面插入元素,才能使得表有意义,
bool insertList(SeqList &L, int index, ElemType element) {
// 检查插入位置的合法性,1 <= index <= length + 1,L.length < Maxsize
if (index < 1 || index > L.length + 1 || L.length >= Maxsize)
return false;
// 往后移动元素,为新元素腾出空间
for (int i = L.length; i >= index; i --)
L.data[i] = L.data[i-1];
// 插入元素,更新线性表的长度
L.data[index - 1] = element;
L.length ++;
return true;
}
- 时间复杂度:
- 顺序表的插入操作在实现上相对简单,但因为可能需要移动大量元素,其性能可能会受到影响,特别是当线性表长度较大时。在设计程序时,如果预期需要频繁执行插入操作,可能需要考虑使用其他数据结构(如链表),以提高效率。
想要知道元素有没有插入成功,除了判断 insertList 的返回结果是否为
void printList(const SeqList &L) {
for (int i = 0; i < L.length; ++i)
cout << L.data[i] << ' ';
cout << endl;
}
与插入操作相反的是删除操作,实现如下:
bool delList(SeqList &L, int index) {
// 检查删除位置的合法性,1 <= index <= length
if (index < 1 || index > L.length)
return false;
// [index, length-1]向前移动一位,填补空位
for (int i = index; i < L.length; ++i)
L.data[i-1] = L.data[i];
// 更新线性表的长度
L.length --;
return true;
}
- 时间复杂度:
- 顺序表的删除操作虽然在实现上直接,但与插入操作类似,可能需要移动大量元素,特别是在表的前端进行删除时。这可能会对性能产生显著影响,尤其是在表长度较大时。因此,在设计需要频繁删除操作的程序时,考虑使用链表等其他数据结构可能会更有效,因为链表的删除操作可以在
接下来是剩余的一些操作,查找和判空。
// 查找
int locateElement(const SeqList &L, ElemType element) {
for (int i = 0; i < L.length; ++i)
if (L.data[i] == element)
return i + 1; // 返回元素的位置,从 1 开始计数
return -1;
}
// 判空
bool isEmpty(const SeqList &L) {
return L.length == 0;
}
- 查找操作的时间复杂度:
- 判空操作的时间复杂度和空间复杂度都为
访问可以可以通过数组下标直接实现;销毁,顺序表是静态数组实现的,静态数组的内存分配在栈上,由编译器自动管理,不需要手动释放,所以不需要实现销毁操作。动态数组,内存分配在堆上,程序员必须手动管理内存。
2.2.2 动态分配的顺序表的实现
要将静态分配的顺序表修改为动态分配的顺序表,我们需要做的改动虽小,但这些改动会对数据结构的管理方式产生根本性的影响。基本的变更是将固定大小的数组 data 替换为一个指向动态分配数组的指针。变量名和结构体名保持不变,这样可以确保对现有代码的影响最小。
const int Maxsize = 100; // 定义线性表的最大长度
typedef int ElemType;
struct SeqList {
ElemType *data; // 指向动态分配的数组的指针
int length; // 线性表的当前长度
int capacity; // 线性表的容量
// 构造函数,用于初始化线性表
SeqList():length(0), capacity(Maxsize) {
data = new int[capacity];
cout << "Init success.\n";
}
// 析构函数,用于释放动态分配的函数
// 超出作用域后会自动调用
~SeqList() {
delete[] data;
}
};
使用动态分配的一个好处就是可以容量不够时,可以动态扩容,只需要在结构体中加入扩容函数,在执行插入操作的时,如果发现容量不够,调用扩容函数就可扩大容量。
下面代码中,扩容的基本逻辑是:申请一块现有容量两倍的空间,将原来的信息复制到这个新的空间中并释放原有的空间。具体实现如下:
const int Maxsize = 1; // 定义线性表的最大长度
typedef int ElemType;
struct SeqList {
ElemType *data; // 指向动态分配的数组的指针
int length; // 线性表的当前长度
int capacity; // 线性表的容量
// 构造函数,用于初始化线性表
SeqList():length(0), capacity(Maxsize) {
data = new int[capacity];
cout << "Init success.\n";
}
// 析构函数,用于释放动态分配的函数
// 超出作用域后会自动调用
~SeqList() {
delete[] data;
}
// 动态扩容
void doubleSpace() {
capacity *= 2; // 容量加倍
int *newdata = new int[capacity]; // 申请更大的空间
for (int i = 0; i < length; ++i) // 复制旧的内容
newdata[i] = data[i];
delete[] data; // 释放旧空间
data = newdata; // 更新指针,指向新的空间
cout << "add double space.\n";
}
};
除了以上两点,以及插入时可以扩容,与静态分配的代码相比,动态分配几乎没有什么改变。完整的动态分配代码实现。
2.2.3 静态分配和动态分配的比较
静态分配的顺序表和动态分配的顺序表在功能上都能实现相同的操作,但是它们在灵活性、内存管理和应用场景上有显著的差异。并不是说动态分配就一定好于静态分配,它们在不同的应用场景中具有不同的优缺点。
- 固定容量
- 静态分配:静态分配的顺序表使用固定大小的数组来存储元素。这意味着一旦定义,表的最大容量就固定了,不能根据需要进行扩展或缩减。这限制了表的使用,可能会导致空间浪费或空间不足
- 动态分配:动态分配的顺序表通常使用指针和动态内存分配(如
new或delete),可以根据需要扩展或缩减容量。这提供了更大的灵活性,可以优化内存使用,避免空间浪费。
- 内存利用
- 静态分配:静态分配可能导致内存浪费,因为分配的内存大小固定。如果元素数量远小于数组的最大容量,那么未使用的部分就浪费了。
- 动态分配:动态分配可以更加精确地控制内存使用,仅在需要时分配额外内存,从而更有效地利用资源。
- 实现复杂性
- 静态分配:从实现角度看,静态分配的顺序表较为简单。不需要管理内存分配和释放的复杂性,适合对性能要求不高且数据规模固定的场景。
- 动态分配:虽然动态分配提供了更多的灵活性和效率,但它也增加了实现的复杂性。开发者需要处理内存的动态分配和释放,这可能导致错误,如内存泄漏和指针误用。
- 性能考量
- 静态分配:在预先知道最大元素数量且数量不会变化的情况下,静态分配的顺序表性能较好,因为内存位置固定,访问速度快。
- 动态分配:虽然动态分配提供灵活性,但频繁的内存分配和释放可能影响性能,特别是在元素不断添加和删除的情况下。
- 存储位置:堆
- 静态分配:静态分配的顺序表通常使用栈内存(尤其是当顺序表作为局部变量定义时)。栈内存的分配和回收速度非常快,由操作系统自动管理。但栈的大小有限,且受到严格的局部作用域控制,超出作用域后立即被回收。这意味着静态分配的顺序表在局部作用域中非常高效,但不适用于需要大量数据或跨多个作用域存活的场景。
- 动态分配:动态分配的顺序表通常使用堆内存。堆内存提供了更大的灵活性和更长的生命周期。数据可以在堆上持续存放,直到显式释放,使得动态分配的顺序表适合存储大量数据或在多个作用域中共享数据。但是,堆内存的管理(分配和回收)速度相比栈要慢,并且需要手动管理,容易出错(如内存泄漏和碎片化问题)。
影响分析:
- 性能:栈内存的访问通常比堆内存快,因为栈是连续的内存块,由操作系统自动优化管理。在性能敏感的应用中,静态分配可以提供较优的性能。
- 灵活性:堆内存的使用提供了更高的灵活性,因为你可以根据需要动态地增加或减少数据存储空间。这在处理不确定数量的数据时非常有用。
- 生命周期:栈内存中的数据只在定义它的函数或作用域中有效,超出这个范围后就会被清除。而堆内存中的数据直到被显式删除之前都将持续存在,适用于需要跨多个函数或线程共享的数据。
因此,选择静态分配还是动态分配的顺序表,取决于具体的应用需求。如果应用场景中数据量固定且预先可知,静态分配是一个简单且高效的选择。对于需要灵活处理不同数据量的应用,动态分配则提供了必要的灵活性和效率。
2.3 线性表的链式存储方式——单链表
与顺序表不同,单链表中的元素不是存储在连续的内存位置上。而是每个元素包含其数据部分以及指向列表中下一个元素的指针,这种结构允许元素在内存中任意分布。由于这种独特的存储方式,单链表在插入和删除数据时可以更加灵活高效,无需像顺序表那样移动大量元素。
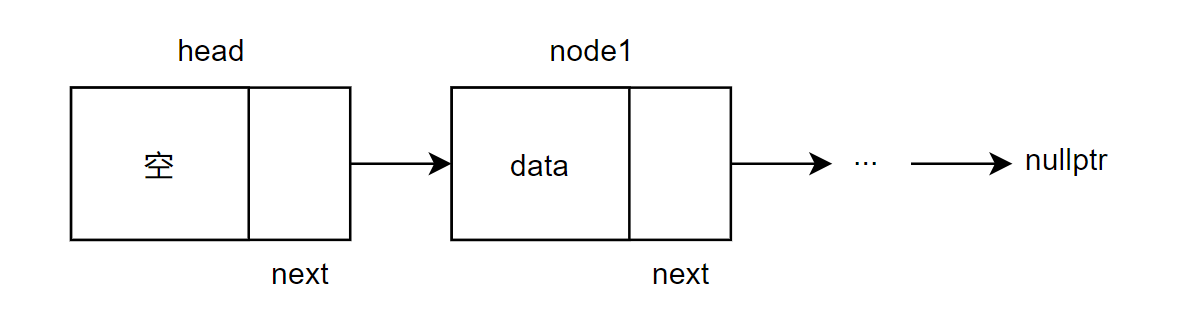
上图中的单链表是一个具有头结点的单链表。使用头结点后,对于单链表的插入和删除等操作,无需对第一个结点单独讨论,实际上,上图中 head->next 才表示单链表的第一个结点。需要注意的是头结点和头指针的区别:
- 头结点是一个实际的数据结点,它通常位于链表的最前端,并不包含实际的用戶数据(除非设计时有特别指定)。头结点主要是为了操作的方便而引入的,它的数据域通常不存储有效数据,而其指针域指向链表的第一个真实结点。
- 头指针是指向链表中第一个结点的指针。在链表中,头指针是必需的,因为它标记了链表的起始位置。在不使用头结点的链表中,头指针直接指向第一个含有实际数据的节点。在使用头结点的链表中,头指针指向头结点,而头结点的指针域指向第一个含有实际数据的节点。
2.3.1 单链表的实现
参考
- 零壹考研数据结构讲义



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· DeepSeek “源神”启动!「GitHub 热点速览」
· 我与微信审核的“相爱相杀”看个人小程序副业
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库
· 上周热点回顾(2.17-2.23)