线段树 算法分析
经过一年的调试......终于A了线段树的模板QAQ
线段树是什么:
线段树就是一棵完全二叉树,没啥好说的。线段树所存的不是一两个定值,而是一个\(\large{区间}\)。“线段树”顾名思义就是存了一个个线段(区间)的值。线段树最大的作用也就是省掉了批量修改的时间。譬如如果你要给\([114,514]\)区间中的每一个数\(+1\),一个一个地加就太慢了,我们就可以用到这个\(\tiny{\text{挨千刀}}\)的线段树了!首先我们先画一个线段树帮助理解!!
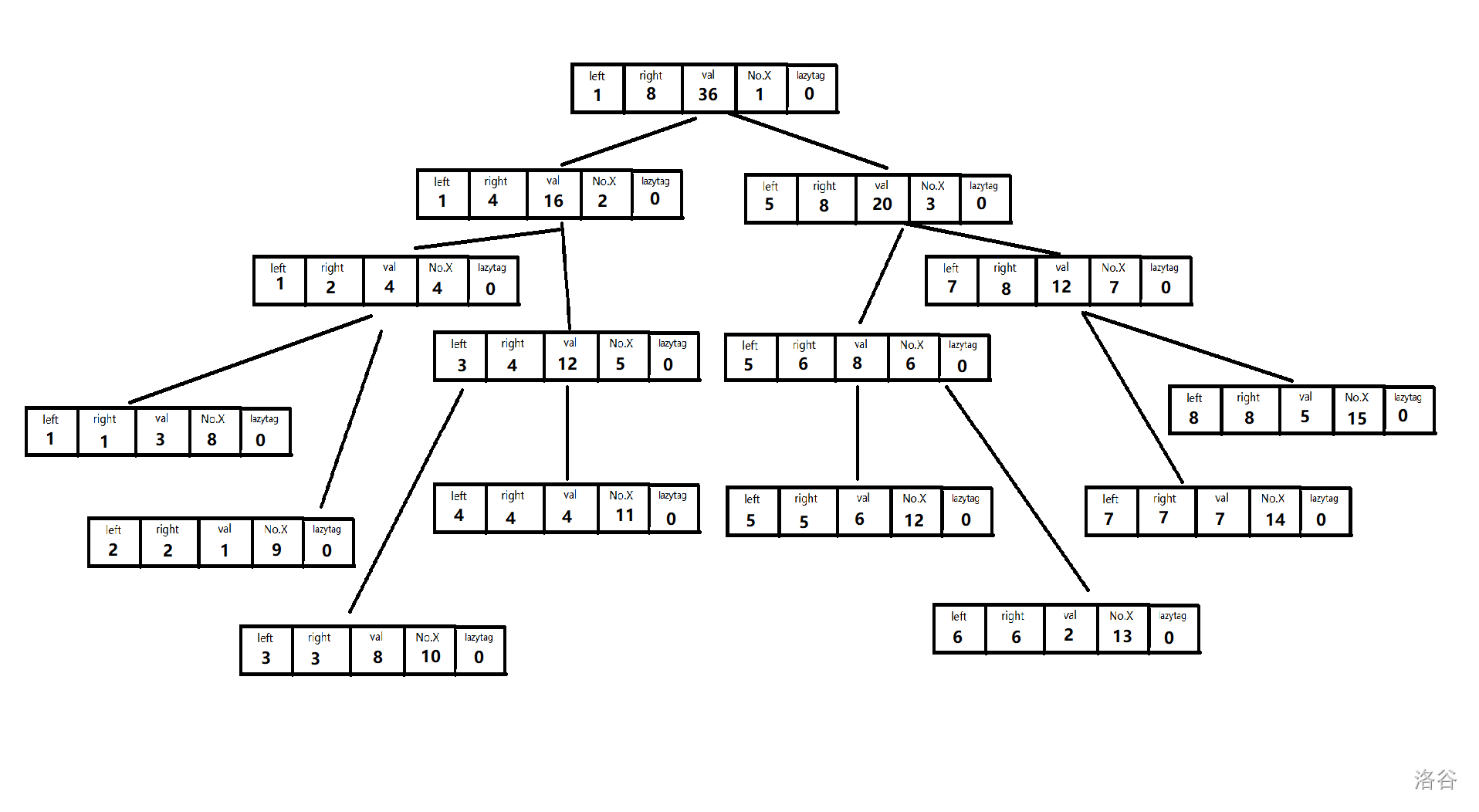
在图里,每一个节点都存储了\(4\)个数据:\(right\),\(left\),\(val\),\(lazytag\)。(No.X指的是该节点编号,仅方便看图)下面我们就来一一分析它们的作用。
1、\(left/right/val\)
这\(2\)个数组存的是线段树节点中最基本的元素:所存区间的边界。这很好理解,意思就是它管辖的就是原一维数组中下标为\(left\)~\(right\)的所有点的和(当然可以是其他的,比如最大值)
那么为啥要存区间呢?——因为修改的时候可以直接 \(O(1)\) 改变整个区间而不用再苦逼地一个个改变区间中的每一个值。而线段树的核心就在于如何改变整个核心——这样主角\(\text{懒标记}\)登场了!!!
2、lazytag懒标记
“懒标记”人如其名,
非常懒惰,但我们需要知道的是:懒人推动世界进步!。懒标记相当于是一个闸口,它可以自己选择是否将从线段树上方拿到的经费发放给下层的节点。譬如我要给区间\([l,r]\)中所有节点\(+1\),此时,懒惰且腐败的懒标记是不会让它下层的节点\(+1\)的,这是因为没有必要一个个地去改下层节点的值,只需要在它们的上司(\([l,r]\)区间的这个节点)那里记录一下就能够等价于将\([l,r]\)区间的所有节点\(+1\),而懒标记就记录了它的下层节点所需要改变的一个整体的量。所以说白了,懒标记所记录的就是一整个区间的\(\text{改变量}\)。
STEP.1
假设我们让区间\([2,6]\)内的所有数\(+8\)(注意这里指的是原始数组的区间\([2,6]\)),那么需要修改的线段树节点就是:\([2,2]\)&\([3,4]\)&\([5,6]\)。因为取出这\(3\)个节点就能改变最少的节点以刚好覆盖整个\([2,6]\)区间。(取$[1,8] || [1,4] || [5,8] || [1,2] \(都覆盖到了其他不需改变的节点,单独取\)[3,3][4,4][5,5][6,6]$又太慢了,不必要)。
STEP.2
那么我们现在就可以尝试直接改变\([2,2]\)&\([3,4]\)&\([5,6]\)的值,从而避免一个个地改动下方节点浪费时间。其实我们只需要把\(<\)有\(8\)元工资未给\(23456\)节点下发(它们没有\(+8\))\(>\)这个事实记录在懒标记上(\([2,2]\)&\([3,4]\)&\([5,6]\)的懒标记\(+8\))即可,需要分开的时候再去改变。
STEP.3
接下来我们需要计算\([2,2]\)&\([3,4]\)&\([5,6]\)的值:{改了几个点就加多少倍的值(区间\([l,r]\)改动的节点数就是 \(l-r+1\),那么这一点的值就必须要加上\((l-r+1)\times \Delta x\)(所加的值,比如上面的\(+8\))),因为这一点的值记录的是[l,r]区间的和,所以如果它的子节点每一个都有变动,那么这一段区间的和肯定会成倍地变动。}因此我们得出了在改变了懒标记后更新的公式:
STEP.4
最后我们就在回溯过程中更新它上层节点的值即可(\(val[father]=val[leftson]+val[rightson]\))
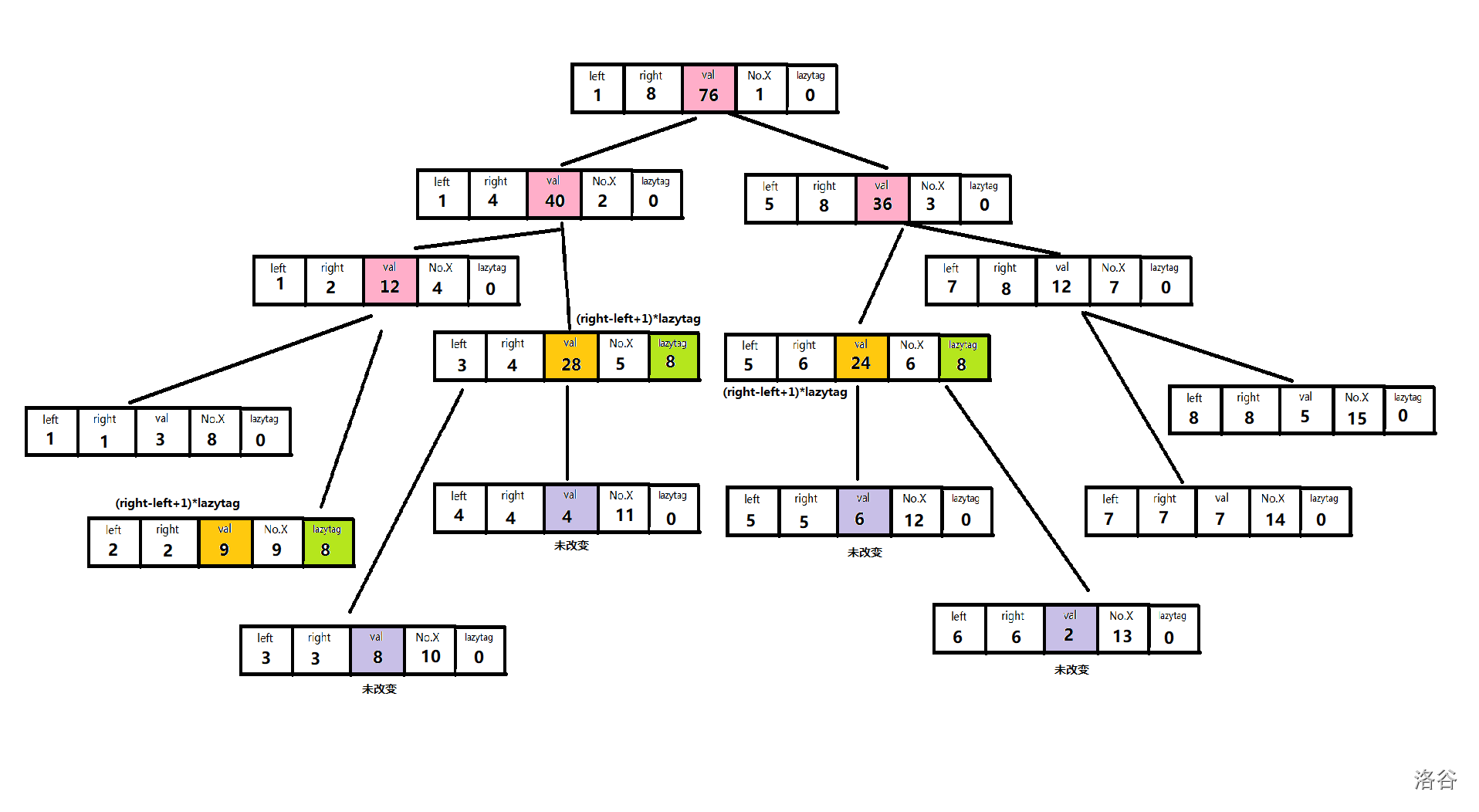
在上一个例子的基础上给区间[1,5]的数\(+3\)。
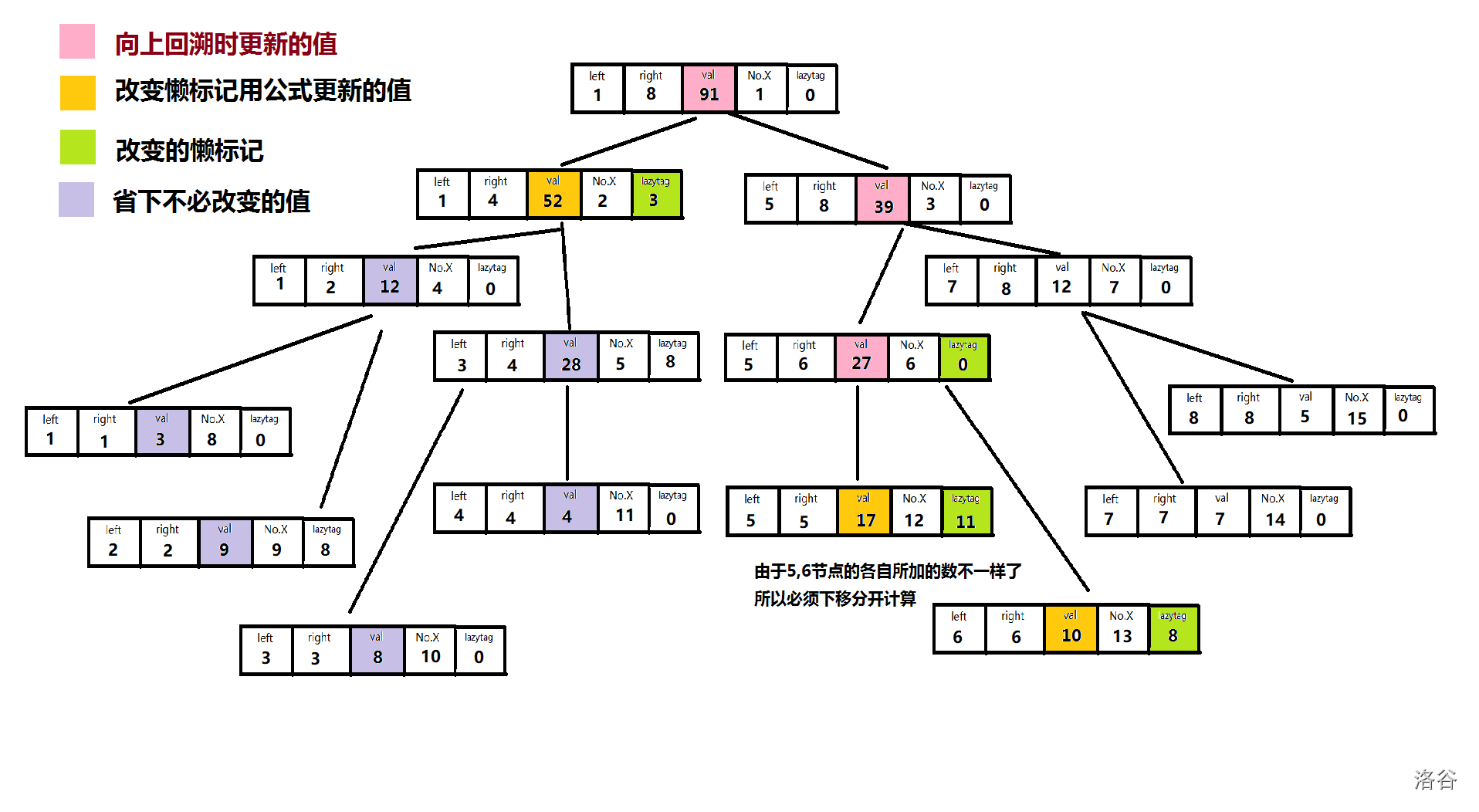
注意懒标记如果重叠在加法的线段树中可以直接相加,其他的可能不一定了。
2、计算答案
答案的计算就很善良了。经过上面的精神虐待以后,你肯定能够发现求值与加值有
异曲同工之妙。首先仍然是从根节点出发去寻找合适的区间即可,取到了合适的区间就直接ans+=val[dot]。唯一的问题就是你在寻找区间的时候,如果区间有分裂的情况 (比如你要找\([2,4]\),就必须要在\([1,4]\)区间分开寻找,因为我们不要\(1\)),此时就必须将懒标记下移,不然取不到准确的答案(如果不下移你就取多了\(1\)的值)。所以在向下寻找的过程中一定要记得下移懒标记哦!
#include<bits/stdc++.h>
#define Getmid(a,b) mid=(a+b)>>1
#define range(a,b,c) for(long long c=a;c<=b;++c)
#define L(a) a<<1
#define R(a) a<<1|1
#define N 4000005
using namespace std;
long long first[N];//初始的一维数组,没毛用。
long long dotNum,opeNum;//节点数(一位数组大小)和操作数。
long long dotleft[N],dotright[N];//dotleft/right存该节点的区间[l,r]。
long long val[N];//存该节点所存区间中各节点的和
long long tag[N];//懒标记,标记了某一点需要向下分发给每个子结点多少值。
long long Num,L,R;//3个有很多用处的用来标记加数、所查总区间的全局变量
long long ans;//在统计值的时候用到的暂时性的存储答案
//
void record(long long dot)//更新某一点的值(很多地方都要更新呢)
{
val[dot]=val[L(dot)]+val[R(dot)];//每一节点的值都为它2个子节点的值之和
}
//
void push_down(long long dot)//将节点懒标记下移(催它发工资)
{
val[L(dot)]+=(dotright[L(dot)]-dotleft[L(dot)]+1)*tag[dot];
val[R(dot)]+=(dotright[R(dot)]-dotleft[R(dot)]+1)*tag[dot];
//上两句即为将懒标记下移把值加给下移的目标节点(调配资金)
tag[L(dot)]+=tag[dot];//释放了dot点的懒标记分配给它的子节点
tag[R(dot)]+=tag[dot];//不是直接赋值因为有可能子节点已有懒标记(持续拖欠工资)
tag[dot]=0;//释放完后清零 (1个节点只有2个子节点(完全二叉树),所以释放完了可以直接清零)
}
//
void add(long long curl,long long curr,long long dot)//LR为目标区间,curl/r为现区间
{
if(curl>=L&&curr<=R)//如果节点的区间包含在大区间里
{
tag[dot]+=Num;//记录这一节点拖欠了它属下的工资数(每人)增加了
val[dot]+=(curr-curl+1)*Num;//记录这一点的总资产(子节点之和)
return;
}
else//如果节点的区间在大区间外或有一部分在大区间外
{
push_down(dot);//催促该节点向下发工资并继续查找它的手下一直到现区间包含在大区间中
long long Getmid(curl,curr);//找到现区间中点以尝试向哪一边继续查找
if(mid>=L)//以mid为中点分割,如果mid左边超出了大区间的边界即可直接抛弃
{
add(curl,mid,L(dot));//由于已经编好了号,所以易证每一个节点左儿子区间即为[l,mid]
}
if(mid+1<=R)//同理,如果mid右边越界就无需查找,判断它在界内才需要查找
//注意不能直接用else因为有可能它左右两边都在界内就都需要查找
{
add(mid+1,curr,R(dot));//同理,它右儿子的区间肯定是[mid+1,r]
}
record(dot);//分配完工资重新计算该点的总资产
}
}
//
void getsum(long long curl,long long curr,long long dot)
{
if(curl>=L&&curr<=R)
{
ans+=val[dot];//当一个节点的区间完全包含在整个区间中,则可以直接取到答案
return;
}
else
{
push_down(dot);
long long Getmid(curl,curr);
if(mid>=L)getsum(curl,mid,L(dot));//解释同上
if(mid+1<=R)getsum(mid+1,curr,R(dot));
record(dot);
}
}
//
long long buildtree(long long l,long long r,long long dot)
{
dotleft[dot]=l;//令所编号的节点区间左边界为l
dotright[dot]=r;//右边界为r,即记录下[l,r]
if(l==r)//如果一个区间只有1个点(l=r),证明二分完了,返回
{
val[dot]=first[l];//最后这点的值为它本身
return val[dot];//返回这点的值(效果见后)
}
long long Getmid(l,r);//如果不是叶子节点,找到区间中点准备二分
val[dot]=buildtree(l,mid,L(dot))+buildtree(mid+1,r,R(dot));
//每一点的值都是它儿子值的和(比如[l,r]的和即为[l,mid],[mid+1,r]这两个子区间的和)
return val[dot];//正因如此,返回这个子区间的和即可
}
//
int main()
{
scanf("%ld%ld",&dotNum,&opeNum);
for(long long i=1;i<=dotNum;++i)
{
cin>>first[i];
}
buildtree(1,dotNum,1);
for(long long i=1;i<=opeNum;++i)
{
int ope;//同时即可输入需要操作的区间[L,R] (下面一句)
cin>>ope>>L>>R;
if(ope==1)
{
cin>>Num;
add(1,dotNum/*[1,dotNum]的区间内查找*/,1/*根节点编号*/);
}
if(ope==2)
{
ans=0;
getsum(1,dotNum,1);//清空之前的答案并开始新一轮的统计
cout<<ans<<endl;
}
}
return 0;
}
填坑第 \(\huge{6}\) 站完成!
配套算法 ------> 树状数组


 浙公网安备 33010602011771号
浙公网安备 33010602011771号