Dijkstra & heap优化
1.Dijkstra算法简介
\(Dijkstra\)算法是目前OI中关于最短路问题的最实用方法。除了负权回路,\(Dijkstra\)算法对于所有的题目来说都是适用的。普通的\(Dijkstra\)算法复杂度与\(Bellman\)-\(Ford\)相当,优化后的\(Dijkstra\)算法可以媲美SPFA的速度,甚至比\(SPFA\)更快。由于目前的\(OI\)竞赛喜欢卡\(SPFA\)(即\(SPFA\)已死),所以\(SPFA\)的实用性远远不如\(Dijkstra\)(
更何况\(Dijkstra\)还是@Edmundino这位大佬最喜欢的算法)
2.普通的Dijkstra
算法介绍
我们首先讲的是未经优化的\(Dijkstra\),也就是\(Dijkstra\)的基本原理:
我们知道,\(Bellman\)-\(Ford\)和\(SPFA\)算法的核心是松弛操作,而\(Dijkstra\)的核心又双叒叕是松弛,\(Dijkstra\)与前两位大佬的区别仍然是遍历的过程。Dijkstra的遍历过程也很简单,首先以起点为 \(S\) 点,首先松弛以 \(S\) 为中心的点(即与 \(S\) 相连的点),然后将已经有值且未被查找的点中最小的一个点提出来(设它是 \(A\) 点)再以 \(A\) 点为中心松弛与 \(A\) 相连的点,然后再次选出松弛后未查找的所有点中值最小的点(点 \(B\) ),以 \(B\) 为中心进行松弛,并以此类推。(注:因为要判断一个点是否被查找,我们可以建一个\(bool\)数组判断每个点有冇被查找。例如一个\(jud\) 数组,\(jud_i=false\) 表示 \(i\) 未被查找,反之则已被查找,以下的 \(jud\) 数组即表示该含义("\(\text{judge}\)"),找最小值是就需要联立两个数组查找)
举个栗子
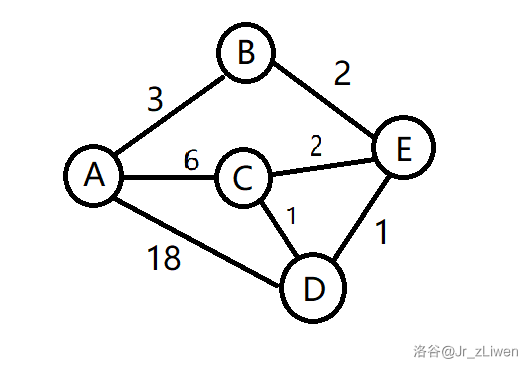
\(\tiny{\text{ps: 其实还是上次的图}}\)
我们
还是以 \(A\) 点为起点,首先我们对与A相连的\(BCD\)三点进行松弛操作,把\(BCD\)的值从\(∞\)改变成了对应边的值\((3,6,18)\)。那么很显然,此时:
注:\(jud_1\text{表示的是}jud_A,jud_2\text{表示的是}jud_B,\text{以此类推。}\)
现在,我们就可以选出满足( \(jud_X=0\) ) 的点中值最小的点(即点 \(B\) ) ,然后再对与点 \(B\) 相连的点 \(AE\) 分别进行松弛操作,\(A\) 不用更新,\(E\) 从\(∞\)变成了\(5\)。那么很显然,此时:
到了此时,我们就可以以此时满足( \(jud_X=0\) ) 的点中最小的点进行搜索,下一个搜的即为 \(E\)。(这里就可以体现出\(SPFA\)和\(Dijkstra\)之间的区别,\(SPFA\)此时应先搜索 \(C\),而现在我们先搜了 \(E\),而看到了结局的你应该知道E点可以改变\(D\)点的值,这就不用再向\(SPFA\)那样多搜一次\(D\)了),松弛与 \(E\) 相连的 \(BD\) 点松弛,把点 \(D\) 的值更新为\(6\)。(知道结局的你应该知道此时已经找到了最后的最优解,这就是\(Dijkstra\)与\(SPFA\)的区别,而优化\(Dijkstra\),就是在优化找最小值的时间)。很显然,现在:
接下来就是“以此类推”了,我就直接简写了:找 \(C\),没改变,找 \(D\),还是没改变(其实也没有简单多少QwQ)。那么最优解就找出来了:
那么,接下来我们就要将优化了!!!,因为优化其实真挺简单(
如果你手打了三天的堆模板),如果能用上\(STL\)的话那就——"有 · 手 · 就 · 行"。
Dijkstra 的 heap 优化
在理解\(Dijkstra\)的优化前,你可能需要堆的知识(其实是博主在写之前需要的),所以这里给出了堆排序和堆的详细讲解传送门:
那么如果你已经看完了上面那篇文章,或者你本来就熟知堆的算法,那么你肯定知道找最大值是可以从\(O(n)\)简化到\(O(log_2n)\)的。(即原本需要从头循环到尾去寻找最大值,那么此时我们可以轻轻松松地\(STL\)用在这里啦!!!(不就找个最大值嘛),不懂的赶快移步至堆的讲解,看完你就懂了!
那么最后的最后我们上代码!!!:
#include<bits/stdc++.h>
#define N 500001
using namespace std;
//
struct MAX
{
int dot,num;
bool operator<(const MAX &x)const
{
return x.num<num;
}
}res;
priority_queue<MAX> h;
//
struct node
{
int des,val;
}cnt;
vector<node>data[N];
bool used[N],jud;
int dis[N];
//
int main()
{
int dotNum,EdgeNum,origin;
cin>>dotNum>>EdgeNum>>origin;
for(int i=1;i<=EdgeNum;++i)
{
int a,b,c;cin>>a>>b>>c;
cnt.des=b;cnt.val=c;
data[a].push_back(cnt);
}
for(int i=1;i<=dotNum;++i)
{
dis[i]=0x7fffffff;
}dis[origin]=0;
res.dot=origin;res.num=0;
h.push(res);
used[origin]=1;
while(!h.empty())
{
res=h.top();h.pop();
int u=res.dot;
if(used[u]&&jud!=0)continue;
jud=1;
for(int i=0;i<data[u].size();++i)
{
int v=data[u][i].des;
int w=data[u][i].val;
if(dis[u]+w<dis[v])
{
dis[v]=dis[u]+w;
res.num=dis[v];res.dot=v;
h.push(res);
}
}
used[u]=1;
}
for(int i=1;i<=dotNum;++i)
{
cout<<dis[i]<<' ';
}
return 0;
}
填坑第\(\huge{5}\)站完成!!!

