剑指 Offer 47. 礼物的最大价值

 

 一个二维的动态规划的题目，之前见过类似的

 

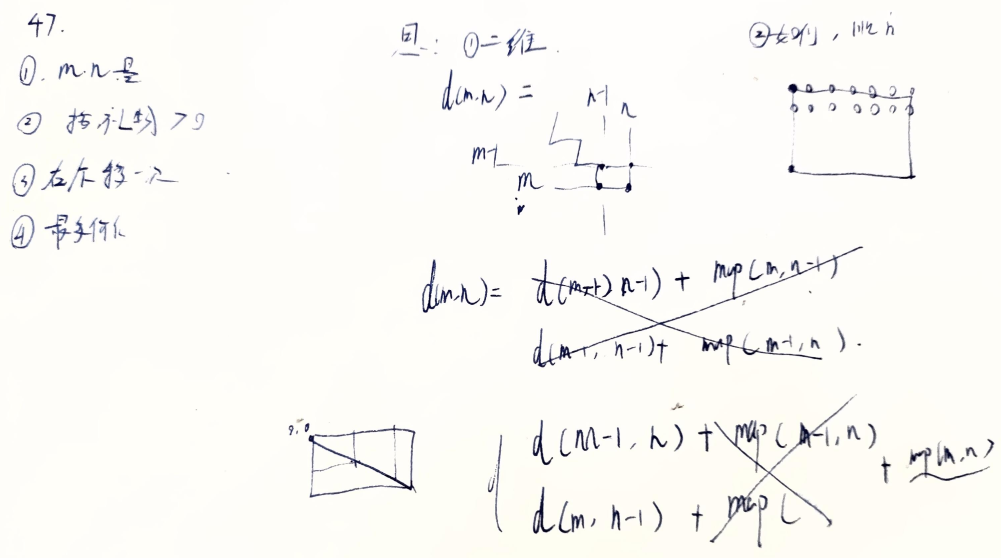
 递推方程很好写：

dp(m,n)=max(dp(m-1,n),dp(m,n-1)+map(m,n),边缘的则特殊处理

至于怎么写for循环，自然想到是两层for循环写完：

于是代码如下：

class Solution {
    public int maxValue(int[][] grid) {
        int m=grid.length;
        int n=grid[0].length;//grid>0
        int[][] dp=new int[m][n];//写错为int[][] dp=new dp[m][n];
        dp[0][0]=grid[0][0];
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(i==0&&j==0)
                {continue;}
                else if(i!=0&&j==0)
                {dp[i][j]=dp[i-1][j]+grid[i][j];}
                else if(i==0&&j!=0)
                {dp[i][j]=dp[i][j-1]+grid[i][j];}
                else
                {
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])+grid[i][j];
                }
            }
        }
        return dp[m-1][n-1];

    }
}

 

写错为int[][] dp=new dp[m][n];

注意new数组的时候老写错：

另外返回值是 dp[m-1][n-1]，注意这是length，要减去1的

 

优化的第一点在于，由于map(m,n)用完一次就不需要用了，可以直接用原始矩阵放置

 

 

 

优化第二点

当 gridgrid 矩阵很大时， i = 0i=0 或 j = 0j=0 的情况仅占极少数，相当循环每轮都冗余了一次判断。因此，可先初始化矩阵第一行和第一列，再开始遍历递推。

class Solution {
    public int maxValue(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        for(int j = 1; j < n; j++) // 初始化第一行
            grid[0][j] += grid[0][j - 1];
        for(int i = 1; i < m; i++) // 初始化第一列
            grid[i][0] += grid[i - 1][0];
        for(int i = 1; i < m; i++)
            for(int j = 1; j < n; j++) 
                grid[i][j] += Math.max(grid[i][j - 1], grid[i - 1][j]);
        return grid[m - 1][n - 1];
    }
}

比较tricky了可谓是