01-抽象数据类型
一.作业题目
实验题目
试仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 (有理数是其分子、分母均为整数且分母不为零的分数)。
有理数基本运算如下所示:
- 1.构造有理数T,元素e1,e2分别被赋以分子、分母值
- 2.销毁有理数T
- 3.用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
- 4.将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
- 5.有理数T1,T2相加
- 6.有理数T1,T2相减
- 7.有理数T1,T2相乘
- 8.有理数T1,T2相除
补充:加减乘除运算结果我存入的是有理数T1
实验要求:
- 抽象数据类型名为Rational。
- 有理数分母不能为负数或者0,类似输入请提示重输入。
- 数据对象和数据运算的表示与数据操作的实现分离。表示用头文件完成,实现用CPP文件完成。Main.cpp文件实现数据输入输出。
- 数据输入输出格式参考如下:
输入:
1 3 //T1的分子、分母
1 2 //T2的分子、分母
** 输出:**
5 6 //两个有理数相加
-1 6 //两个有理数相减
1 6 //两个有理数相乘
2 3 //两个有理数相除 - 程序应对异常输入或者出错必要处理和提示,分子分母要约分。
二、博客作业要求:
1.作业内容
用ADT的抽象数据模型描述你的有理数数据类型。
ADT Rational
{ 数据对象:
D={e1,e2|e1,e2均为实数}
数据关系:
R={<e1,e2>|e1是有理数的分子部分,e2是有理数的分母部分}
基本运算:
InitRational(rational,e1,e2):构造有理数T,其分子和分母分别赋以参数v1,v2的值
DestroyRational(rational):销毁有理数T
Get(rational,choice):提取分子或分母
Yuefen(rational):对分子分母进行约分
Put(rational, choice):修改分子或分母
Add(rational,rationalnew):俩个有理数相加
Minus(rational,rationalnew):俩个有理数相减
Multiply(rational,rationalnew):俩个有理数相乘
Divided(rational,rationalnew):俩个有理数相除
}ADT Rational
2.数据结构、函数说明
截图展示你的头文件。头文件代码务必加入注释。


3.代码实现说明
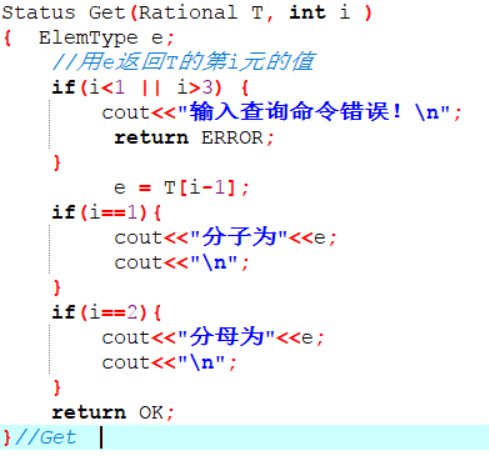
截图展示每个函数代码。简要说明做法。
- 构造有理数:正确输入e1,e2,给T申请空间,将e1,e2的值存在T数组中,T[0]表示分子,T[1]表示分母
- 销毁有理数:释放T的空间
- 查询分子或分母的值:通过i的输入,输出对应数组的值,即输出分子分母的值
- 修改分子或分母的值:通过i的输入,修改对应数组的值,即修改分子分母的值
- 有理数的加法运算:再构造一个新的有理数,对俩个有理数进行通分相加并约分化简
- 有理数的减法运算:再构造一个新的有理数,对俩个有理数进行通分相减并约分化简
- 有理数的乘法运算:再构造一个新的有理数,对俩个有理数进行相乘并约分化简
- 有理数的除法运算:再构造一个新的有理数,对俩个有理数进行相除并约分化简
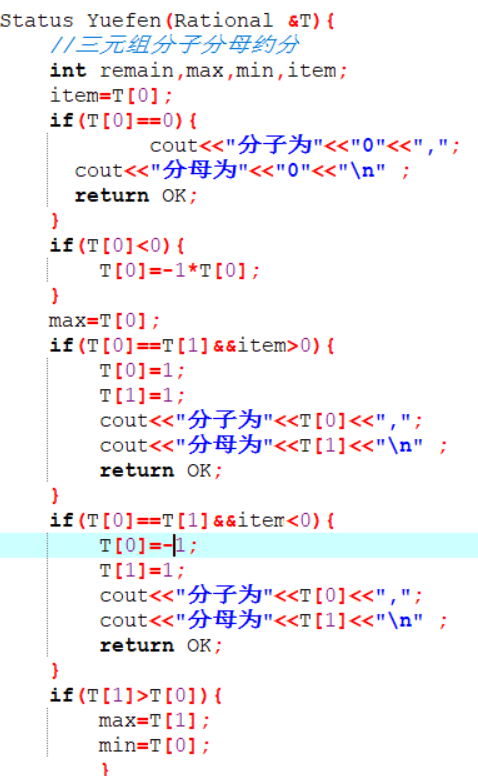
- 约分:利用辗转相除法找到最小公倍数,分子分母同除最小公倍数,注意分子小于等于0的情况






5.结果展示
每种测试数据一个截图结果。测试数据越多,此项得分越高。务必考虑临界数据,如分母为负数或0情况等等。
构造有理数
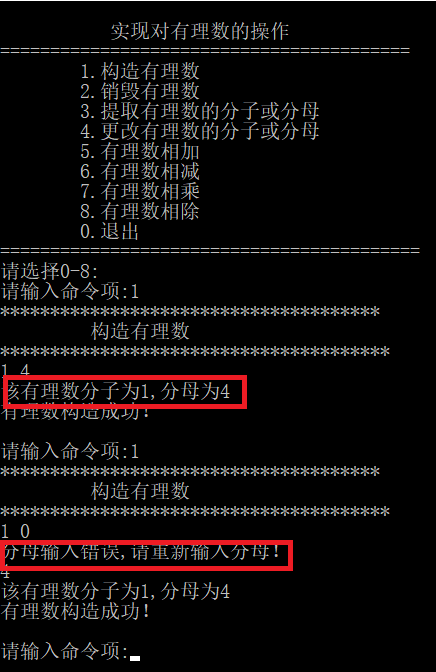
销毁有理数

正确查询输出查询结果,错误查询无结果
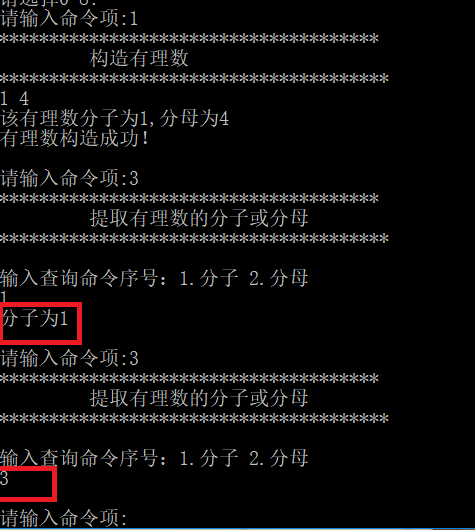
修改分子或分母
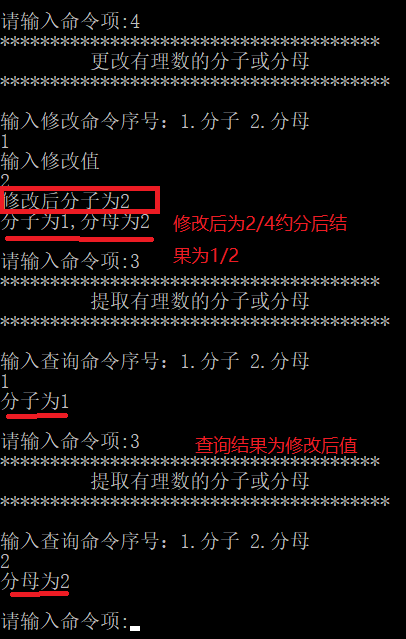
运算操作有理数分子均大于0
有理数加减


有理数乘除

运算操作有理数分子小于0


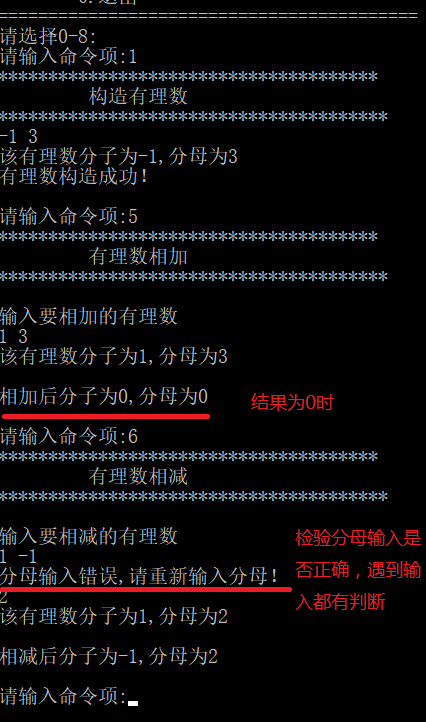
补充:运行过程中发现一些没有处理好的,后面代码还可以有小改动,像结束操作时销毁俩个有理数,还有判断分母输入是否正确时,代码展示部分只能判断一次,再输入时分母即使是0或者负数依然顺利输入不能提示错误,可以改成while循环,还有输入时一些提示语句可以再完善一点
退出操作
6.总结
谈谈你对数据结构及抽象数据类型的理解。
(1)数据结构包括俩个部分,一是数据,二是数据间的关系。数据结构包括数据元素间的逻辑关系,数据元素和关系在计算机中的储存方式,还有就是数据运算这几个方面。
(2)逻辑结构包括集合,线性,树,图;存储结构主要有顺序的和链式的;数据运算最常用的有检索,插入,删除,排序等
(3)抽象数据类型适合不大容易表示出来的数据,比如像这次的有理数分子分母,还有课本上的复数。可以通过数组或者结构体数组来将组成数据的部分分装储存并进行操作




