[离散时间信号处理学习笔记] 8. z逆变换

z逆变换的计算为下面的复数闭合曲线积分：

$x[n] = \displaystyle{\frac{1}{2\pi j}}\oint_{C}X(z)z^{n-1}dz$

式中$C$表示的是收敛域内的一条闭合曲线。该积分表达式可以利用复数变量理论下的柯西积分定理推导得到。不过本门课程用不上这条式子，因为在离散LTI系统分析中所遇到的典型序列和z变换，有如下更简单的z逆变换求解办法。

 

观察法（查表）

下面是一个常见序列的z变换表格，通过查表可以由z变换所得的函数反过来求得原序列

Sequence

Transform

Region of convergence

1. $\delta[n]$	$1$	for all $z$
2. $u[n]$	$\frac{1}{1-z^{-1}}$	$|z|>1$
3. $-u[-n-1]$	$\frac{1}{1-z^{-1}}$	$|z|<1$
4. $\delta[n-m]$	$z^{-m}$	$z\neq\left\{\begin{matrix}0 &,& m>0 \\ \infty &,&m<0\end{matrix}\right.$
5. $a^nu[n]$	$\frac{1}{1-az^{-1}}$	$|z|>a$
6. $-a^nu[-n-1]$	$\frac{1}{1-az^{-1}}$	$|z|<a$
7. $na^nu[n]$	$\frac{az^{-1}}{(1-az^{-1})^2}$	$|z|>a$
8. $-na^nu[-n-1]$	$\frac{az^{-1}}{(1-az^{-1})^2}$	$|z|<a$
9. $cos(\omega_0n)u[n]$	$\frac{1-cos(\omega_0)z^{-1}}{1-2cos(\omega_0)z^{-1}+z^{-2}}$	$|z|>1$
10. $sin(\omega_0n)u[n]$	$\frac{sin(\omega_0)z^{-1}}{1-2cos(\omega_0)z^{-1}+z^{-2}}$	$|z|>1$
11. $r^ncos(\omega_0n)u[n]$	$\frac{1-rcos(\omega_0)z^{-1}}{1-2rcos(\omega_0)z^{-1}+r^2z^{-2}}$	$|z|>r$
12. $r^nsin(\omega_0n)u[n]$	$\frac{rsin(\omega_0)z^{-1}}{1-2rcos(\omega_0)z^{-1}+r^2z^{-2}}$	$|z|>r$
13. $\left\{\begin{matrix}a^n ,& 0\leqslant n\leqslant N-1\\0 ,& else\end{matrix}\right .$	$\frac{1-a^Nz^{-N}}{1-az^{-1}}$	$|z|>0$

 

 

部分分式展开法

不过也经常出现输入序列为组合序列的情况，这种序列的z变换就是它的组成序列的z变换的线性组合。

如果某个输入序列是这些典型序列的线性组合，那么这个输入序列的z变换就能表示成各个典型序列的z变换之和

$x_1[n]+x_2[n]+x_3[n]+\cdot\cdot\cdot\stackrel{\mathcal{Z}}{\longleftrightarrow}X_1(z)+X_2(z)+X_3(z)+\cdot\cdot\cdot$

 

分式展开法

观察上面的表格可以发现大多数典型序列的z变换都是分数形式，因此这些z变换的组合可以假设为

$\displaystyle{X(z) = \frac{b_0}{a_0}\frac{\prod_{k=1}^{M}(1-c_kz^{-1})}{\prod_{k=1}^{N}(1-d_kz^{-1})}}$

其中$c_k$是$X(z)$的非零值零点，$d_k$是$X(z)$的非零值极点。分母是各个典型序列的分母的乘积，把各个典型序列的z变换（分数）相加就能得到上面的式子。

 

$M<N$

若$M<N$，并且极点都是一阶（即没有相同的极点，即没有相同的$d_k$）的，那么$X(z)$就能表示为

$X(z) = \displaystyle{\sum_{k=1}^{N}\frac{A_k}{1-d_kz^{-1}}}$

此时，等式两边乘以$(1-d_kz^{-1})$，并取$z$等于其中的某个极点$z=d_k$，可以消去等式右边除了$A_k$之外所有的项

$(1-d_kz^{-1})X(z)|_{z=d_k} = A_k$

按照这种计算方式可以得到所有的$A_k$，然后通过查表即可得到各个和式所对应的序列。

 

$M\geqslant N$

若$M\geqslant N$则可以用长除法，分子除以分母以使得分式的$M<N$，然后就可以按照上述方法继续求解

$X(z) = \displaystyle{ \sum_{r=0}^{M-N}B_rz^{-r} +\sum_{k=1}^{N}\frac{A_k}{1-d_kz^{-1}}}$

 

重复极点

如果$X(z)$有多重极点在$z=d_i$，阶数为$s$（在该极点上有$s$个重复极点）,而且$M\geqslant N$，那么有

$X(z) = \displaystyle{ \sum_{r=0}^{M-N}B_rz^{-r} +\sum_{k=1,k\neq i}^{N}\frac{A_k}{1-d_kz^{-1}}+\sum_{m=1}^s\frac{C_m}{(1-d_iz^{-1})^m}}$

其中$C_m$由如下式求得

$\displaystyle{C_m = \frac{1}{(s-m)!(-d_i)^{s-m}}}\left\{ \frac{d^{s-m}}{d\omega^{s-m}}[(1-d_i\omega)^sX(\omega^{-1})]\right \}_{\omega=d_i^{-1}}$

 

例子

考虑有一序列$x[n]$，其z变换为

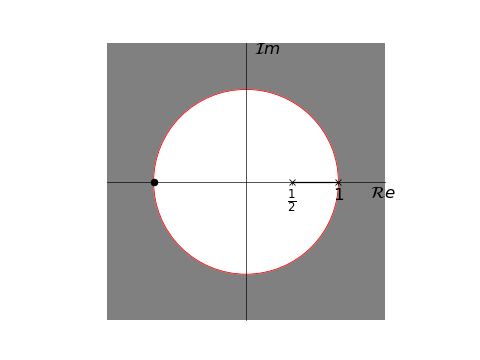
$X(z) = \frac{1+2z^{-1}+z^{-2}}{1-\frac{3}{2}z^{-1}+\frac{1}{2}z^{-2}}=\frac{(1+z^{-1})^2}{\left(1-\frac{1}{2}z^{-1} \right )(1-z^{-1})}\qquad |z|>1$

右下图为$X(z)$的零-极点图

• 根据收敛域可知序列$x[n]$为一个右边序列
• 观察$X(z)$可发现其两个极点都是一阶的
• 因为$X(z)$的分子分母都是二次的，即$M=N=2$

因此$X(z)$可表示为

$X(z) = B_0+\frac{A_1}{1-\frac{1}{2}z^{-1}}+\frac{A_2}{1-z^{-1}}$

其中常数$B_0$能用长除法求得

$\begin{align*}
& &2\\
&{\frac{1}{2}z^{-2}-\frac{3}{2}z^{-1}+1} &\overline{\left )z^{-2}+2z^{-1}+1\right.}\\
& &\underline{z^{-2}-3z^{-1}+2}\\
& &5z^{-1}-1
\end{align*}$

余项为一次项，即$M<N$，因此$X(z)$可以写成

$X(z) = 2+\frac{-1+5z^{-1}}{\left(1-\frac{1}{2}z^{-1} \right )(1-z^{-1})}$

接下来求系数$A_1$以及$A_2$

$\begin{align*}
A_1 &= \left[\left(2+\frac{-1+5z^{-1}}{\left(1-\frac{1}{2}z^{-1} \right )(1-z^{-1})} \right )\left(1-\frac{1}{2}z^{-1} \right ) \right ]_{z=1/2} = -9\\
A_2 &= \left[\left(2+\frac{-1+5z^{-1}}{\left(1-\frac{1}{2}z^{-1} \right )(1-z^{-1})} \right )\left(1-z^{-1} \right ) \right ]_{z=1} = 8
\end{align*}$

因此

$X(z) = 2-\frac{9}{1-\frac{1}{2}z^{-1}}+\frac{8}{1-z^{-1}}$

查表可得

$x[n] = 2\delta[n]-9\left( \frac{1}{2} \right)^nu[n]+8u[n]$

 

 

幂级数展开法

如果$X(z)$由如下幂级数的形式给出时

$X(z) = \cdot\cdot\cdot+x[-2]z^{2}+x[-1]z^{1}+x[0]+x[1]z^{-1}+x[2]z^{-2}$

如果该多项式长度有限，我们就能得到该序列的所有的值。

如果该多项式无限长，我们可以观察该多项式是否能表示成如下形式

$X(z) = \displaystyle{ \sum_{n=-\infty}^{\infty}f(n)z^{-n} }$

如果能转换成这种形式，就可以得到序列$x[n] = f(n)$