Atcoder AGC001 解题报告
\(A.\ BBQ\ Easy\)
简要题意：
将\(2N\)个数字分成两个一组，每一组的价值是较小的数字，求总的价值最大的分组方案。
题目解法：
题目相当于将数字分成两组\(A\)和\(B\)，使得分别排序后，都是\(A_i \leq B_i\)，并且最大化\(\sum A_i\)。
将原数组排序，设为\(\{S_i\}\)，那么有\(S_1 \in A\)。
我们的目标是最大化\(\sum A_i\)，等价于最小化\(\sum B_i\)。
那我们就可以用\(S_1\)将\(S_2\)拼掉，也就是将\(S_2\)放在\(B\)中，这一定是最优的。
此时问题规模就缩小了，就可以继续做了。
所以说，答案就是排序之后奇数位的数字和。
\(B. \ Mysterious\ Light\)
简要题意：
有一个边长是\(N\)的正三边形，从距离一个顶点\(X(X<N)\)处，平行于一条直线射入三角形。
与特殊的光线不同，这一束光可以被自己的轨迹反射（当然，也可以被三角形反射）。
可以证明，这束光最终一定会回到出发点，求出这束光回到出发点之前经过的路径长度。
题目解法：
这道题，个人感觉就是肉眼观察题，如图：
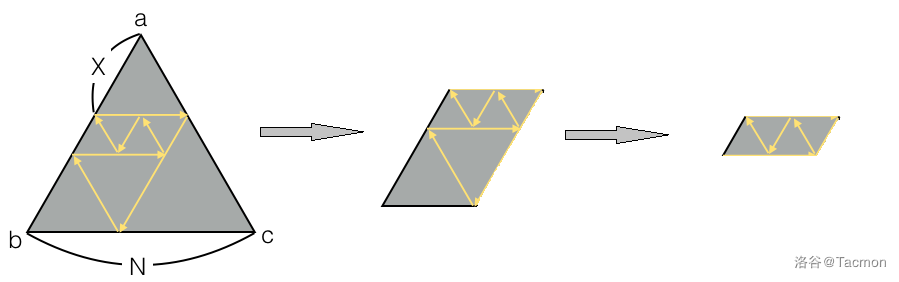
（忘了在图中标出长度和点了。。。将就一下吧。）
通过图，我们发现，如果用第一条和第二条分割三角形，就可以得到一个平行四边形。
而且光束一定是从其中一个大小是 \(\frac{2 \pi}{3}\)的角射入，最终只有两种情况：
- 光束正好到达出发点（另一个 \(\frac{2 \pi}{3}\) 角），此时一定有：长边长度\(a\)是短边长度\(b\)的倍数。
- 否则，就可以转化成一个子问题：长边是\(y\)，短边是\(x \mod y\)。
那么我们就可以用类似欧几里德算法的递归方式求解了。
\(C. \ Shorten\ Diameter\)
简要题意：
给定一个无根树，可以进行若干次如下操作，使得这棵树直径长度不超过\(K\)。
选择一个叶子，将其及其邻边删除。
求最少进行多少次操作，能够达成目标。
题目解法：
最开始想的是重心一定不会删，于是以重心为根树形DP。。。
事实证明我\(naive\)了，一是重心可能删，二是我的\(DP\)应该是\(N^3\)或\(N^2\log{N}\)的。
好吧，最终还是参考了其他人的解法：
题目是最小化删点个树，也就是最大化留下的点的个树。
于是分\(K\)是奇数还是偶数讨论：
(1) \(K \equiv 0 (\mod 2)\)
此时，我们一定能找到一个点，剩下的点中距离这个点最远的点，距离不超过\(\frac{k}{2}\)。
(1) \(K \equiv 1 (\mod 2)\)
此时，我们一定能找到一条边，剩下的点中距离这条边最远的点，距离不超过 \(\frac{k-1}{2}\) 。
这两种情况我们都能枚举枚举点或边，再\(O(N)\)计算，总的就是\(O(N^2)\)。
\(D. \ Arrays\ and\ Palindrome\)
简要题意：
原本有两个数组\(\{ A \}\)和\(\{ B \}\)，满足以下性质：
- \(\sum A = N\), \(\sum B = N\), \(Ai, Bi \in N_{+}\)
- 只有每一个位置都相同的长度为\(N\)的数组，才满足这两个性质：
(1)：将这数组分段：开头\(A_1\)个数，再\(A_2\)个数，再\(A_3\)个数\(\dots\)以此类推，使得每一段都是回文的。
(2)：将这数组分段：开头\(B_1\)个数，再\(B_2\)个数，再\(B_3\)个数\(\dots\)以此类推，使得每一段都是回文的。
但是现在，这两个数组都丢了，只知道\(N\)、\(M\) (\(\{ A \}\)的长度) 以及将\(\{ A \}\)打乱之后的数组\(\{ C \}\)。
请构造一组原来的\(\{A \}\)和\(\{ B \}\)。
题目解法：
我们思考一下那个回文的限制：
如果我们将每一组的回文对应位置（也就是一定相等的位置）连一条边，那么这\(N\)个点是在同一个联通块里的。
我们思考一下这些边怎么来的,如果存在一个长度为\(len\)的区间回文限制，那么我们就能连\(\left\lfloor\frac{len}{2}\right\rfloor\)条边。
众所周知，\(N\)个点要联通，最少要\(N-1\)条边。
那么就可以得到，如果\(\{ C \}\)中有大于两个奇数，就无解了，这是因为每一个奇数段，都会空出一个点，如果有三个空出来的就会少两条边，连树都不能构成了。
满足这个条件，我们就可以构造\(\{ B \}\)了，就是按照将每一段的中心错开，将每一条边错开的原则。
具体的说：将\(\{C\}\)的奇数放在两端，就是\(\{ A \}\)了，再将\(A_1-=1\)，\(A_M+=1\)，就是\(\{ B \}\)了，代码真简单。
\(E. \ BBQ\ Hard\)
简要题意：
给出\(N\)个二元组\((A_i,B_i)\)，求下面式子的值：
题目解法：
我们回想一下\(x+y \choose x\)的组合意义：从\((0,0)\)到\((x,y)\)的路径条数。
那么我们可以拓展到\((x_1-x_0)+(y_1-y_0) \choose (x_1-x_0)\)就是从\((x_0,y_0)\)到\((x_1,y_1)\)的路径条数。
可以发现，从\((-x_0,-y_0)\)到\((x_1,y_1)\)的路径条数就是和题目一样的形式了。
那么我们可以将题目先变形：
现在就只要考虑求出任意两个数之间的贡献了，这个经过上面的转化很好做：
我们考虑一个\(x \in [-2000,2000], y \in [-2000,2000]\)的直角坐标系，
最开始，在所有的\((-A_i,-B_i)\)上加一个一，之后DP，用组合数的递推就好了。
\(F. \ Wide\ Swap\)
简要题意：
给定一个排列，每次操作可以交换差值为1并且距离大于\(K\)的两个数。
求出能构造出来的字典序最小的排列。
题目解法：
因为距离大于\(K\)这个限制很恶心，考虑在这个排列的逆（也就是位置排列）上操作：
那么每次就是选相邻的而且差值大于\(K\)的两个数交换，而且因为是逆，所以我们现在是要最大化字典序了。
能够发现，如果两个数差值小于等于\(K\)，那这两个数的相对位置一定不会改变。
就相当于是前面的数向后面的数连一条边，之后的拓扑序就是一个合法的排列，也可以最大化字典序了。
但是这样有\(O(N^2)\)条边，不可行，考虑利用传递性去掉一些边，例如\((x,y)\)、\((y,z)\)和\((x,z)\)，其中\((x,z)\)没用。
这样的话，我们就从后往前向后面的点连边，但是只需要连两条：这个数\(\pm K\)的范围，正负各连一条到满足要求的最近的点（因为其他的合法的点一定会连到这两个点）。
这个连边操作可以用线段树简单实现，之后就是跑一遍拓扑序的事儿了。
