经验风险VS风险函数

二者基本概念

经验风险( Empirical Risk) : 损失函数度量了单个样本的预测结果，要想衡量整个训练集的预测值与真实值的差异,将整个训练集所有记录均进行一次预测, 求取损失函数,将所有值累加,即为经验风险。

就是已知的数据按照现有的模型，测试预测值和真实值偏离的程度叫经验风险。

经验风险越小说明模型f(x)对训练集的拟合程度越好。

 

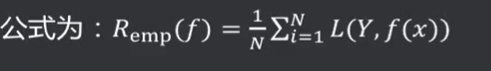
 风险函数( Risk Function) :又称期望损失、期望风险。所有数据集(包括训练集和预测集,遵循联合分布P(X,Y) )的损失函数的期望值。

 

 

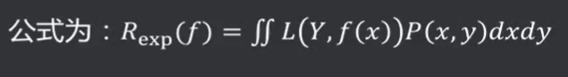
二者差异

 

 

 

经验风险的问题

在样本较小时，仅关注经验风险，很容易就导致过拟合。

过拟合：对当前的样本数据效果非常好，损失函数什么的非常低，但是如果碰到新的数据集，预测效果很差。

 

 经验风险低，模型就一定好吗？

 

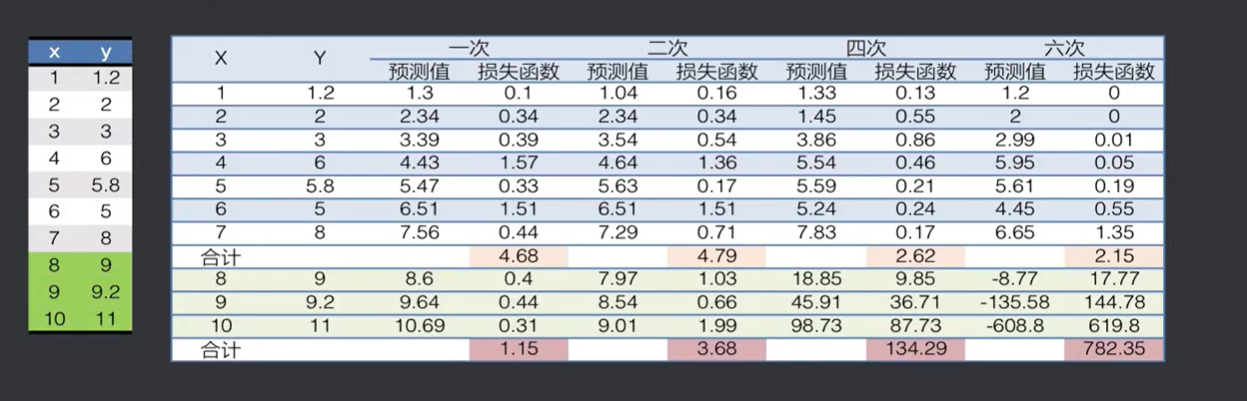
 左边是数据全集，上面是训练集，下面是预测集，可以看到训练集第六次是效果最好的，而预测集第一次效果最好。

 

结构风险

结构风险( Structural Risk) : 在经验风险的基础上，增加一个正则化项( Regularizer )或者叫做惩罚项( Penalty Term) , 公式为: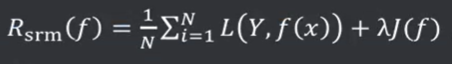

 

 

，其中λ为一个大于0的系数，J(f) 表示模型f(x)的复杂度。

 

 

正则化项

 

 

 

   六次模型的惩罚项特别大，他的结构化风险会远远大于一次模型，而经验风险是一次模型的更大，结构风险却小很多，

 

范数

规则化函数λJ(f)有多种选择,一般地,它是模型复杂度的单调递增函数,模型越复杂，该函数的值就越大，惩罚力度相应的越大。常用模型的参数向量的范数。常用的有零范数、一范数、二范数、迹范数、Frobenius范数和核范数等等。

 

 

 

L0范数:非0的元素的个数。使用L0范数,期望参数大部分为0 ,即让参数是稀疏的。

L1范数:各个元素的绝对值之和,使用L1范数,会使参数稀疏。L1也被称为稀疏规则算子。

L2范数:各元素的平方和求平方根，使得每个元素都很小,但不会等于0 ,而是接近0。

 

 

 

总结：

很多时候我们都想通过模型的期望风险值来判断模型好坏，但是期望风险值要拿到全集的数据除了训练集之外预测集也要拿到，现实中，一般现实中不会出现这种情况，期望风险只是一个理想的情况，很多时候一些数据是拿不到的，可以使用经验风险，它在提供的训练集上效果最好，拟合效果最好，但是经验风险有它的问题，容易产生过拟合，在训练集上还好，到了预测集就一塌糊涂，怎么去避免这个问题呢，就引入了一个结构风险，如果只靠经验风险来看拟合程度的话只会使其变得复杂，引入结构风险就是为了增加一个惩罚项，如果模型过于复杂，就会抛弃掉，让你的惩罚项变的很大，就不会被选择上，起到了平衡作用。  结构风险=经验风险+惩罚项，经验风险保证的是你在我的训练集上拟合效果不错，惩罚项是你的拟合效果不错，不要基于过于复杂的模型，结构风险在选择模型的时候考虑的因素：1.在训练集表现不错，2.模型不要太复杂。

 

太复杂就不可靠。