Crypto-GUET梦极光杯-线下赛WP
Crypto-GUET梦极光杯-线下赛WP
Simple Cipher
题目描述:
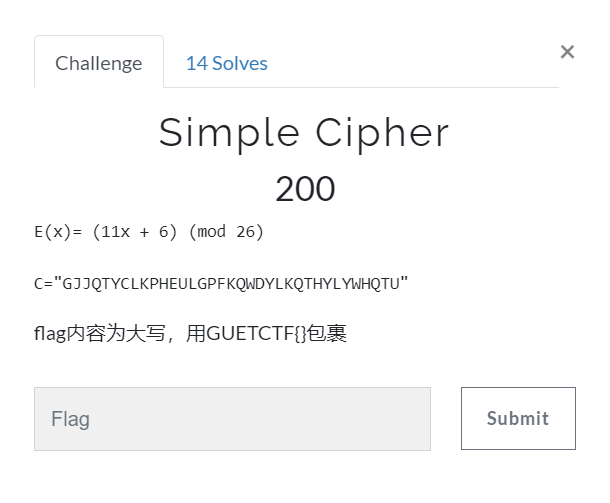
一眼就是仿射密码噻~洒洒水了
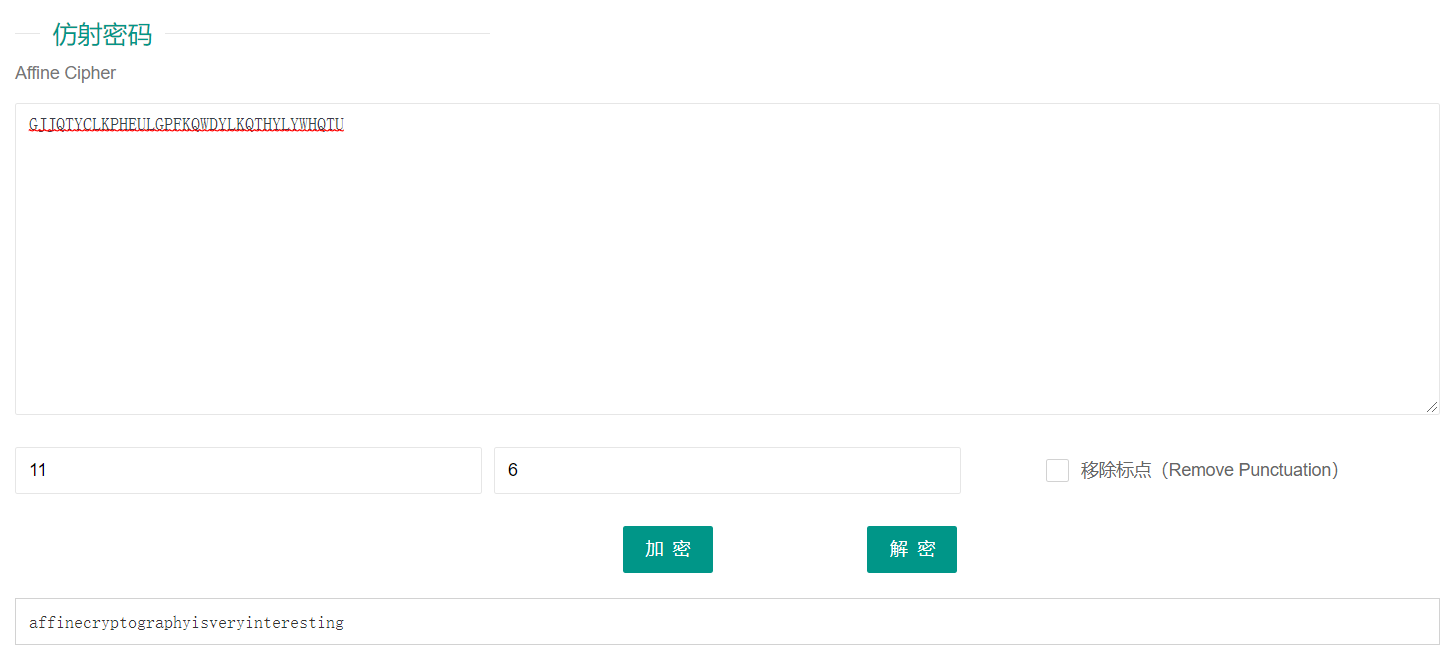
FLAG:GUETCTF{AFFINECRYPTOGRAPHYISVERYINTERESTING}
rsaRecov
题目描述:
下载解压打开附件后得到:
n=0x9f29e3566a1b337a700ca6b7e89f6f1acf8ee440c73d2efdf4aa0c4688b1c595c45889c186e64bb456fb43992c2b10e0caf58008afa99d824f57b6945d13e20f10a521f228f2f5b248014792df94249787f250b2b7379f470986c53bcf4b12fe26b91bbb2f07c210ed6119f6c24d9e53b69107908c3c29f4c99ee5cb6d35953f5902a94209e5a71a2db8307b239881cfba8894c6291de5949b1e717b33752820c9e5151f77d1bd7ba352c318f1ad305b1965d025affe39a8445807146034217aa54ad9b58a6f283af887284abe43b99dca468ffec00ab82863eca861bc6e5662268fe87ab4c69bb345341bf82cce2926cda811441db474220450988219f9b9ad
p=0xc0e32ed2f316de2a56d1f281aa015f0ec18009f6cf059abfe2193eab865203714d420ef58ff167608f00af025720abca4b83a09d7bbd5f9d16effd8b44718438cb7f32098a6dc4603c29d24888ef99be8e8d14be482f5f603be3ebf676250545682d05b1f62c569e7051d6ed63bd4e452b3fd787000000000000000000000000
e=65537
c=0x93b38eff708ee7bd46bbda06a7c648e34d40f1f54a14f02f49dd5e7e8cd659c7f4f1dcea919c9c7b8cbb710b9af8192f60cfca0e51ae50834eec2a912004f2a772c80bbed96ad9524b4b027474ae7880e0d65400c7155da81707b6bc0f61d5405eea79ccaf77af71bb974e82b8e7cc83d594f38ce47e93afc5fca1a340dbd4acaaf091dac93d1069f544a1d734893f2dd7856e8bb5c43988ff9024fb4ce18b74145021462c4f5bc9c4a924925072666f73a12d1d2f1fef78a319a6b3e6aff6f9115bcbe6251145ec426486d179e5b334a4b5016dbac463c0a7b1d22f4422f78bd78145c2458b5ed279e8f1bfdbb8998a942142332e3a99a12e54d4ce5ab0256d
这个RSA给出了“n,p,e,c”是一种没有见过的类型,首先试着把n放到网站里分解一下,无果。观察题目名称和内容,其中p的值给的很奇怪末尾几个值都是0,再结合题目描述为“rsaRecov”(RSA修复?),可不可能是这个p是一个不完整的p需要通过算发去补全它?
再次打开了“CTF小白”师傅的博客:深入浅出RSA在CTF中的攻击套路,阅读完后知道了这道题属于“ Factoring with high bits known攻击”类,做题思路和我设想的差不多。这里恢复p用到的算法为“Coppersmith partial information attack算法”,有sage脚本可以使用:
n=0x9f29e3566a1b337a700ca6b7e89f6f1acf8ee440c73d2efdf4aa0c4688b1c595c45889c186e64bb456fb43992c2b10e0caf58008afa99d824f57b6945d13e20f10a521f228f2f5b248014792df94249787f250b2b7379f470986c53bcf4b12fe26b91bbb2f07c210ed6119f6c24d9e53b69107908c3c29f4c99ee5cb6d35953f5902a94209e5a71a2db8307b239881cfba8894c6291de5949b1e717b33752820c9e5151f77d1bd7ba352c318f1ad305b1965d025affe39a8445807146034217aa54ad9b58a6f283af887284abe43b99dca468ffec00ab82863eca861bc6e5662268fe87ab4c69bb345341bf82cce2926cda811441db474220450988219f9b9ad
p_fake = 0xc0e32ed2f316de2a56d1f281aa015f0ec18009f6cf059abfe2193eab865203714d420ef58ff167608f00af025720abca4b83a09d7bbd5f9d16effd8b44718438cb7f32098a6dc4603c29d24888ef99be8e8d14be482f5f603be3ebf676250545682d05b1f62c569e7051d6ed63bd4e452b3fd787000000000000000000000000
pbits = 1024
kbits = 130
pbar = p_fake & (2^pbits-2^kbits)
PR.<x> = PolynomialRing(Zmod(n))
f = x + pbar
x0 = f.small_roots(X=2^kbits, beta=0.4)[0] # find root < 2^kbits with factor >= n^0.3
print(hex(int(x0 + pbar)))
运行结果:0xc0e32ed2f316de2a56d1f281aa015f0ec18009f6cf059abfe2193eab865203714d420ef58ff167608f00af025720abca4b83a09d7bbd5f9d16effd8b44718438cb7f32098a6dc4603c29d24888ef99be8e8d14be482f5f603be3ebf676250545682d05b1f62c569e7051d6ed63bd4e452b3fd78731a221e5a59938a59fe5c3d3
接下来就是正常的RSA题目了,需要一提的是已知n和p想要获得q应该是q=n/p但是用计算机做除法存在误差,这里可以用“//”或者内建函数“divmod()”来进行精确除法,关于python中的除法可以参考sicofield师傅的Python中的除法博客。
import gmpy2
from Crypto.Util.number import bytes_to_long, long_to_bytes
def Decrypt(c,e,p,q):
L=(p-1)*(q-1)
d=gmpy2.invert(e,L)
n=p*q
m=gmpy2.powmod(c,d,n)
flag=str(m)
return flag
p=148339034563449618424396214756132765935045100601450629410000723319184997314669131235613039478675630615866868884760485652870970811956875349659253211264237829918588241145863660004436587137311114246639466899709875204683618968855987161017336105691323383669798327476250479758392167743887177212455356120212054449279
q=0xc0e32ed2f316de2a56d1f281aa015f0ec18009f6cf059abfe2193eab865203714d420ef58ff167608f00af025720abca4b83a09d7bbd5f9d16effd8b44718438cb7f32098a6dc4603c29d24888ef99be8e8d14be482f5f603be3ebf676250545682d05b1f62c569e7051d6ed63bd4e452b3fd78731a221e5a59938a59fe5c3d3
e=65537
c=0x93b38eff708ee7bd46bbda06a7c648e34d40f1f54a14f02f49dd5e7e8cd659c7f4f1dcea919c9c7b8cbb710b9af8192f60cfca0e51ae50834eec2a912004f2a772c80bbed96ad9524b4b027474ae7880e0d65400c7155da81707b6bc0f61d5405eea79ccaf77af71bb974e82b8e7cc83d594f38ce47e93afc5fca1a340dbd4acaaf091dac93d1069f544a1d734893f2dd7856e8bb5c43988ff9024fb4ce18b74145021462c4f5bc9c4a924925072666f73a12d1d2f1fef78a319a6b3e6aff6f9115bcbe6251145ec426486d179e5b334a4b5016dbac463c0a7b1d22f4422f78bd78145c2458b5ed279e8f1bfdbb8998a942142332e3a99a12e54d4ce5ab0256d
print (Decrypt(c,e,p,q))
print(long_to_bytes(int(Decrypt(c,e,p,q))))
FLAG:GUETCTF{This_ls_vu1neAble_RsA}
Simple ECC
题目描述:
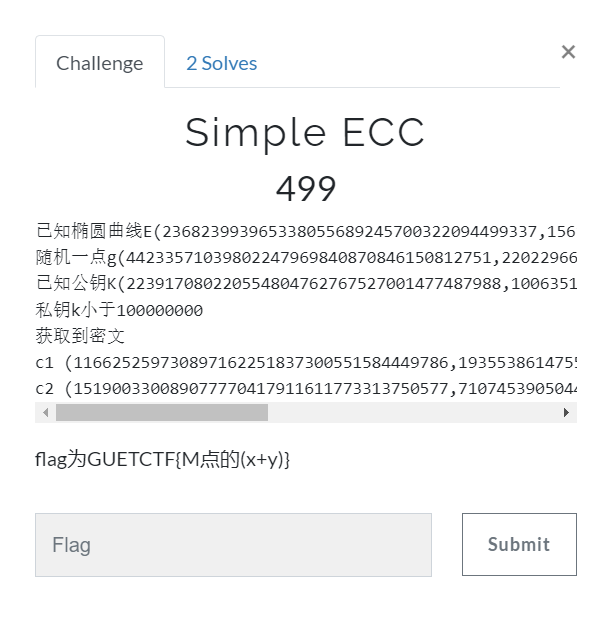
已知椭圆曲线E(236823993965338055689245700322094499337,156198018506580165174457632559424972017,166961927426036950608239191779402936500)
随机一点g(44233571039802247969840870846150812751,220229666726390439761711212813949151417)
已知公钥K(223917080220554804762767527001477487988,100635111839611507951802244486418487364)
私钥k小于100000000
获取到密文
c1 (116625259730897162251837300551584449786,193553861475567804708214612946951851888)
c2 (151900330089077770417911611773313750577,71074539050446765313176798346917980022)
又是ECC,但这次的ECC却没有给私钥k。没见过啊,怎么办呢?开始百度。
从百度上转了一圈下来并没有什么有用的发现,博客都只讲这么加密,不讲怎么解密。
没办法了,离比赛结束还有将近2.5h,干坐着也不是办法闲着也是闲着不如去尝试爆破一下这个ECC(理论存在实践开始):
a = 156198018506580165174457632559424972017
b = 166961927426036950608239191779402936500
M = 236823993965338055689245700322094499337
def add(A,B):
if A==(0,0): return B
if B==(0,0): return A
x1,y1 = A
x2,y2 = B
if A!=B:
p = (y2-y1)*pow(x2-x1,M-2,M)
else:
p = (3*x1*x1+a)*pow(2*y1,M-2,M)
x3 = p*p-x1-x2
y3 = p*(x1-x3)-y1
return (x3%M,y3%M)
base = (44233571039802247969840870846150812751,220229666726390439761711212813949151417)
pub = (223917080220554804762767527001477487988,100635111839611507951802244486418487364)
X = (0,0)
for i in range(M):
if X==pub:
secret = i
print ("secret:" + str(secret))
break
X = add(X, base)
print (i)
爆破脚本参考了Github上的一篇文章。文章里给出了py脚本和sage脚本,但在实际运行中sage脚本越运行越慢,为了能够更快的得出结果,我将py脚本使用pyinstaller工具打包成了.exe执行文件,这里主要参考了知乎@媳妇儿最大的别再问我怎么Python打包成exe了!经过将近1.5h的”鏖战“,爆破出了该题的k k = 67983944接下来通过sage脚本就能顺利得到flag了。
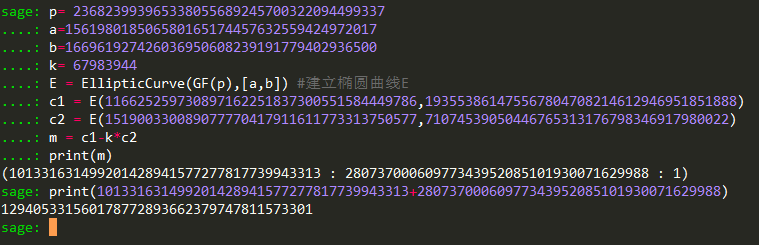
FLAG:GUETCTF{129405331560178772893662379747811573301}
写在最后
a.这是我参加的第一次ctf线下赛呢,AK了所有密码不戳不戳。但毕竟是校赛为了照顾大家在线下赛中加入了大块密码题,主流的线下赛中密码题的占比是不会这么大的,所以还需继续努力,考虑再向pwn或web发展一下;
b.赛后才知道那道ECC有相应的算法,毕竟CTF又不是在考验你的硬件设备,之后要学习一下ECC的相关攻击类型与解决方法再发一篇总结博客
c.本次的RSA是我没有见过的类型,其中的”Coppersmith partial information attack算法“我仅仅停留在使用脚本的水平,也需要去学习一下
作者:taotie
最后感谢一下我在解题过程中所观看的博客的作者,感谢师傅们产出的优质内容帮助我学习成长 阿里嘎多~


