62. 不同路径





class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
dp[0][0] = 1;
for (int i = 1; i < m; i++) {
dp[i][0] = 1;
}
for (int i = 1; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
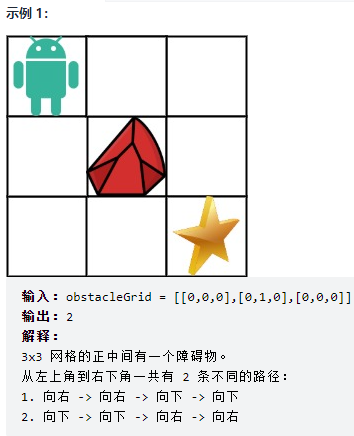
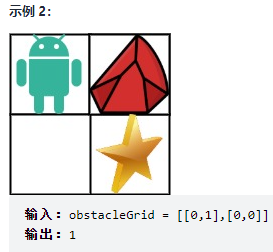
63. 不同路径 II


class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
if (obstacleGrid[0][0] == 1)
return 0;
dp[0][0] = 1;
for (int i = 1; i < m; i++) {
dp[i][0] = (obstacleGrid[i][0] == 1) ? 0 : dp[i - 1][0];
}
for (int i = 1; i < n; i++) {
dp[0][i] = (obstacleGrid[0][i] == 1) ? 0 : dp[0][i - 1];
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = (obstacleGrid[i][j] == 1) ? 0 : dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
64. 最小路径和



class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m][n];
dp[0][0] = grid[0][0];
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int i = 1; i < n; i++) {
dp[0][i] = dp[0][i - 1] + grid[0][i];
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
}
120. 三角形最小路径和





import java.util.List;
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[][] dp = new int[n][n];
int ans = Integer.MAX_VALUE;
dp[0][0] = triangle.get(0).get(0);
for (int i = 1; i < n; i++) {
for (int j = 0; j <= i; j++) {
if (j == 0) {
dp[i][j] = dp[i - 1][j] + triangle.get(i).get(j);
} else if (j == i) {
dp[i][j] = dp[i - 1][j - 1] + triangle.get(i).get(j);
} else {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);
}
}
}
for (int i = 0; i < n; i++) {
ans = Math.min(ans, dp[n - 1][i]);
}
return ans;
}
}
576. 出界的路径数

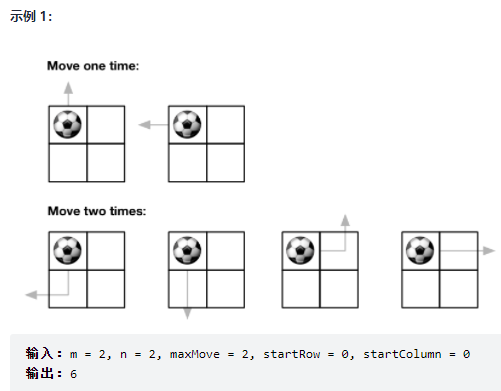
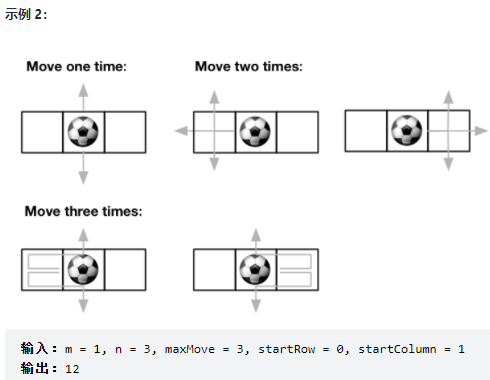

记忆化搜索
931. 下降路径最小和
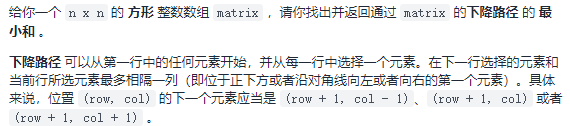


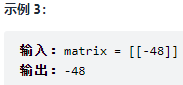

class Solution {
public int minFallingPathSum(int[][] matrix) {
int ans = Integer.MAX_VALUE;
int n = matrix.length;
for (int i = 0; i < n; i++) {
ans = Math.min(ans, find(matrix, i));
}
return ans;
}
private int find(int[][] matrix, int u) {
int n = matrix.length;
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
dp[0][i] = (i == u) ? matrix[0][i] : Integer.MAX_VALUE;
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = Integer.MAX_VALUE;
if (j == 0 && Math.min(dp[i - 1][j], dp[i - 1][j + 1]) != Integer.MAX_VALUE) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j + 1]) + matrix[i][j];
} else if (j == n - 1 && Math.min(dp[i - 1][j - 1], dp[i - 1][j]) != Integer.MAX_VALUE) {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + matrix[i][j];
} else {
if (j > 0 && j < n - 1 && Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i - 1][j + 1])) != Integer.MAX_VALUE)
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i][j];
}
}
}
int ans = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
ans = Math.min(ans, dp[n - 1][i]);
}
return ans;
}
}
class Solution {
public int minFallingPathSum(int[][] matrix) {
int n = matrix.length;
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
dp[0][i] = matrix[0][i];
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
if (j == 0) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j + 1]) + matrix[i][j];
} else if (j == n - 1) {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + matrix[i][j];
} else {
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i][j];
}
}
}
int ans = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
ans = Math.min(ans, dp[n - 1][i]);
}
return ans;
}
}
1289. 下降路径最小和 II



class Solution {
public int minFallingPathSum(int[][] grid) {
int n = grid.length;
int ans = Integer.MAX_VALUE;
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
dp[0][i] = grid[0][i];
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = Integer.MAX_VALUE;
}
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
if (k == j)
continue;
dp[i][j] = Math.min(dp[i][j], dp[i - 1][k] + grid[i][j]);
}
}
}
for (int i = 0; i < n; i++) {
ans = Math.min(ans, dp[n - 1][i]);
}
return ans;
}
}
1575. 统计所有可行路径



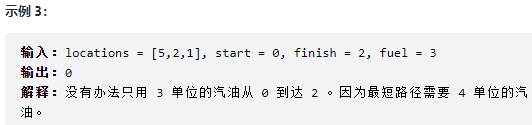
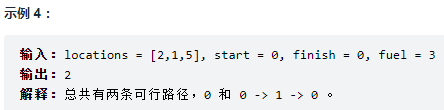
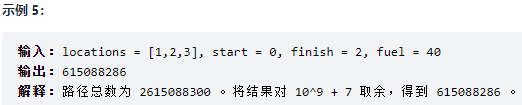

方法1 记忆化搜索
import java.util.Arrays;
class Solution {
int[][] cache;
public int countRoutes(int[] locations, int start, int finish, int fuel) {
cache = new int[locations.length][fuel + 1];
for (int i = 0; i < locations.length; i++) {
Arrays.fill(cache[i], -1);
}
return dfs(locations, start, finish, fuel);
}
private int dfs(int[] locations, int curCityId, int finish, int surplusFuel) {
if (cache[curCityId][surplusFuel] != -1)
return cache[curCityId][surplusFuel];
if (surplusFuel == 0 && curCityId != finish) {
cache[curCityId][surplusFuel] = 0;
return cache[curCityId][surplusFuel];
}
boolean hasNext = false;
for (int i = 0; i < locations.length; i++) {
if (i == curCityId)
continue;
int need = Math.abs(locations[i] - locations[curCityId]);
if (surplusFuel >= need) {
hasNext = true;
break;
}
}
if (surplusFuel != 0 && hasNext == false) {
cache[curCityId][surplusFuel] = (curCityId == finish) ? 1 : 0;
}
int sum = (curCityId == finish) ? 1 : 0;
for (int i = 0; i < locations.length; i++) {
if (i == curCityId)
continue;
int need = Math.abs(locations[i] - locations[curCityId]);
if (surplusFuel >= need) {
sum += dfs(locations, i, finish, surplusFuel - need);
sum %= 1000000007;
}
}
cache[curCityId][surplusFuel] = sum;
return sum;
}
}
方法2 动态规划
class Solution {
public int countRoutes(int[] locations, int start, int finish, int fuel) {
int cityNum = locations.length;
int[][] dp = new int[cityNum][fuel + 1];
for (int i = 0; i < fuel + 1; i++) {
dp[finish][i] = 1;
}
for (int cur = 0; cur <= fuel; cur++) {
for (int i = 0; i < cityNum; i++) {
for (int k = 0; k < cityNum; k++) {
if (k == i)
continue;
int need = Math.abs(locations[i] - locations[k]);
if (cur >= need) {
dp[i][cur] += dp[k][cur - need];
dp[i][cur] %= 1000000007;
}
}
}
}
return dp[start][fuel];
}
}



