树、二叉树、查找算法总结

一.思维导图

1.树

2.二叉树

3.查找

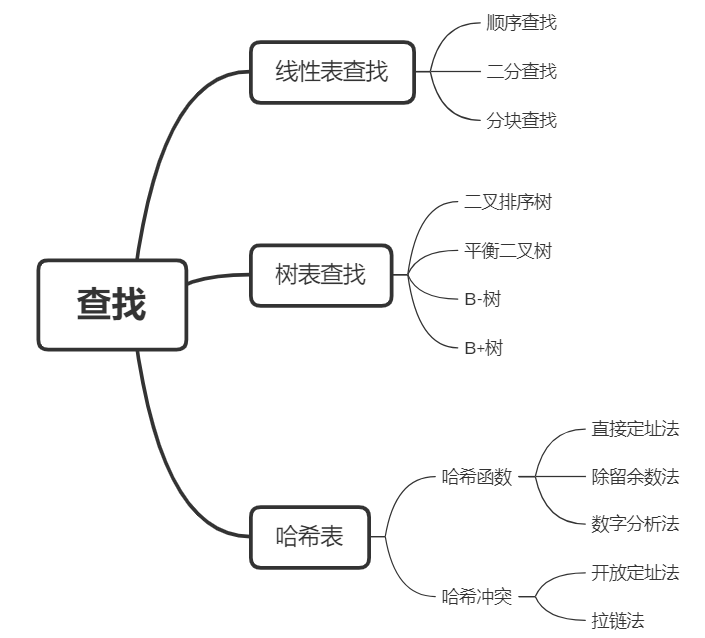
二.重要概念

1.度

结点的子树的个数称为该结点的度，一个树中所有结点的度中的最大值称为树的度。

2.二叉树的性质

(1) 在非空二叉树中，第i层的结点总数不超过, i>=1。
(2) 深度为h的二叉树最多有个结点(h>=1)，最少有h个结点。
(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1。

3.确认左右孩子

有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：
若I为结点编号则 如果I>1，则其父结点的编号为I/2
如果2I<=N，则其左孩子（即左子树的根结点）的编号为2I；若2I>N，则无左孩子
如果2I+1<=N，则其右孩子的结点编号为2I+1；若2I+1>N，则无右孩子

4.遍历

先序

⑴访问根结点
⑵遍历左子树
⑶遍历右子树

中序

⑴遍历左子树
⑵访问根结点
⑶遍历右子树

后序

⑴遍历左子树
⑵遍历右子树
⑶访问根结点

5.森林、树转换为二叉树

森林转二叉树：将森林中的每棵树变为二叉树，将各二叉树的根结点视为兄弟从左至右连在一起，就形成了一棵二叉树。
树转二叉树：在所有兄弟结点之间加一连线，对每个结点除了保留与其长子的连线外，去掉该结点与其它孩子的连线。

6.哈夫曼树

带权路径长度WPL最小的二叉树称为哈夫曼树。
WPL=所有（叶子结点的权值*路径长度）之和

7.哈希表

除留余数法：

h(k)=m%p(p为素数，p<=m)

装填因子a：

装填因子是指哈希表中已存入的元素数n与哈希表地址空间大小的比值，即a=n÷m，通常a控制在0.6到0.9的范围内。

三.疑难问题

ASL

上完课后对哈希表的ASLASL不成功这块不是很理解，于是我在网上查找了一些资料
解决：首先ASL的定义是

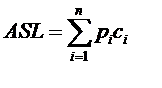
其中n为查找表中元素个数，Pi为查找第i个元素的概率，Ci是找到第i个元素的比较次数。
网上有一题关于哈希表成功与不成功解法的例题：
将关键字序列（7、8、30、11、18、9、14）散列存储到散列表中。散列表的存储空间是一个下标从0开始的一维数组。散列函数为： H(key) = (keyx3) MOD 7，处理冲突采用线性探测再散列法，要求装填（载）因子为0.7。
(1) 请画出所构造的散列表；
(2) 分别计算等概率情况下查找成功和查找不成功的平均查找长度。
1.散列表：
α = 表中填入的记录数/哈希表长度 ==> 哈希表长度 = 7/0.7 = 10
H(7) = (7x3) MOD 7 = 0 H(8) = (8x3) MOD 7 = 3 H(30) = (30x3) MOD 7 = 6
H(11) = (11x3) MOD 7 = 5 H(18) = (18x3) MOD 7 = 5 H(9) = (9x3) MOD 7 = 6
H(14) = (14x3) MOD 7 = 0
按关键字序列顺序依次向哈希表中填入，发生冲突后按照“线性探测”探测到第一个空位置填入。
0 1 2 3 4 5 6 7 8 9
7 14 8 11 30 18 9
2.查找长度：
2.1 查找成功的平均查找长度
（待查找的数字肯定在散列表中才会查找成功）
查找数字A的长度 = 需要和散列表中的数比较的次数；
步骤：
比如 查找数字：8
则 H(8) = (8x3) MOD 7 = 3
哈希表中地址3处的数字为8，进行了第一次比较：8 = 8，则查找成功，查找长度为1；
比如查找数字：14
则 H(14) = (14x3) MOD 7 = 0
哈希表中地址0处的数字为7，进行第一次比较：7≠14
哈希表中地址1处的数字为14，进行第二次比较：14=14 ，则查找成功，查找长度为2。
由此可得到如下数据：【2016年12月26日修改，多谢@一楼的朋友指正】
0 1 2 3 4 5 6 7 8 9
7 14 8 11 30 18 9
1 2 1 1 1 3 3
所以总的查找成功的平均查找长度= （1+1+1+1+3+3+2）/7 = 12/7
2.2查找不成功的平均查找长度
（待查找的数字肯定不在散列表中）
【解题的关键之处】根据哈希函数地址为MOD7，因此任何一个数经散列函数计算以后的初始地址只可能在0~6的位置
查找0~6位置查找失败的查找次数为：
地址0，到第一个关键字为空的地址2需要比较3次，因此查找不成功的次数为3.
地址1，到第一个关键字为空的地址2需要比较2次，因此查找不成功的次数为2.
地址2，到第一个关键字为空的地址2需要比较1次，因此查找不成功的次数为1.
地址3，到第一个关键字为空的地址4需要比较2次，因此查找不成功的次数为2.
地址4，到第一个关键字为空的地址4需要比较1次，因此查找不成功的次数为1.
地址5，到第一个关键字为空的地址2(比较到地址6，再循环回去)需要比较5次，因此查找不成功的次数为5.
地址6，到第一个关键字为空的地址2(比较到地址6，再循环回去)需要比较4次，因此查找不成功的次数为4.
于是得到如下数据：
0 1 2 3 4 5 6 7 8 9
7 14 8 11 30 18 9
3 2 1 2 1 5 4
则查找不成功的平均查找长度 = （3+2+1+2+1+5+4）/7 = 18/7