浅谈双连通分量、强连通分量

        初谈这个话题相信每一位都会感到一丝疑惑，主要原因是这个词中“分量”一词，当然，如果仅是为了了解和使用这两个术语，就不必在意这个无关大体的词语。

        好了，该谈谈正题了，所谓双连通与强连通，最大的差别，也是最本质的差别就是前者适用于无向图中，而后者适用于有向图。至于两者的概念是一样的，就是图中有a点、b点，从a点可到达b点，同时从b点可到达a点。（若是有向图必须延方向到达。）

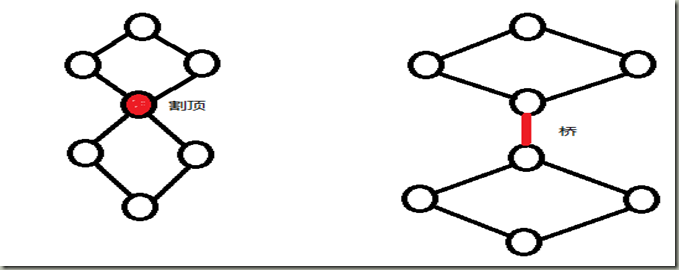
        其中双连通分量可细分为：点-双连通分量，边-双连通分量。所谓点-双连通分量是指在一个无向图中两点间至少有两条路径，且路径中（不算头尾）的点不同。不同的点-双连通分量最多有一个公共点，这个点必定是“割顶”。提到割顶不得不在这里啰嗦一下，割顶（如下图）就是当删去这个点时，连通块的数量会增加。至于什么叫连通块，可以理解为一个点的集合，若两点间可直接或间接的连接则两点在同一连通块中。

至于边-双连通分量是指在一个无向图中两点间至少有两条路径，且路径中的边不同。边-双连通分量中一定没有桥。而桥（如上图）是指当删去这个边时，连通块的数量会增加。

       知识性的东西已经科普完了，下面大致说一下程序。

判断无向连通图是否连通：

void dfs(int v)
{
      node_pointer w;
     visited[v] = TRUE;
     for(w = graph[v]; w; w = w->link)
    {
         if(!visited[w->vertex])
        {
              dfs(w->vertex);
        }
    }
}
void connect()
{
     for(int i = 0; i < n; i++)
    {
         if(!visited[i]) 
        {
              dfs(i);
        }
    }
}

求点-双连通图：

stack<int> s; 
int num=1,time=0;
int id[1000]={0}; 

void tarjan(int x, int fa)
{
    dfn[x]=low[x]=time++; 
    for(int e=first[x];e!=-1;e=next[e])
    { 
        if(x!=fa&&dfn[x]<dfn[v[e]])
        {
            s.push(e); 
            
            if(dfn[x]==0)
            {
                  tarjan(v[e], x);
                  if(low[v[e]]<low[x])   low[x]=low[v[e]]; 
                  if(low[v[e]]>=dfn[x])
                  { 
                      int edge; 
                      do
                      { 
                          s.pop();
                          edge=s.top();
                          id[u[edge]]=id[v[edge]]=num++;
                      }while(u[edge]!=x||v[edge]!=v[e]);
                  }
            } 
            else if(dfn[v[e]]<low[x]) low[x]=dfn[v[e]]; 
        }
    }
}

求边-双连通图：

void(int u,int fa)
{ 
    dfn[u]=low[u]=++time;
    s[top++]=u; 
    
    for(int e=first[u];e!=-1;e=next[e]) 
    {
        if(v[e]!=fa)
        { 
            if(!dfn[v[e]])
            {
                tarjan(v[e],u); 
                
                if(low[v[e]]<low[u])  low[u]=low[v[e]]; 
                else if(low[v[e]]>dfn[u])
                { 
                    for(s[top]=-1;s[top]!=v[e];)
                    {
                        id[s[--top]]=num;
                        num++;
                    }
                }
            } 
            else if(dfn[v[e]]<low[u])  low[u]=dfn[v[e]];
        }
    }
}

求强连通图：

void tarjan(int i)
{
    int j;
    DFN[i]=LOW[i]=++Dindex;
    instack[i]=true;
    Stap[++Stop]=i;
    
    for (edge *e=V[i];e;e=e->next)
    {
        j=e->t;
        if (!DFN[j])
        {
            tarjan(j);
            if (LOW[j]<LOW[i])  LOW[i]=LOW[j];
        }
        else if (instack[j] && DFN[j]<LOW[i])  LOW[i]=DFN[j];
    }
    
    if (DFN[i]==LOW[i])
    {
        Bcnt++;
        do
        {
            j=Stap[Stop--];
            instack[j]=false;
            Belong[j]=Bcnt;
        }while (j!=i);
    }
}
void solve()
{
    Stop=Bcnt=Dindex=0;
    
    memset(DFN,0,sizeof(DFN));
    
    for (int i=1;i<=N;i++)
    {
        if (!DFN[i])  tarjan(i);
    }
}

感谢各位观看我的博客，如有不足欢迎提出，同时希望你们能有所收获，谢谢。