哈尔滨工业大学计算机学院-模式识别-课程总结(五)-成分分析
1. 成分分析
常用的成分分析有PCA和FDA,本章主要介绍主成分分析PCA,对于FDA,只是简要介绍其主要数学思想。
进行成分分析的目的是对数据集特征进行降维,降维的好处有:
- 减少计算量
- 提高泛化能力:减少模型的参数数量。往往数据特征维度越高,模型越容易过拟合。
融入核函数的SVM,虽然是在高维特征空间下学习分类界面,但是由于SVM的VC维受分类界面与样本控制,因此不会增大其VC维,也就不会降低模型的泛化能力。
2. 主成分分析PCA
- PCA:一种最常用的线性成分分析方法。
- PCA的主要思想:寻找到数据的主轴方向,由主轴构成一个新的坐标系(维数可以比原维数低),然后数据由原坐标系向新的坐标系投影。
- PCA的其它名称:离散K-L变换,Hotelling变换。
PCA从尽量减少信息损失的角度实现降维。
2.1 PCA坐标变换说明
- 坐标变换过程:
\[\begin{array} { c } { \mathbf { x } = \mathbf { \mu } + \mathbf { x } ^ { \prime } } \\ { \mathbf { x } = \boldsymbol { \mu } + \sum _ { i = 1 } ^ { d } a _ { i } \mathbf { e } _ { i } } \\ { \hat { \mathbf { x } } = \mathbf { \mu } + \sum _ { i = 1 } ^ { d ^ { \prime } } a _ { i } \mathbf { e } _ { i } } \end{array}
\]
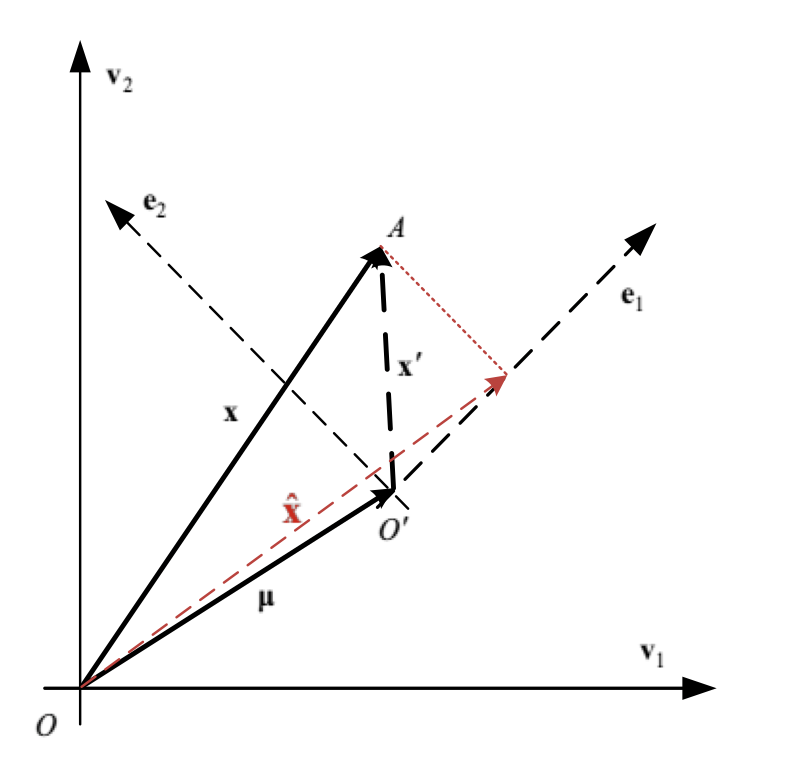
- PCA的优化问题: \(\min _ { \mathbf { e } _ { 1 } , \cdots , \mathbf { e } _ { d } } J \left( \mathbf { e } _ { 1 } , \cdots , \mathbf { e } _ { d } \right) = \frac { 1 } { n } \sum _ { k = 1 } ^ { n } \left\| \mathbf { x } _ { k } - \hat { \mathbf { x } } _ { k } \right\| ^ { 2 }\)
如图所示,坐标A降维到新的坐标系下红色虚线指向的一维坐标。(选择\(e_1\)作为新坐标系的基向量)
2.2 PCA算法
- PCA算法的过程(这里只介绍结果,没有数学证明过程):
- 利用训练样本集合计算样本的均值\(\mu\)和协方差矩阵\(\Sigma\).
- 计算\(\Sigma\)的特征值,并由大到小排序。
- 选择前\(d^′%个特征值对应的特征矢量作成一个变换矩阵\)E=[e_1, e_2, …, e_(d^′ )]$。
- 训练和识别时,每一个输入的\(d\)维特征矢量\(x\)可以转换为\(d^′\)维的新特征矢量\(y\):
\[\mathbf { y } = \mathbf { E } ^ { t } ( \mathbf { x } - \mathbf { \mu } )
\]
2.3 PCA算法特点
- 正交性:由于\(\Sigma\)是实对称阵,因此特征矢量是正交的。
- 不相关性:将数据向新的坐标轴投影之后,特征之间是不相关的。
- 特征值:描述了变换后各维特征的重要性,特征值为0的各维特征为冗余特征,可以去掉。
3. 基于Fisher准则的线性判别分析FDA
- PCA是典型的无监督算法,但是我们降维的目的往往是为了后续步骤的进一步分类。PCA因为其无监督的特点,将所有的样本作为一个整体对待,寻找一个平方误差最小意义下的最优线性映射,而没有考虑样本的类别属性。因此在降维的过程中,尽管是沿着信息损失最少的方向,但也有可能就会把类别信息丢失。
- 在下图的例子中,二维数据如果沿着\(e_1\)特征方向进行降维,会完全丢失类别信息。
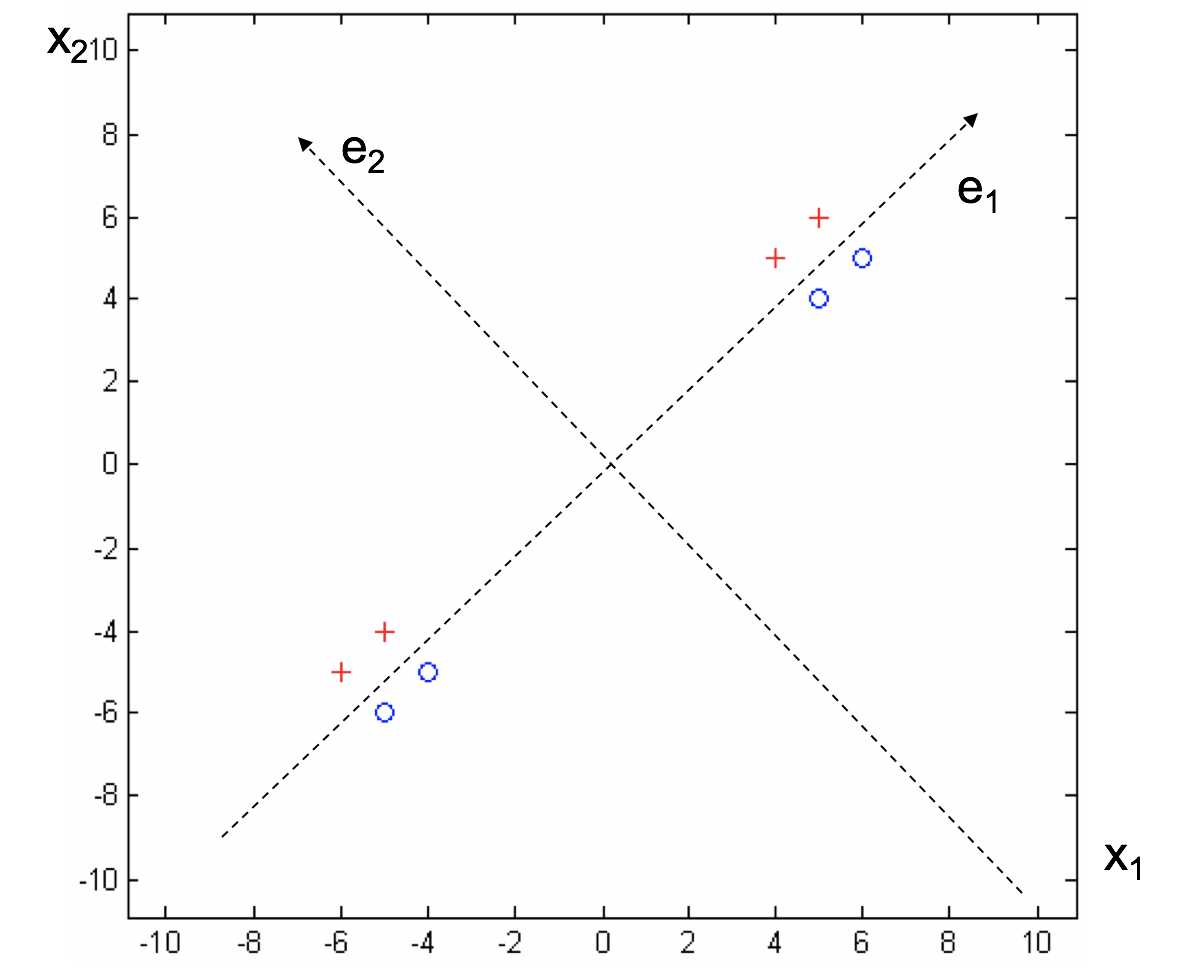
- 而FDA则是在可分性最大意义下的最优线性映射,充分保留了样本的类别可分性信息。
3.1 FDA可视化
- 三类问题的FDA可视化:
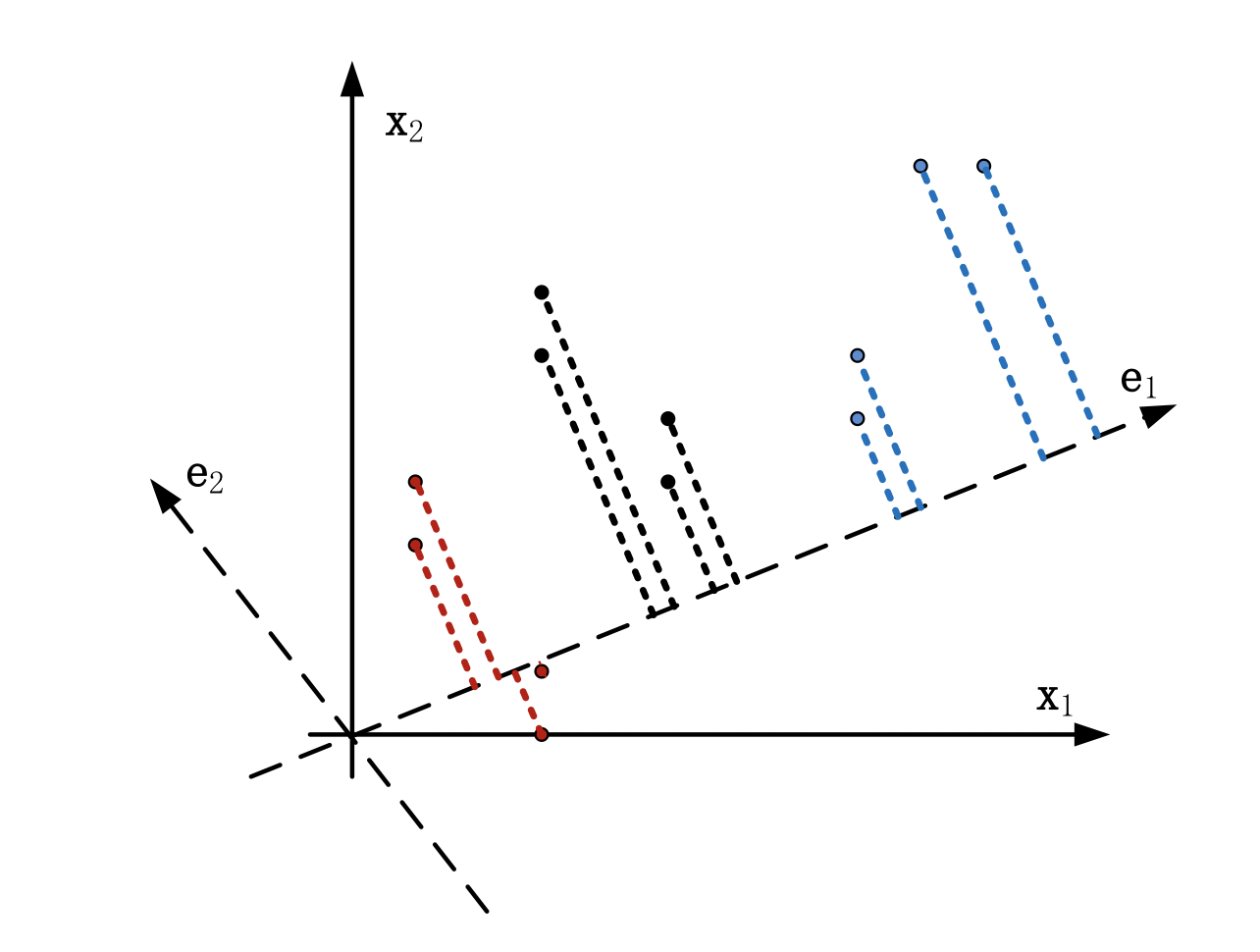
3.2 FDA算法特点
- 非正交:经FDA变换后,新的坐标系不是一个正交坐标系。
- 特征维数:新的坐标维数最多为\(c-1\),\(c\)为类别数。




