哈尔滨工业大学计算机学院-模式识别-课程总结（三）-线性判别函数

1. 线性判别函数

• 本章介绍的线性判别函数都归属于判别式模型，即对于分类问题，根据判别函数\(g(x)\)的取值进行判断，比如正数归为第一类，负数与零归为第二类。关于判别式模版与生成式模型的区别可以阅读我以前的博客，最典型的生成式模型是贝叶斯分类器，这个在之前的博客中也有介绍。
• 在介绍具体算法之前，先了解一下线性判别函数的基本概念。

1.2 线性判别函数基本概念

• 对于线性可分情况，线性判别函数\(g(x)\)与判别界面\(H\)如下图所示：
  
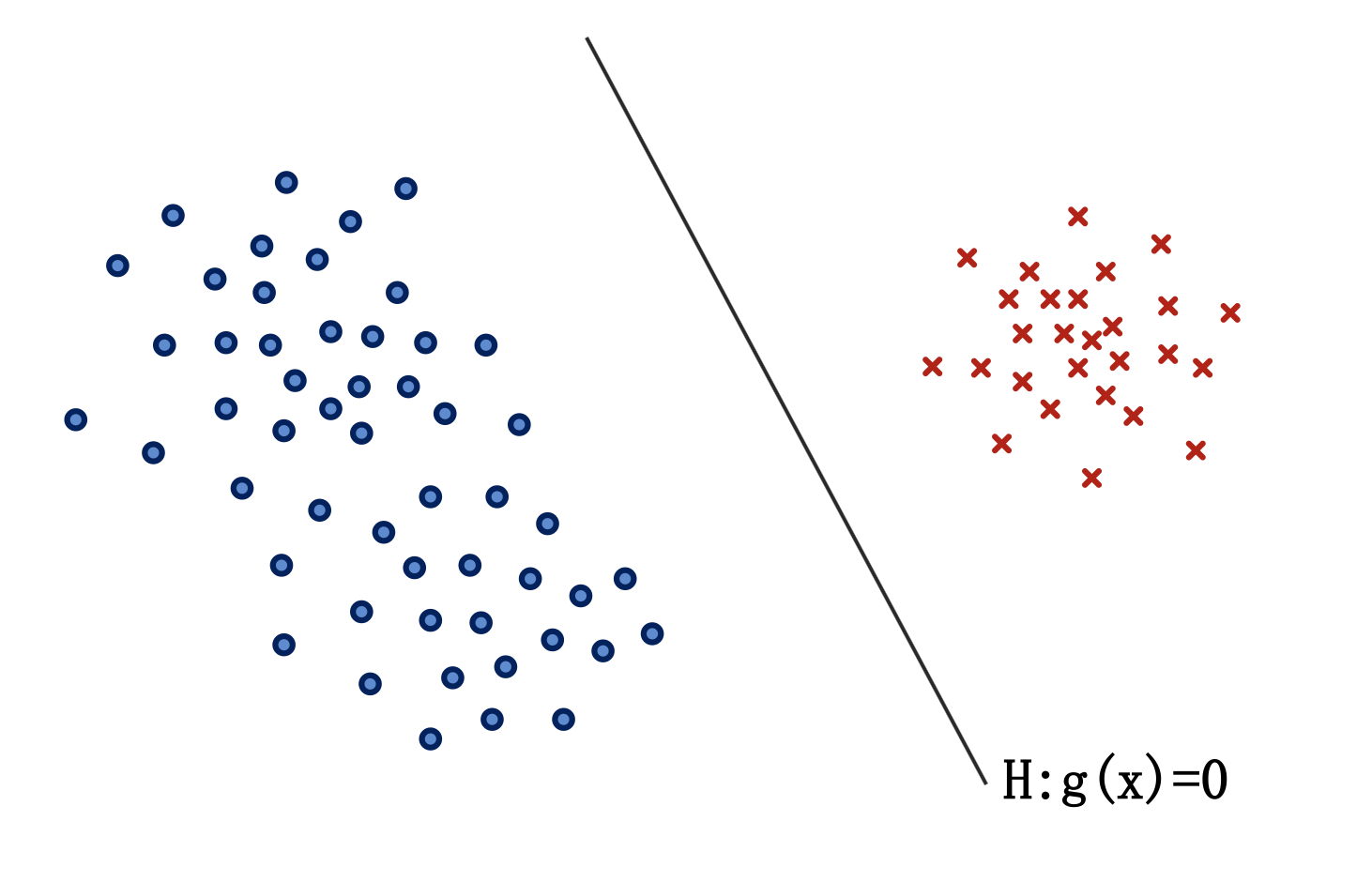
• 对于线性不可分情况：
  
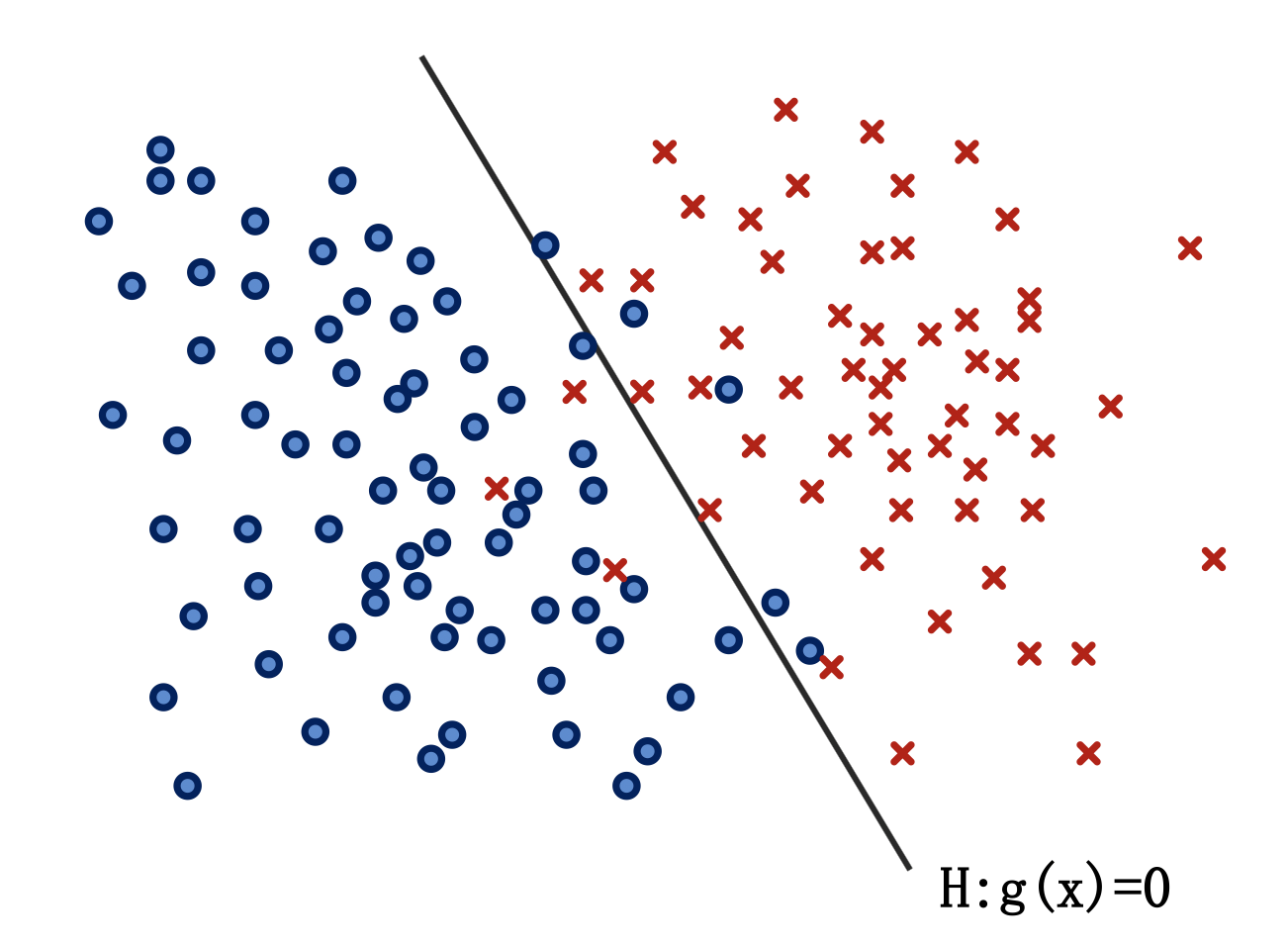
• 线性判别函数的形式化形式为：

\[g ( \mathbf { x } ) = \mathbf { w } ^ { t } \mathbf { x } + w _ { 0 } \]

• \(\mathbf { x } = \left( x _ { 1 } , x _ { 2 } , \ldots , x _ { d } \right) ^ { t }\)，是特征矢量，\(d\)是特征维度的大小。
• \(\mathbf { w } = \left( w _ { 1 } , W _ { 2 } , \dots , W _ { d } \right) ^ { t }\)，是权矢量。
• \(W _ { 0 }\) 是偏置。
• 线性判别函数的增广形式（便于书写，便于设计目标函数）：

\[g ( \mathbf { y } ) = \mathbf { a } ^ { t } \mathbf { y } \]

• \(\mathbf { y } = \left( 1 , x _ { 1 } , x _ { 2 } , \ldots , x _ { d } \right) ^ { t }\)，是增广的特征矢量，在原始向量前插\(1\)即可。
• \(\mathbf { a } = \left( w _ { 0 } , w _ { 1 } , W _ { 2 } \dots , W _ { d } \right) ^ { t }\)，是增广的权矢量。

在学习该增广形式的时候，我曾思考过，既然可以将将线性函数转化为两个向量的点乘，那在深度学习中(以pytorch为例)，设计线性层(nn.Linear)时为什么还要令参数bias=True，直接不需要偏置，在输入向量中拼接一个维度(值为1)岂不是更加方便。答案当然是否定，我仔细思考后发现，如果这么做的话，对于每一个输入对会有一个独立的bias，因为新拼接的“1”值会随着反向传播进行迭代更新（每个输入的更新结果不同），此时bias便失去了意义，不再是与线性函数函数绑定，而是变成了输入的一个特征。

• 两类问题的线性判别准则：

\[g ( \mathbf { x } ) = \mathbf { w } ^ { t } \mathbf { x } + w _ { 0 } \left\{ \begin{array} { l l } { > 0 , } & { \mathbf { x } \in \omega _ { 1 } } \\ { < 0 , } & { \mathbf { x } \in \omega _ { 2 } } \\ { = 0 } & {拒识 } \end{array} \right. \]

• 线性分类器的分类界面三维空间可视化：
  

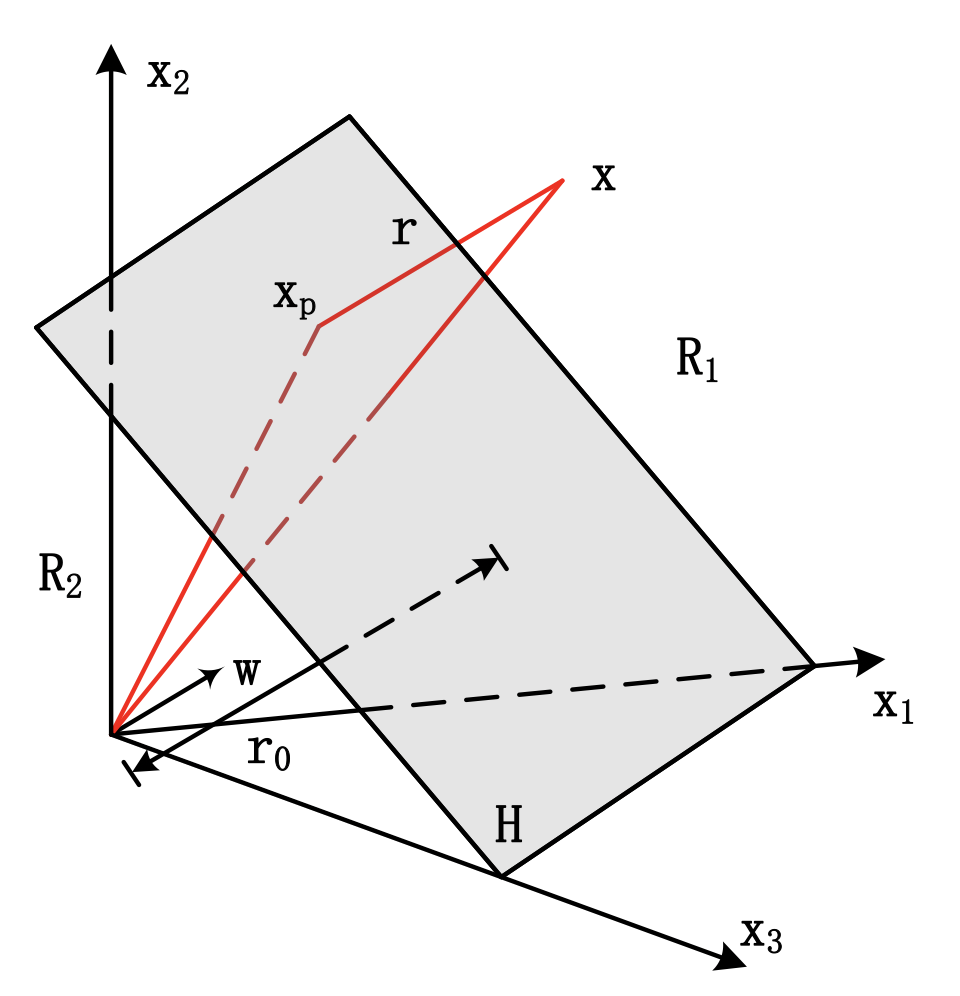
  该界面有几个特点：
  1.线性分类界面\(H\)是\(d\)维空间中的一个超平面；
  2.分类界面将\(d\)维空间分成两部分，\(R_1\)，\(R_2\)分别属于两个类别；
  3.判别函数的权矢量\(w\)是一个垂直于分类界面\(H\)的矢量，其方向指向区域\(R_1\) ；
  4.偏置\(w_0\)与原点到分类界面\(H\)的距离\(r_0\)有关：

  \[r _ { 0 } = \frac { w _ { 0 } } { \| \mathbf { w } \| } \]

1.3 线性判别函数的学习

• 以下内容全部采用增广形式的写法进行介绍。
• 线性判别函数的学习目的，其实就是想通过\(n\)个训练样本\(\mathbf { y } _ { 1 } , \mathbf { y } _ { 2 } , \dots , \mathbf { y } _ { n }\)，来确定一个判别函数\(g ( \mathbf { y } ) = \mathbf { a } ^ { t } \mathbf { y }\)的权矢量\(a\)。其中n个样本集合来源于两个不同类别。
  • 在线性可分的情况下，希望得到的判别函数能够将所有的训练样本正确分类。
  • 线性不可分的情况下，判别函数产生错误的概率最小。
• 判别函数的非规范化形式：

\[\left\{ \begin{array} { l l } { \mathbf { a } ^ { t } \mathbf { y } _ { i } > 0 , } & { \mathbf { y } _ { i } \in \omega _ { 1 } } \\ { \mathbf { a } ^ { t } \mathbf { y } _ { i } < 0 , } & { \mathbf { y } _ { i } \in \omega _ { 2 } } \end{array} \right. \]

• 判别函数的规范化i形式：

\[\left\{ \begin{array} { c l } { \mathbf { a } ^ { t } \mathbf { y } _ { i } > 0 , } & { \mathbf { y } _ { i } \in \omega _ { 1 } } \\ { - \mathbf { a } ^ { t } \mathbf { y } _ { i } > 0 , } & { \mathbf { y } _ { i } \in \omega _ { 2 } } \end{array} \right. \]

• 在之后的感知器算法、 LMSE中，均依据规范化的形式进行介绍，规范化后会使得目标函数形式比较简单。
• 规范化是在输入数据上进行，将属于第二个类别的数据乘上\(-1\)即可。
• 需要注意，因为本节内容是在函数的增广形式下进行介绍，因此在规范化之前需要对于每个类别的数据都拼接一个特征“1”。

2. 二分类问题

这里介绍常用的线性分类函数，感知器、LMSE和SVM，其中SVM本身是线性分类器，但当其加入核函数之后可以达到非线性分类器的效果，实践中我们经常使用的也是非线性SVM，关于核函数的概念会在后续博客中介绍。

2.1 感知器算法Perception

在介绍感知器算法之前，先了解一下什么是感知器准则。

2.1.1 感知器准则

• 显然对于分类问题，最直观的准则函数定义是最少错分样本数准则：

\[J _ { N } ( \mathbf { a } ) =样本集合中被错误分类的样本数 \]

• 其函数可视化形式如下：
• 
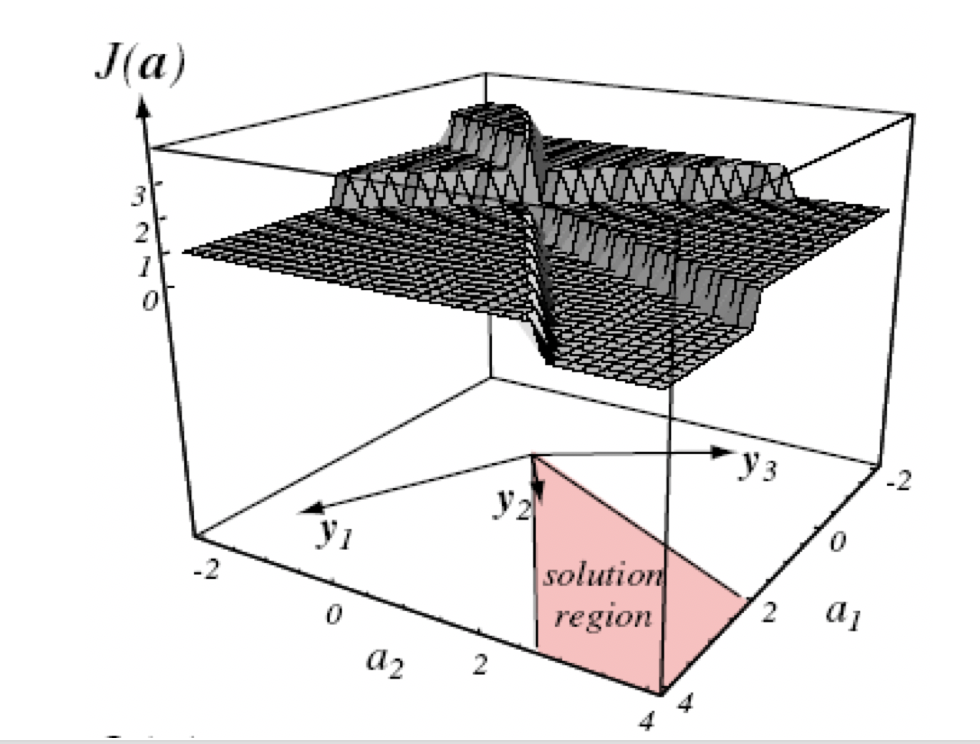
• 由于该函数是分段常数函数，不便于采用梯度下降的学习策略进行学习，因此该准则不是一个好的选择。
• 更好的感知器准则函数定义如下所示（著名的感知器准则）：

\[J _ { P } ( \mathbf { a } ) = \sum _ { \mathbf { y } \in \mathcal { Y } } \left( - \mathbf { a } ^ { t } \mathbf { y } \right) \]

\[\nabla J _ { P } = \sum _ { \mathbf { y } \in \mathcal { Y } } ( - \mathbf { y } ) \]

• 其函数可视化形式如下：
• 
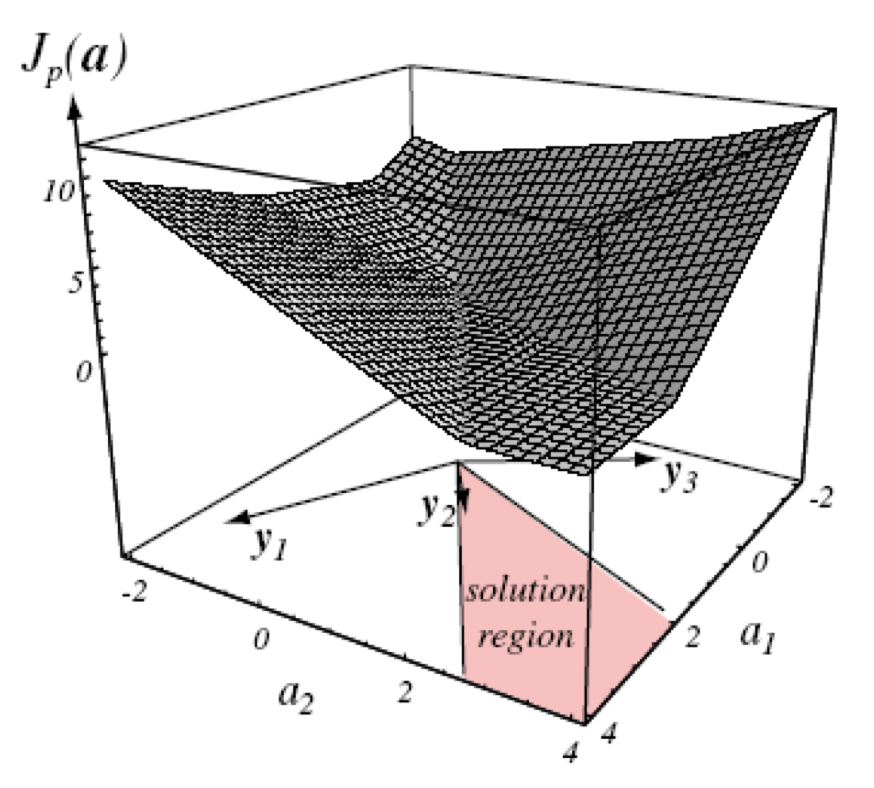
• 个人认为该准则最大的好处是梯度函数比较直观，而且容易计算，适用于梯度下降学习策略。
• 更加细节的感知器训练方式，会在后续的实验中进行详细介绍，并开源实验代码。

2.1.2 感知器算法的特点

• 感知器算法的特点如下：
  • 当样本线性可分情况下，学习率合适时，算法具有收敛性。
  • 收敛速度较慢。
  • 当样本线性不可分情况下，算法不收敛，且无法判断样本是否线性可分。

2.2 最小平方误差算法LMSE

• 如2.1所说，感知器算法对于线性可分问题能够得到很好的结果，但是对于线性不可分问题往往不能收敛。按照正常人的思考，即使是对于一个线性不可分问题，我们也希望线性判别函数能够得到一个“错误最小”的解，而不应该是算法无法收敛的程度。
• 基于这种思想，我们得到了一个在线性可分和线性不可分条件下都有很好性能的折衷算法LMSE。
• LMSE将求解线性不等式组的问题转化为求解线性方程组。所谓线性不等式组便是1.3中介绍的规范化后判别函数不等式组。我们希望每个不等式都是大于0的，既然这样，LMSE设定了任意的正常数\(b\)，将不等式转化为等式，只要等式成立，那左边的多项式一定是大于0的。
• LMSE的函数形式如下所示：

\[\left( \begin{array} { c c c c } { y _ { 10 } } & { y _ { 11 } } & { \cdots } & { y _ { 1 d } } \\ { y _ { 20 } } & { y _ { 21 } } & { \cdots } & { y _ { 2 d } } \\ { \vdots } & { \vdots } & { \ddots } & { \vdots } \\ { y _ { n 0 } } & { y _ { n 2 } } & { \cdots } & { y _ { n d } } \end{array} \right) \left( \begin{array} { c } { a _ { 0 } } \\ { a _ { 1 } } \\ { \vdots } \\ { a _ { d } } \end{array} \right) = \left( \begin{array} { c } { b _ { 1 } } \\ { b _ { 2 } } \\ { \vdots } \\ { b _ { n } } \end{array} \right) \]

• 可简化写为：

\[\mathbf { Y } \mathbf { a } = \mathbf { b } , \quad \mathbf { b } > 0 \]

2.2.1 LMSE的准则函数

• 定义误差矢量\(e\)，用\(e\)长度的平方作为准则函数：

\[\begin{array} { c } { \mathbf { e } = \mathbf { Y } \mathbf { a } - \mathbf { b } } \\ { J _ { S } ( \mathbf { a } ) = \| \mathbf { Y } \mathbf { a } - \mathbf { b } \| ^ { 2 } } \end{array} \]

• 我们想该准则函数越小越好，这样不等式的值就越接近于正常数\(b\)的值，也就达到了不等式组恒为正的目的。

2.2.2 LMSE的求解过程

• LMSE求解的目的是得到符合要求的权矢量\(a\)。
• 求解方法分为两种：伪逆求解法与迭代求解法。
• 伪逆求解法：
  • LMSE准则其实就是误差平方和最小问题，属于经典的数学问题。伪逆求解法其实是令准则函数\(J _ { S } ( \mathbf { a } )\)梯度值为0，从而计算得到一个必要条件。
  • 利用数学公式推导，得到权矢量的解析解。

\[\begin{array} { c } { \nabla J _ { S } ( \mathbf { a } ) = 2 \mathbf { Y } ^ { t } ( \mathbf { Y } \mathbf { a } - \mathbf { b } ) = \mathbf { 0 } } \\ { \mathbf { Y } ^ { t } \mathbf { Y } \mathbf { a } = \mathbf { Y } ^ { t } \mathbf { b } } \\ { \mathbf { a } = \left( \mathbf { Y } ^ { t } \mathbf { Y } \right) ^ { - 1 } \mathbf { Y } ^ { t } \mathbf { b } = \mathbf { Y } ^ { + } \mathbf { b } } \end{array} \]

• \(\mathbf { Y } ^ { + } = \left( \mathbf { Y } ^ { t } \mathbf { Y } \right) ^ { - 1 } \mathbf { Y } ^ { t }\)称为伪逆矩阵。
• 之所以这么做是因为输入矩阵\(Y\)往往是奇异矩阵，也就是不可逆的，因此采用上述的伪逆求解方式。
• 需要注意的是，\(\mathbf { Y } ^ { t } \mathbf { Y }\)当样本数多的时候一般是可逆的，当特征数大于样本数时，基本是不可逆的，也就不能采用这种伪逆求解法。
• 迭代求解法：
  • 对于准则函数\(J _ { S } ( \mathbf { a } )\)的进一步计算为：

\[J _ { s } ( \mathbf { a } ) = \| \mathbf { Y } \mathbf { a } - \mathbf { b } \| ^ { 2 } = \sum _ { i = 1 } ^ { n } \left( \mathbf { a } ^ { \prime } \mathbf { y } _ { i } - b _ { i } \right) ^ { 2 } \]

• 准则函数的梯度为：

\[\boldsymbol { \nabla } J _ { s } = \sum _ { i = 1 } ^ { n } 2 \left( \mathbf { a } ^ { \prime } \mathbf { y } _ { i } - b _ { i } \right) \mathbf { y } _ { i } \]

• 迭代求解法就是采用梯度下降的方式进行实现，具体学习过程在后学的实验博客中进行介绍。

• 迭代求解过程中往往省略掉梯度中的系数\(2\)，因为该数值可以整合进学习率中。

• 实践过程中，伪逆求解法的效果不如迭代求解法效果好

2.2.3 LMSE算法的特点

• 算法的收敛程度依赖于学习率的衰减。
• 算法对于线性不可分的训练样本也能够收敛于一个均方误差最小解。
• 取\(b=1\)时，当样本数趋于无穷多时，算法的解以最小均方误差逼近贝叶斯判别函数。
• 当训练样本线性可分的情况下，算法未必收敛于一个分类超平面。
  • LMSE在线性可分的问题中，得到的效果不是很好，举例如下：
  • 

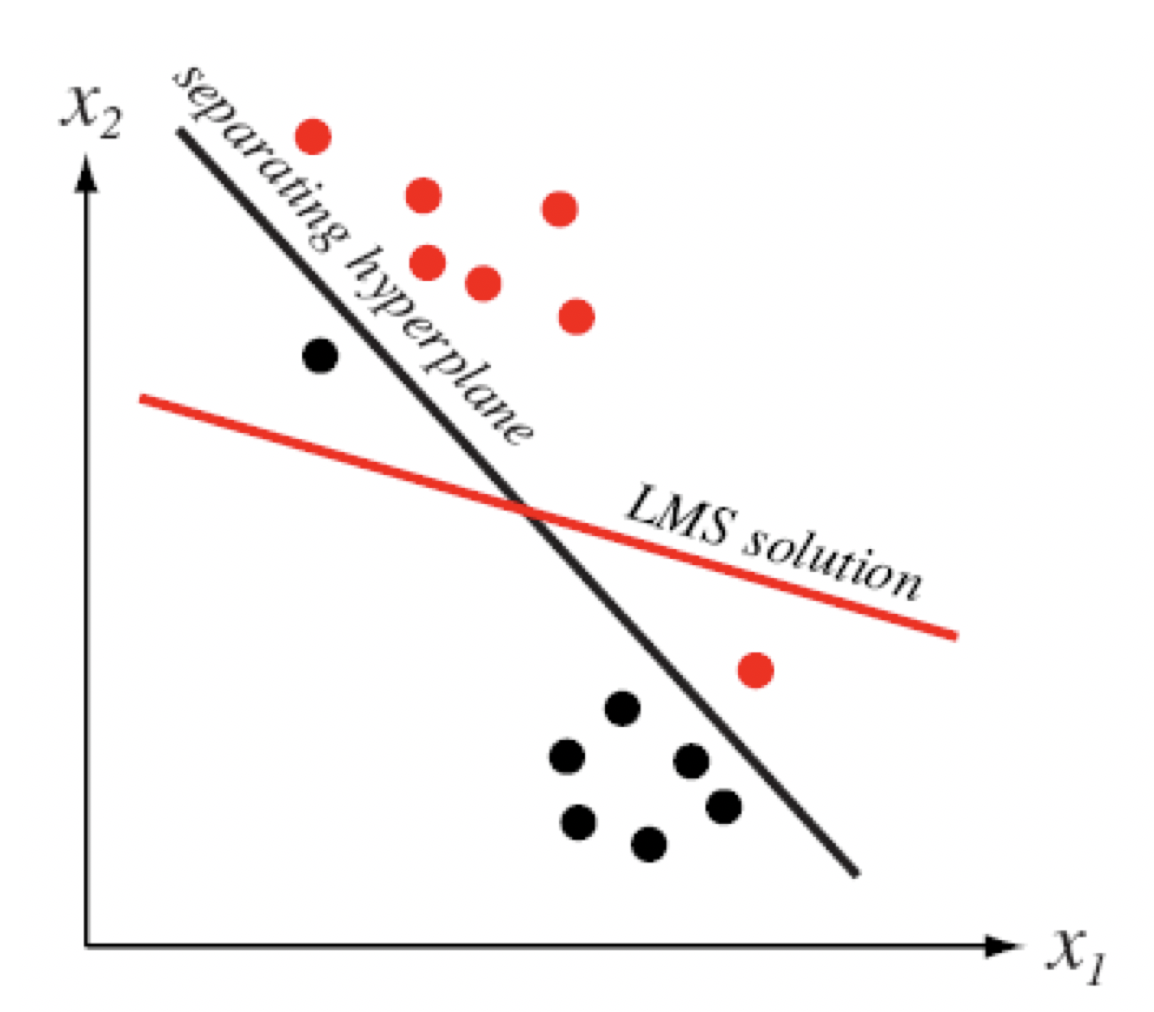
2.3 支持向量机SVM

这里是只是简单介绍SVM的基本概念，并解释其为什么是最优线性分类器，具体数学推导比较复杂，不做介绍。

• 首先思考这样一个问题，为什么要引入支持向量机，他与传统线性分类器之间的区别是什么？
  • 
  • 从这张图中，可以看见\(H_1\), \(H_2\)都是对于现有训练数据中的最优分类超平面。
  • 但是对于未来要预测的不存在与驯良样本集合中的数据，显然\(H_1\)的效果会更好。因为他距离各个类别的“距离最远”，鲁棒性肯定更强。而\(H_2\)离红色样本太近了，如果某一待预测红色样本的输入特征稍微“向左”偏移一点，\(H_2\)分类界面便认为其属于蓝色样本，分类错误。
  • SVM便是出于这种"距离最远"的想法，希望能够得到\(H_1\)类型的分类界面。

2.3.1 SVM数学概念

SVM采用几何间隔，来描述“距离”这一概念，而几何间隔的计算需要引入函数间隔。

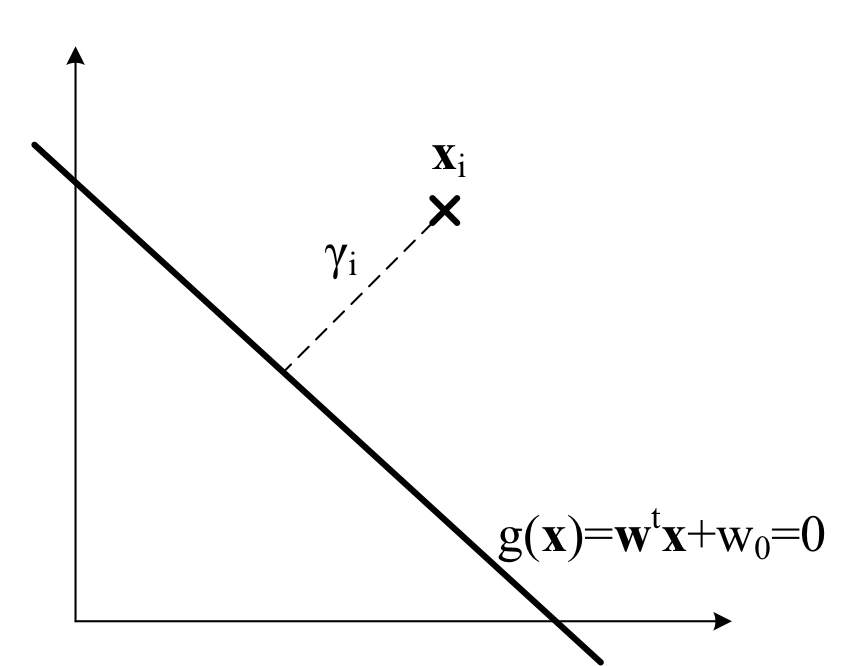
• 函数间隔：样本\(x_I\)到分类界面\(g(x)=0\)的函数间隔\(b_i\)，定义为：

\[b _ { i } = \left| g \left( \mathbf { x } _ { i } \right) \right| = \left| \mathbf { w } ^ { t } \mathbf { x } _ { i } + w _ { 0 } \right| \]

• 几何间隔；

\[\gamma _ { i } = \frac { b _ { i } } { \| \mathbf { w } \| } \]

• 如图所示：
  

2.3.2 为什么是最优线性分类器

• 样本集与分类界面之间的几何间隔$\gamma $定义为样本与分类界面之间几何间隔的最小值。
• 最优分类界面：给定线性可分样本集，能够将样本分开的最大间隔超平面。
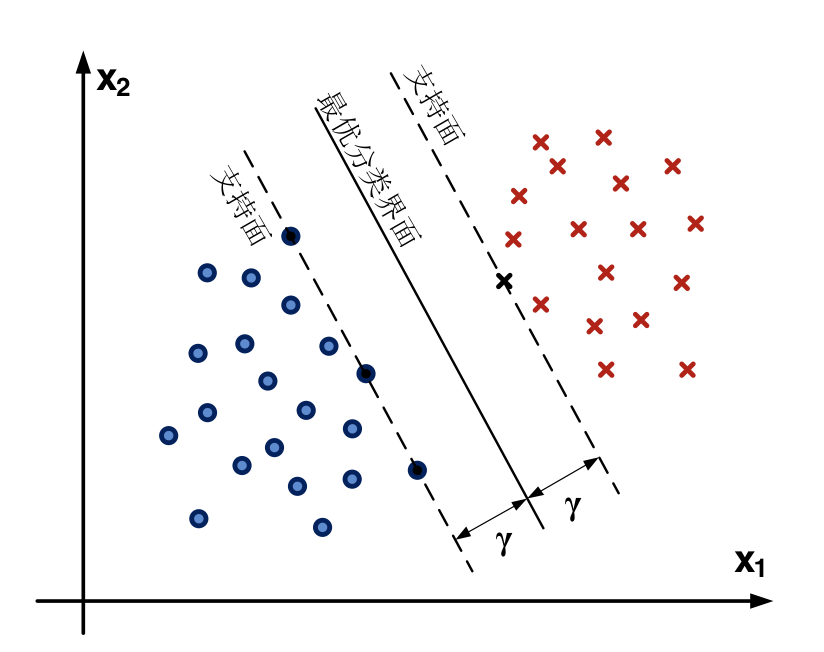
• SVM就是按照这种思想，希望得到与每个类别的支持矢量距离最大的分类平面。
  • 距离最优分类界面最近的这些训练样本称为支持矢量。
  • 最优分类界面完全由支持矢量决定，然而支持矢量的寻找比较困难。
• SVM作为最优线性分类器的介绍如图所示：
  

3. 多类问题

本章介绍如何将线性判别函数应用于多类问题。

3.1 处理方式

• 最常用的处理方式是one versus all的思想，每个类别与其他所有类别进行分类，在sklearn中用“ovr”表示，c类问题变为c个两类问题，需要c个线性分类界面。
  
  • 阴影为拒识区域，以下同理。
• 还有一种方式是one versus one的思想，分别对每两个类别进行分类，在sklearn中用“ovo”表示，c类问题变为\(c(c-1)/2\)个两类问题。
  
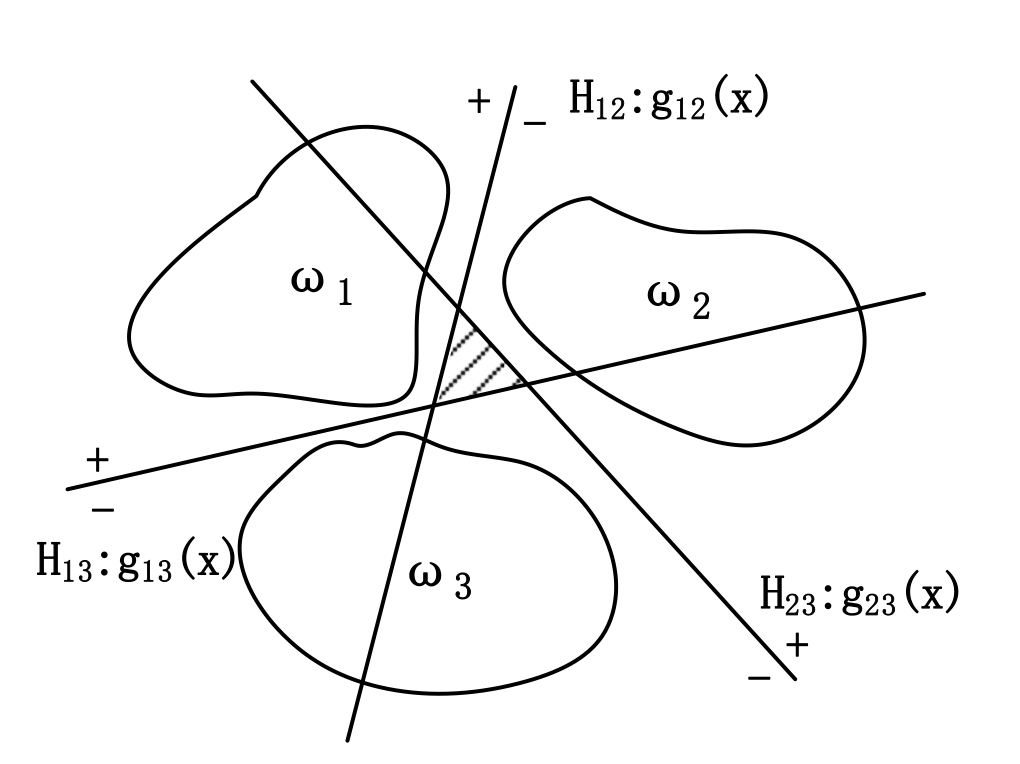
• 最后一种是采用票箱的方式，用c个线性判别函数处理c类问题，这种做法不存在拒识区域，在实际的数学推导过程中中，这c个票箱其实相当于\(c(c-1)/2\)个判别函数，因为是选择c个票箱中的最大值，也就是需要每个两个票箱进行相减计算，即c(c-1)/2$个判别函数，在排列组合中表示c个里取两个。
  • 对于感知器算法，可以用Kesler构造法进行设计，也可以称作扩展的感知器算法。