吴恩达深度学习笔记(deeplearning.ai)之循环神经网络(RNN)(一)
RNN
首先思考这样一个问题:在处理序列学习问题时,为什么不使用标准的神经网络(建立多个隐藏层得到最终的输出)解决,而是提出了RNN这一新概念?
标准神经网络如下图所示:
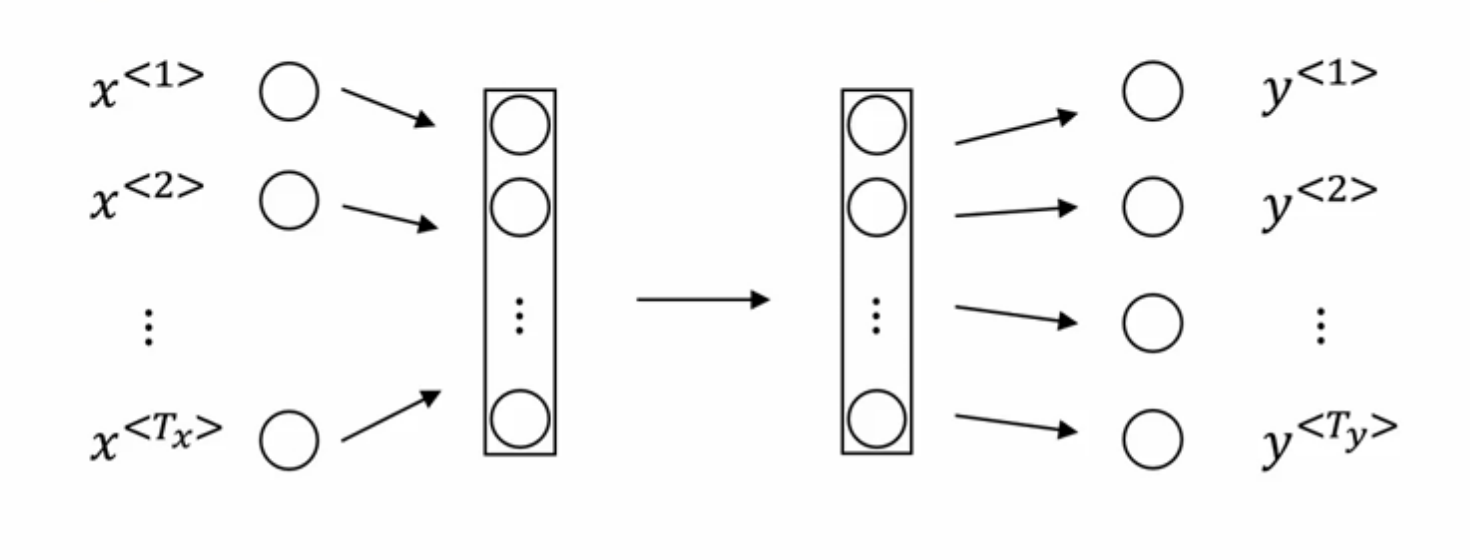
标准神经网络在解决序列问题时,存在两个问题:
- 难以解决每个训练样例子输入输出长度不同的情况,因为序列的长度代表着输入层、输出层的维度,不可能每训练一个样例就改变一次网络结构。
- 标准的神经网络不能共享从文本不同位置上学到的特征。举例说明:如果Harry作为人名位于一个训练例子中的第一个位置,而当Harry出现在其他例子的不同位置时,我们希望模型依然能识别其为人名,而不是只能识别位于第一个位置的Harry。
前向传播
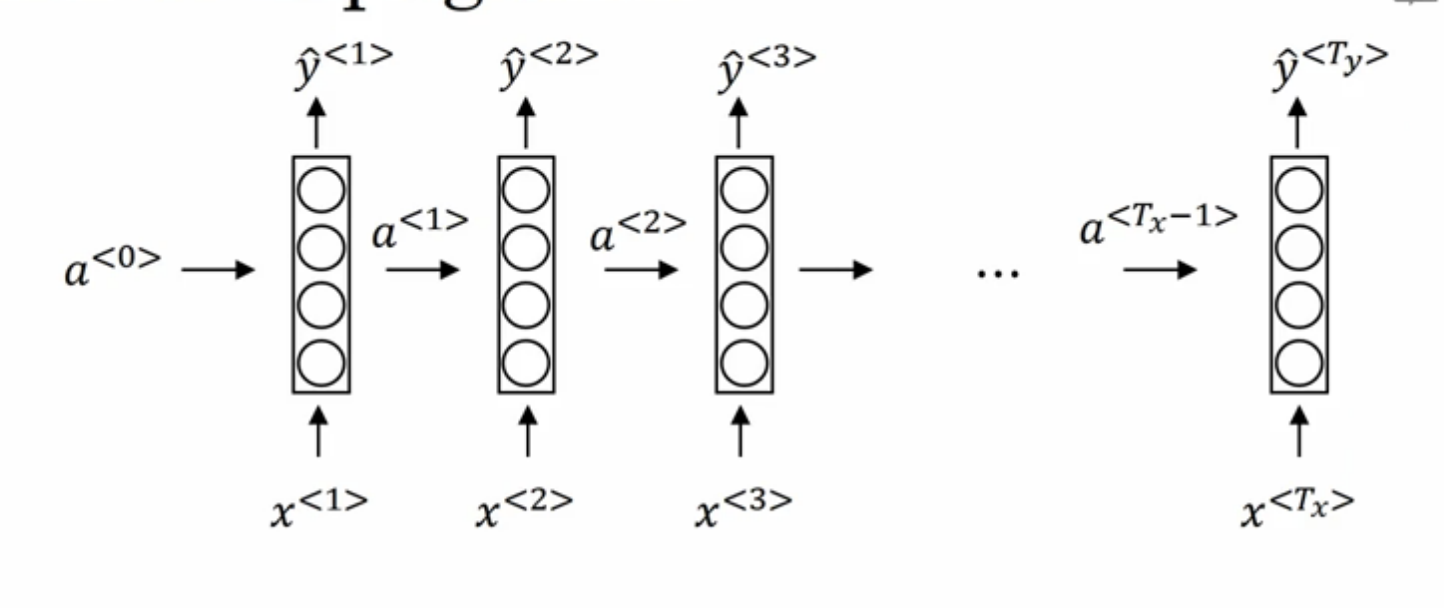
以NLP中“命名实体识别“任务为例,序列中每一个输入字符对应一个输出,即\(T_y=T_x\):
- \(a^{<0>}\)是初始的隐状态,一般置为零向量。
- \(a^{<i>}\)代表输入序列中第\(i\)个输入所隐含的信息,即时间步\(i\)的激活值。
- \(x^{<i>}\)代表输入序列中第i个字符,输入序列的长度为\(T_x\) 。
- \(\hat{y}^{<i>}\)代表与\(x^{<i>}\)相对应的输出值。
RNN在进行前向传播时,不光考虑当前时刻的输入\(x^{<i>}\),也会考虑包含上一时刻的信息(激活值\(a^{<i-1>}\))。计算公式如下:
\[a^{<t>}=g(W_{aa}a^{<t-1>}+W_{ax}x^{<t>}+b_a)
\]
\[\hat{y}^{<t>}=g(W_{ya}a^{<t>}+b_y)
\]
为了方便记忆,可以将公式进行简化,其中\(W_{aa}\), \(W_{ax}\)合并为\(W_a\),\(a^{<t-1>}\)与\(x^{<t>}\)合并为新的矩阵\([a^{<t-1>},x^{<t>}]\)。举例说明:假定激活值\(a^{<t-1>}\)(也可以成为隐状态)为\(100\)维,输入值\(x^{<t>}\)为\(10000\)维。那么权重矩阵\(W_{aa}\)为\(100\times 100\)维,\(W_{ax}\)为\(100\times 10000\)维。合并后的新权重矩阵为\(W_a\)为\(100\times (100+10000)\)维,合并后的新输入\([a^{<t-1>},x^{<t>}]\)为\((100+10000)\)维向量,即将\(a^{<t-1>}\)堆叠(stack)在\(x^{<t>}\)上方。
- 简化的原理为:
\[\begin{bmatrix}W_{aa}&W_{ax}\end{bmatrix}\begin{bmatrix}a^{<t-1>}\\ x^{<t>}\end{bmatrix}=W_{aa}a^{<t-1>}+W_{ax}x^{<t>}
\]
- 简化后的计算公式为:
\[a^{<t>}=g(W_{a}[a^{<t-1>},x^{<t>}]+b_a)
\]
\[\hat{y}^{<t>}=g(W_{y}a^{<t>}+b_y)
\]
RNN类型总结
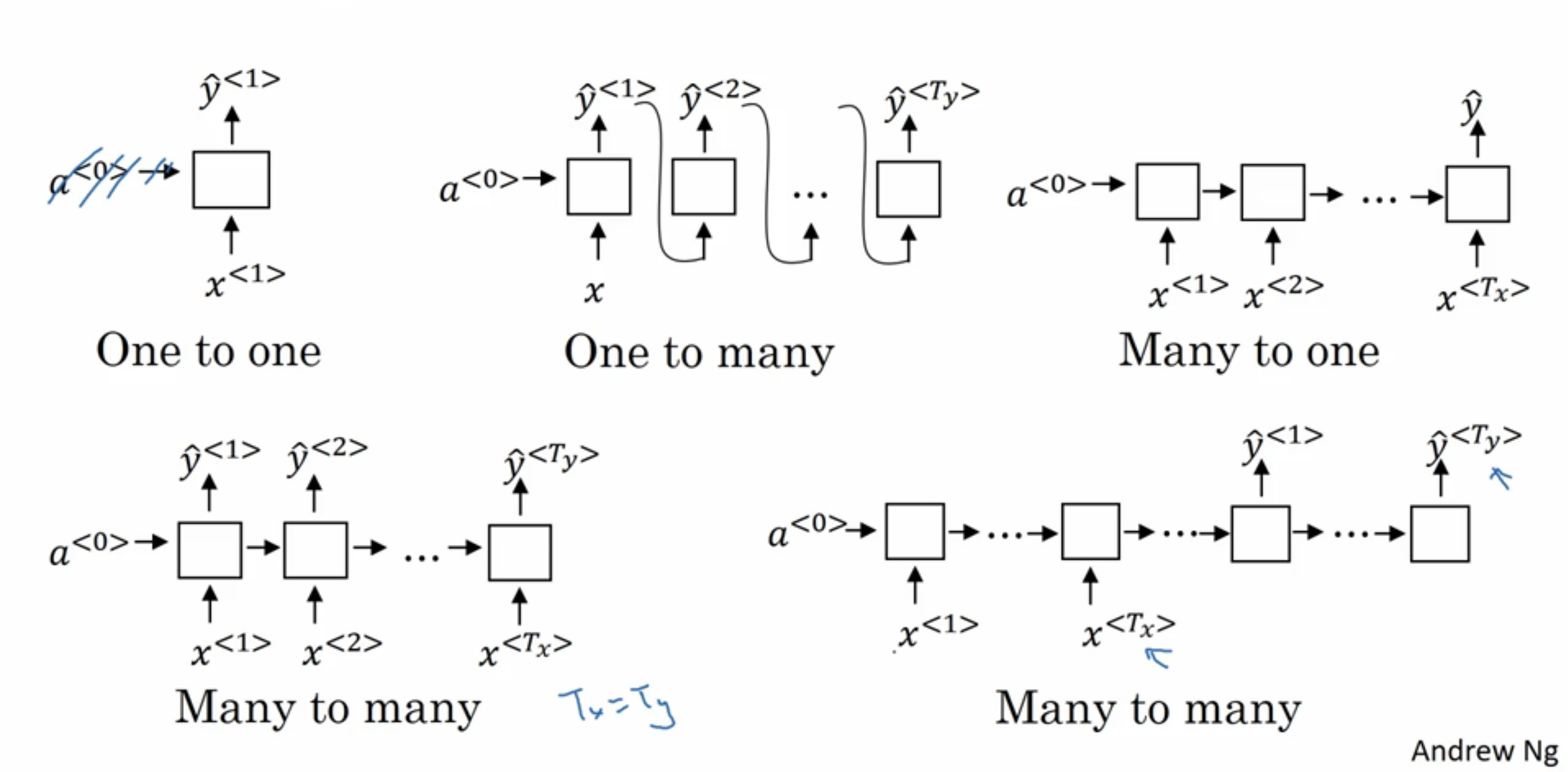
- One to one
- One to many
- Many to one
- Many to many(\(T_x == T_y\))
- Many to many(\(T_x != T_y\))




