Min-25筛

写一下如何抄对板子（原理还是有看的，大概是到了看得脑壳有点疼+似乎领略到了一些东西的程度，然后就可以心安理得地抄代码了）

step1:算g(n,j)

公式

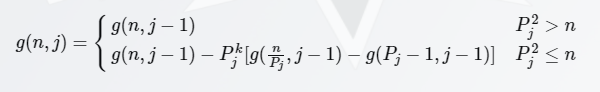
预处理

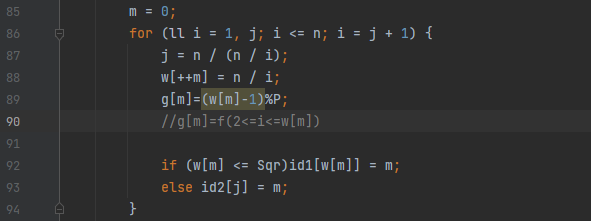
这里\(g\)的值是\(\sum_{i=2}^{n}f'(i)\)，其中\(f'(i)\)表示把\(i\)带入\(x\)为质数时\(f(x)\)的表达式，这里\(f(x)\)的表达式要求是完全积性的！（为了下一步筛出质数的\(f(x)\)之和的过程的正确性）

计算

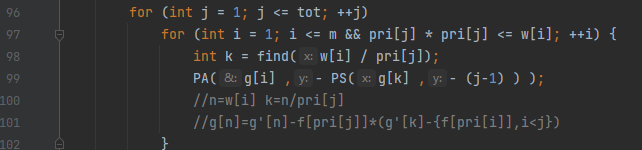
step2：算S(n,j)

公式

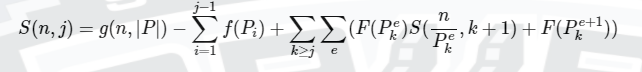
计算

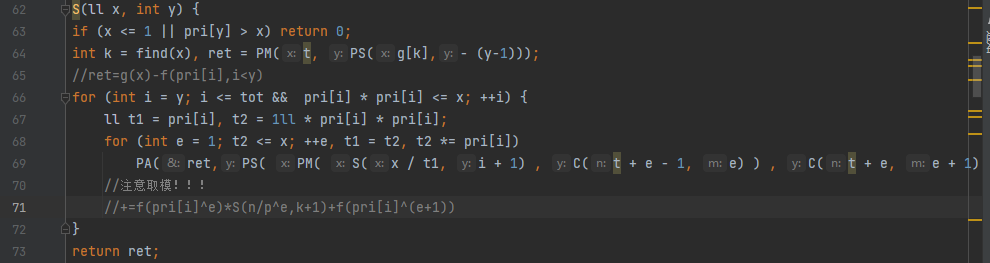
按照几处注释说的，把要算的式子代入即可。
取模较多，很容易寄，建议涉及取模的计算全部写成函数，就不容易错了！

整个板子

点击查看代码

namespace Min_25 {
    const int MAX=4e5+5,MOD=1e9+7;
    bool zs[MAX];
    int tot;
    ll pri[MAX];
    void pre(int n) {
        tot = 0;
        zs[1] = true; for (int i = 2; i <= n; ++i) zs[i]=0;
        for (int i = 2; i <= n; ++i) {
            if (!zs[i]) pri[++tot] = i;
            for (int j = 1; j <= tot && i * pri[j] <= n; ++j) {
                zs[i * pri[j]] = true;
                if (i % pri[j] == 0)break;
            }
        }
    }
    ll n, t, Sqr, w[MAX];
    int id1[MAX], id2[MAX], g[MAX], m;

    int find(ll x) {
        if (x <= Sqr) return id1[x];
        return id2[n / x];
    }

    int S(ll x, int y) {
        if (x <= 1 || pri[y] > x) return 0;
        int k = find(x), ret = PM(t, PS(g[k],- (y-1)));
        //ret=g(x)-f(pri[i],i<y)
        for (int i = y; i <= tot &&  pri[i] * pri[i] <= x; ++i) {
            ll t1 = pri[i], t2 = 1ll * pri[i] * pri[i];
            for (int e = 1; t2 <= x; ++e, t1 = t2, t2 *= pri[i])
                PA(ret,PS( PM( S(x / t1, i + 1) , C(t + e - 1, e) ) , C(t + e, e + 1) ));
            //注意取模！！！
            //+=f(pri[i]^e)*S(n/p^e,k+1)+f(pri[i]^(e+1))
        }
        return ret;
    }

    int work(int nn, int tt) {
        n = nn;
        t = tt;
        Sqr = sqrt(n);
        pre(Sqr);
        m = 0;
        for (ll i = 1, j; i <= n; i = j + 1) {
            j = n / (n / i);
            w[++m] = n / i;
            g[m]=(w[m]-1)%P;
            //g[m]=f(2<=i<=w[m])

            if (w[m] <= Sqr)id1[w[m]] = m;
            else id2[j] = m;
        }
        for (int j = 1; j <= tot; ++j)
            for (int i = 1; i <= m && pri[j] * pri[j] <= w[i]; ++i) {
                int k = find(w[i] / pri[j]);
                PA(g[i] ,- PS(g[k] ,- (j-1) ) );
                //n=w[i] k=n/pri[j]
                //g[n]=g'[n]-f[pri[j]]*(g'[k]-{f[pri[i]],i<j})
            }
        int ans = PS(S(n, 1) , 1);
        for (int i = 1; i <= Sqr; i++) id1[i] = id2[i] = 0;
        return ans;
    }
}

例题 HDU7217

题目链接
发现\(n\)固定的时候，要算前缀和的函数满足Min-25筛的要求，可以求出\(f(n)\)。
又发现上述\(f(n)\)是关于\(n\)的不超过\(Max(e_i),(e_i为唯一分解后的各个指数)\)次多项式，所以前缀和次数加一，取前32个分别算，再做一遍前缀和，然后插值即可。