马尔科夫链蒙特卡罗方法(MCMC)
一.蒙特卡罗法的缺陷
通常的蒙特卡罗方法可以模拟生成满足某个分布的随机向量,但是蒙特卡罗方法的缺陷就是难以对高维分布进行模拟。对于高维分布的模拟,最受欢迎的算法当属马尔科夫链蒙特卡罗算法(MCMC),他通过构造一条马尔科夫链来分步生成随机向量来逼近制定的分布,以达到减小运算量的目的。
二.马尔科夫链方法概要
马尔科夫链蒙特卡罗方法的基本思路就是想办法构造一个马尔科夫链,使得其平稳分布是给定的某分布,再逐步生模拟该马尔科夫链产生随机向量序列。其基本思路如下。就像是普通的蒙特卡罗方法本质上依赖于概率论中的大数定理,蒙特卡罗方法的理论支撑是具有遍历性的马尔科夫链的大数定理。马尔科夫链蒙特卡罗方法的大体思路如下:
(1)给定某个分布$p(x)$, 构造某个马尔科夫链$\lbrace X_{t}\rbrace_{t\in\mathbb{N}}$使得$p$是其平稳分布,且满足一定的特殊条件;
(2)从一点$x_{0}$出发,依照马尔科夫链$\lbrace X_{t}\rbrace_{t\in\mathbb{N}}$随机生成向量序列$x_{0},x_{1},...$;
(3)蒙特卡罗积分估计:计算$E_{p}(f)\approx\sum_{t=1}^{N}f(x_{t})$
三.MCMC的数学基础——马尔科夫链的遍历性,大数定理
MCMC为什么可以近似计算积分? 其实在数学上这是不太平凡的,下面简要介绍一下其数学理论依据。
3.1 马尔科夫链与其遍历性, 马尔科夫链的大数定理:
所谓马尔科夫链通俗的说就是一个随机过程,其满足,t时刻的状态和$t-1$之前的状态无关。我们用严格的测度论语言说就是:
定义3.1:定义于概率空间$(\Omega,\mathcal{G},P)$, 取值于$\mathcal{Y}\in\mathbb{R}^{K}$的随机向量序列$\lbrace X_{t}\rbrace_{t\in\mathbb{N}}$称为离散时间马尔科夫链(Markov Chain of discrete time)如果其满足:
对于任意$\mathcal{Y}$的Borel集$B\in \mathcal{B}_{\mathcal{Y}}$
$P(X_{t+1}^{-1}(B)\mid X_{t},...,X_{1})=P(X_{t+1}^{-1}(B)\mid X_{t})$
进一步的,如果$\lbrace X_{t}\rbrace_{t\in\mathbb{N}}$还满足:
\begin{equation}P(X_{t+1}^{-1}(B)\mid X_{t})=P(X_{1}^{-1}(B)\mid X_{0})\end{equation}
我们称马尔科夫链$\lbrace X_{t}\rbrace_{t\in\mathbb{N}}$为时间齐次(time homogeneous)的,这时我们定义该马尔科夫链的转移核(transition kernel)$$P_{t}: \mathbb{N}\times\mathcal{B}_{\mathcal{Y}}\longrightarrow [0,1]:$$
$$P_{t}(y,A)\triangleq P(X_{t}\in A\mid X_{0}=y),$$
对任意$t\in\mathbb{N}$, 并且我们直接简记$P(y,A)=P_{1}(y,A)$, 对$y\in\mathcal{Y}$, $A\in\mathcal{B}_{\mathcal{Y}}$。
为了方便起见,我们在这里的所有“马尔科夫链”均为离散时间,时间齐次的马尔科夫链。
如果这时候$\mathcal{Y}$上已经有一个定义于$\mathcal{Y}$上所有Borel集构成的$\sigma$代数$\mathcal{B}_{\mathcal{Y}}$上的$\sigma$有限测度$\nu$以及某个概率分布函数$p$, $\int_{\mathcal{Y}}pd\nu=1$, 则马尔科夫链$\lbrace X_{t}\rbrace_{t=1}^{\infty}$称为具有以$p$为平稳分布的遍历性(ergodicity),如果其满足:
1)非周期性(Aperiodicity):不存整数$T>1$以及互不相交的Borel集$B_{i}\in\mathcal{B}_{\mathcal{Y}}$, $i=1,...,T$使得:
对任意$y_{i}\in B_{i}$, $j\equiv i+1(\text{mod } T)$, 有:
\begin{equation}P(y_{i},B_{j})=1,\end{equation}
2)$p-$平稳性($p$-Invariance): 对任意的$A\in\mathcal{B}_{\mathcal{Y}}$
\begin{equation}\int_{\mathcal{Y}}P(y,A)p(y)d\nu(y)=\int_{\mathcal{Y}}p(y)d\nu(y)\end{equation}
3)$p-$不可约性($p$-Irreducibility):
对任意的$y\in\mathcal{Y}$, $A\in\mathcal{B}_{\mathcal{Y}}$, $\int_{A}p d\nu>0$, 存在$t\in\mathbb{N}$使得
\begin{equation}P_{t}(y,A)>0\end{equation}
4)Harris 回归性(Harris Recurrence): 对任意$A\in\mathcal{B}_{\mathcal{Y}}$, $\int_{A}p(y)d\nu(y)>0$, 马尔科夫链$X$以概率为1,无数次经过$A$:
\begin{equation}P(\sum_{t=1}^{\infty}\text{I}_{\lbrace X_{t}\in A\rbrace}=+\infty\mid X_{0}=y)=1\end{equation}
3.2 马尔科夫链的大数定理
我们知道,经典的大数定理要求是随机序列$\lbrace X_{t}\rbrace_{t\in\mathbb{N}}$满足独立同分布假设。但是问题来了,对于马尔科夫链,自然独立同分布假设一般是不满足的,那么凭什么大数定理成立,也就是我们可以生成马尔科夫链的样本来近似计算积分? 下面的马尔科夫链的大数定理(large number theorem of markov chains)是MCMC算法的数学基础,回答了以上问题:
定理3.1(马尔科夫链的大数定理):如果马尔科夫链$\lbrace X_{t}\rbrace$具有以概率分布函数$p$为平稳分布的遍历性,$g\in L^{1}_{pd\nu}(\mathcal{Y})$,那么我们有几乎处处收敛:
\begin{equation}\frac{1}{m}\sum_{t=1}^{m}g(X_{t})\longrightarrow\int_{\mathcal{Y}}g(y)p(y)d\nu,\end{equation}
并且:
\begin{equation}P_{t}(y, A)\longrightarrow \int_{A}pd\nu\end{equation}
对于p-几乎处处的$y\in\mathcal{Y}$.
马尔科夫链的大数定理是概率论中极其深刻而优雅的定理,其证明相当复杂,完整的证明也许得写本小书专门讲,参见[3]的定理4.3。
马尔科夫链的大数定理告诉我们以下的事实:
如果马尔科夫链有以$p$为平稳分布的遍历性,则对几乎处处(几乎所有)的$y$, 从$y$状态出发,$X_{t}$渐进趋于均衡分布$p$,这是非常有趣的性质,那就是渐进状态和初始值无关,这也自然的提供我们模拟生成服从$p$分布随机数的思路。另外,(6)保证了估算积分值的合法性。
四. Metropolis Hastings 算法:
现在我们考虑如何实现一个MCMC算法。现在我们给定了某个概率分布函数$p$,其实整个算法实施的关键仅仅在于如何构造一个具有以$p$为平稳分布遍历性的马尔科夫链,下面的Metropolis-Hastings算法给出一种方法。
Metropolis-Hatings算法的历史很耐人寻味,最初由物理学家在第二次世界大战期间于洛斯阿拉莫斯实验室研制原子弹时发现,于1953年首次提出于由Nicholas Metropolis, Arianna W. Rosenbluth, Marshall Rosenbluth, Augusta H. Teller, Edward Teller五人署名,短短四页的一篇发表于某化学杂志的文章里[6],他们在这篇文章里模拟了Boltzmann分布的采样,一个推广工作,也是现今更加广泛采用的版本是由W.Hatings于1970年给出[7],一个特殊的版本于1984年在S.Geman, D.Geman于伊辛模型的研究中独立提出,现在被称为Gibbs采样算法[8]。但是这类算法并没有得到统计学界的足够关注,一直到1990年Gelfand, Smith的工作[9]。该算法名声大噪之后,最初的五位提出者陷入旷日持久的名誉争夺战,因为其他人对该算法仅仅命名Metropolis-Hastings算法感到不满。
我们在这里沿用之前的记号和约定。这时如果存在可测函数$p(\cdot,\cdot):\mathcal{Y}\times\mathcal{Y}\longrightarrow \mathbb{R}^{+}$, 使得马尔科夫链$\lbrace X_{t}\rbrace_{t\in\mathbb{N}}$的转移核满足:
\begin{equation}P(y, A)=\int_{A}p(y,z)d\nu(z),\end{equation}
对任意$(y, A)\in\mathcal{Y}\times\mathcal{B}_{\mathcal{Y}}$,则称该函数为马尔科夫链$\lbrace X_{t}\rbrace$的转移分布函数(triansition distribution function)。
Metropolis Hastings算法的具体思路是模拟一个转移分布函数$p:\mathcal{Y}\times\mathcal{Y}\longrightarrow \mathbb{R}$满足:
\begin{equation}p(y)p(y,z)=p(z)p(z,y)\end{equation}
的马尔科夫链,以上条件称作细致平衡(detailed balance)。我们知道,如果细致平衡条件满足,则对任意的$A\in\mathcal{B}_{\mathcal{Y}}$两边取积分$\int_{\lbrace (y,z)\in\mathcal{Y}\times A\rbrace} d\nu(y)\times d\nu(z)$我们得到:
\begin{equation}\int_{\lbrace (y,z)\in\mathcal{Y}\times A\rbrace} p(y)p(y,z)d\nu(y)\times d\nu(z)=\int_{\lbrace (y,z)\in \mathcal{Y}\times A\rbrace}p(y)p(y,z)d\nu(y)\times d\nu(z),\end{equation}
由Fubini定理容易计算上式左边为$\int_{A}p(y)P(y,A)d\nu(y)$, 右边为$\int_{A}p d\nu$, 所以:
\begin{equation}\int_{A}p d\nu=\int_{A}p(y)P(y,A)d\nu(y),\end{equation}
所以这时相应的以$p(\cdot,\cdot)$为转移分布函数的马尔科夫链必然是$p-$不变的,也就是说细致平衡条件是比$p$-不变性更加强的限制条件。(物理意义是什么?以后慢慢了解。)
现在的问题是我们如何构造这样的一个$p(\cdot,\cdot)$?下面我们探讨一下。我们先做一个如下的模拟实验:
和常见的蒙特卡罗方法一样,假如我们已经有一个提议分布(proposal distribution) $q(y, z)$, 是一个常见的,容易进行模拟的分布,那么这时候由状态$y$出发下一步模拟以分布$q(y, \cdot)$生成一个向量$z$, 一般来说$z\neq y$, 这时如果我们继续做模拟,也就是模拟$z$ 以某概率(待定)$\alpha(y, z)$ 生成 $z$,而以概率$1-\alpha(y, z)$生成$y$,
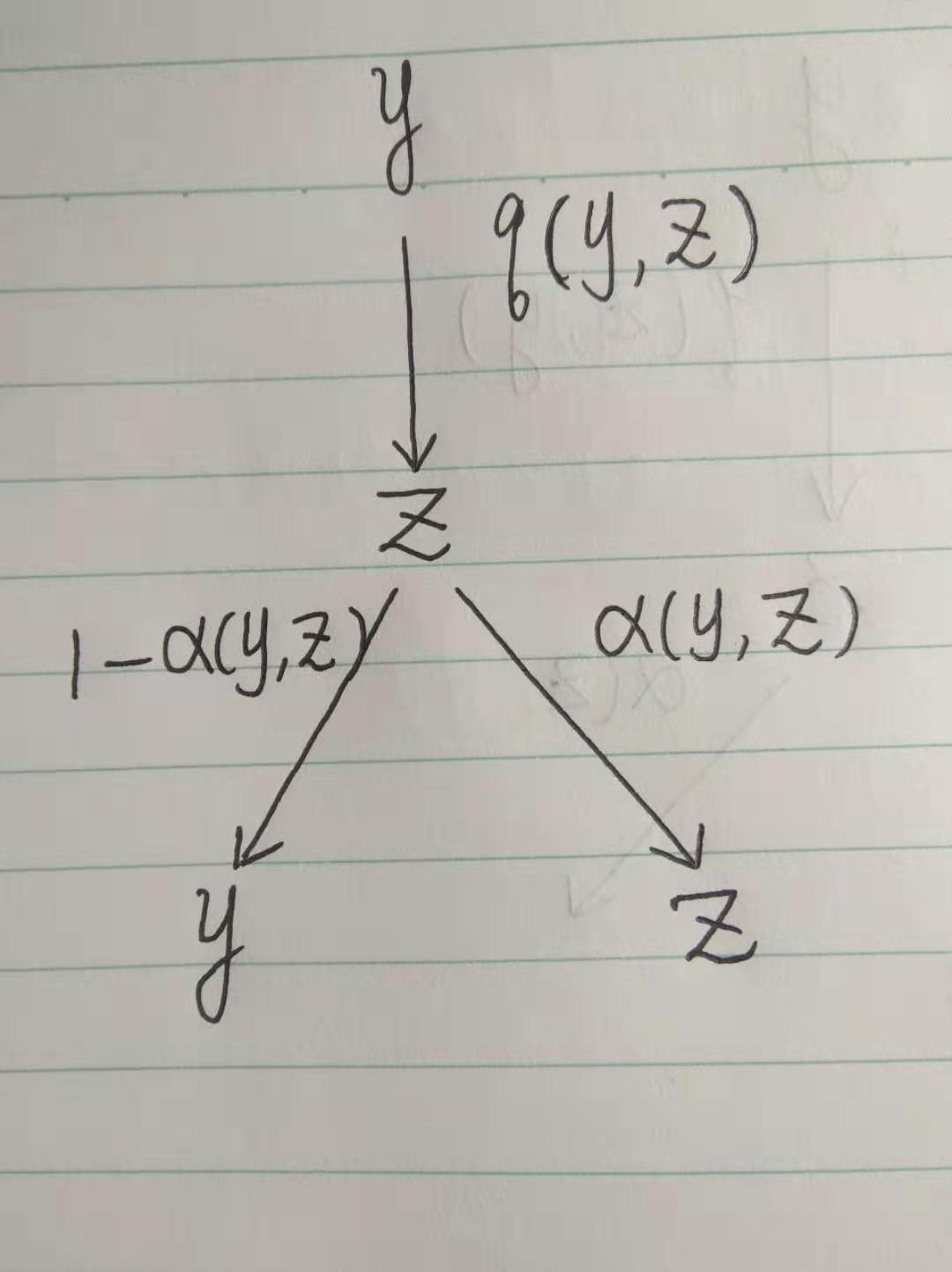
现在我们来看一下,这样模拟后得到的转移分布函数:
\[p(y,z)=\begin{cases}q(y,z)\alpha(y,z)&\text{if } z\neq y,\\g(y)&\text{if }z=y,\end{cases}\]
其中$q(y)$是某个关于$y$的函数使得$\int_{\mathcal{Y}}p(y,z)d\nu(z)=1$, 例如我们可以取$q(y)=(1-\int_{\mathcal{\lbrace z\mid z\in\mathcal{Y},z\neq y\rbrace}}q(y,z)\alpha(y,z)d\nu(z) )/\nu(\lbrace y\rbrace)$, 当$\nu(\lbrace y\rbrace)>0$, 而直接取$0$当$\nu(\lbrace y\rbrace)=0.$
这时候我们要求$p(\cdot,\cdot)$满足细致平衡条件,也就是要求:
\begin{equation}p(y)q(y,z)\alpha(y,z)=p(z)q(z,y)\alpha(z,y)\end{equation}
由上面的公式,我们知道,如果能够找到某个对称函数$\lambda(y,z)$使得:
$$\alpha(y,z)=\lambda(y,z)p(z)q(z,y),$$
则(12)自动满足。而想其成为概率值,必然有$\lambda(y,z)\leq \frac{1}{p(z)q(z,y)}$, 再由对称性$\lambda(y,z)=\lambda(z,y)\leq \frac{1}{p(y)p(y,z)}$, 于是乎我们只需要取$\lambda(y,z)=\min\lbrace \frac{1}{p(z)q(z,y)}, \frac{1}{p(y)p(y,z)}\rbrace,$
这时候自然有:
\begin{equation}\alpha(y,z)=\min\lbrace \frac{p(z)q(z,y)}{p(y)q(y,z)},1\rbrace\end{equation}
所以依照以上方法,我们确实可以得到某个$p(\cdot,\cdot)$满足细致平衡条件,然后我们就可以模拟产生以此为转移分布函数的马尔科夫链的样本。
我们总结Metropolis Hasting算法如下:
算法4.1(Metropolis Hasting):
任意选择某个$x_{0}$, 我们假设现在已经生成了$x_{0},...,x_{t}$, $t\in\mathbb{N}$, 现在我们迭代生成$x_{t+1}$, 以如下方式:
(1)按照提议分布$q(x_{t},\cdot)$生成某数$y_{t}$
(2)计算出:
\begin{equation}\alpha(x_{t},y_{t})=\min\lbrace \frac{p(y_{t})q(y_{t},x_{t})}{p(x_{t})q(x_{t},y_{t})},1\rbrace\end{equation}
(3)随机生成某数$u\sim U([0,1])$,如果$u\leq \alpha(x_{t},y_{t})$,令$x_{t+1}=y_{t}$,否则令$x_{t+1}=x_{t}$.
以上是Metropolis Hastings算法的直观推导,但是问题来了,这时候构造的马尔科夫链是不是真的是遍历的? 如果是的话我们才可以用该算法估算积分值。幸运的是,可以证明该种算法能确保相应马尔科夫链的遍历性:
定理4.1:如果马尔科夫链$\lbrace X_{t}\rbrace_{t\in\mathbb{N}}$的转移分布函数$p(\cdot,\cdot)$为上述Metropolis-Hastings算法中的方法构造的函数, 则该马尔科夫具有遍历性。
定理的证明在这里不赘述,具体来说在[5]中2.4节可以找到非周期性的证明,而在[4]中可以找到Harris回归性的证明。
五.参考文献
[1]Jun Shao, Mathematical Statistics, second edition, Springer Texts in Statistics, 2003 Springer Science+Business Media, LLC.
[2]Larry Wasserman, All of Statistics: A Concise Course in Statistical Inference,
[3]D. Revuz, Markov Chains, North-Holland Mathematical Library. Vol 11, 1984, North-Holland, Amsterdam, New York, Oxford.
[4]Luke Tierney, Markov Chains for Exploring Posterior Distributions, The Annals of Statistics, Vol. 22, No. 4. (Dec., 1994), pp. 1701-1728.
[5]E.Nummelin, General Irreducible Markov Chains and non-negative operators, Cambridge Tracks in Mathematics, Cambridge University Press,1984.
[6]N.Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller, and E. Teller (1953). Equation of state calculations by fast computing machines. J. of Chemical Physics 21, 1087–1092.
[7]W.Hastings,(1970). Monte carlo sampling methods using markov chains and their applications. Biometrika 57(1), 97–109.
[8]S.Geman. and D. Geman (1984). Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. on Pattern Analysis and Machine Intelligence 6(6).
[9]A.Gelfand, and A. Smith (1990). Sampling-based approaches to calculating marginal densities. J. of the Am. Stat. Assoc. 85, 385–409.
[10]Kevin P. Murphy, Machine Learning A Probabilistic Perspective,2012 Massachusetts Institute of Technology


