蒙特卡罗方法

   

     所谓蒙特卡罗方法（Monte Carlo method），也称为统计模拟方法，指的是一系列随机模拟某个分布，然后近似计算某些量的方法。蒙特卡罗方法在金融，计算物理，机器学习等领域有着广泛的应用。蒙特卡罗方法的命名来自于大数学家冯诺依曼(John von Neumann)，其将该算法命名为一家摩纳哥的世界著名赌场的名字，给该算法增加了一层神秘色彩。

 

1. 逆概率变换法（inverse probability transform）。

 

     蒙特卡罗方法的核心问题其实是给定一个分，如何按照该分布模拟生成随机数(向量)，我们先来看一个最简单情况。已知一个取值非负的函数（实际问题中一般是连续函数）$p:\mathbb{R}\longrightarrow\mathbb{R}^{+}$，如果其满足$\int_{-\infty}^{+\infty}p(x)dx=1$，那么如何模拟生成随机数$X$使得$X\sim p$?

     一种最简单的办法是直接利用分布函数（Cumulative Distribution Function, 简称CDF）F的反函数，这种方法称为逆概率变换法（inverse probability transform）。

     首先，计算机可以利用线性同余发生器（Linear congruential generator）生成伪随机数, 来模拟均匀分布$U([0,1])$。下面我们看下面的一个简单结论：

     命题1.1. 如果$F$是某个概率分布的分布函数，其反函数$F^{-1}$存在，如果随机变量$U\sim U([0,1])$，则$F^{-1}(U)\sim F$。

     以上结论从下面等式立马可以被观察到，当$U\sim U([0,1])$的时候，对于任意$c\in\mathbb{R}$：

                        \begin{equation}P(F^{-1}(U)\leq c)=P(U\leq F(c))=F(c),\end{equation}

所以我们只要知道了某个分布函数的反函数，则模拟该分布生成随机数就很容易了，所幸的是常见的分布族求解反函数都还比较容易。

 

2. Box-Muller变换生成模拟正态分布

    

    我们现在想模拟二维标准正态分布，其概率密度是$p(x,y)=\frac{1}{2\pi}e^{-\frac{x^{2}+y^{2}}{2}}$，对任意的$(x,y)\in\mathbb{R}^{2}$。除了上面的逆概率变换法外还有一种更加方便的算法。

    我们用极坐标表示$\mathbb{R}^{2}$中的点：$x=r\cos\theta$,$y=r\sin\theta$, $r\in[0,\infty)$, $\theta\in[0,2\pi)$, 概率计算的时候的积分项（测度）在极坐标下有：

    \begin{equation}\begin{split}&\frac{1}{2\pi}e^{-\frac{x^{2}+y^{2}}{2}}\text{d}x\cdot\text{d}y\newline =&\frac{1}{2\pi}e^{-\frac{r^{2}}{2}}r\text{d}r\cdot\text{d}\theta\newline =&e^{-\frac{r^{2}}{2}}r\text{d}r\cdot\text{d}(\frac{\theta}{2\pi})\newline =&\text{d}(e^{-\frac{r^{2}}{2}})\cdot\text{d}(\frac{\theta}{2\pi})\end{split},\end{equation}

所以我们做一个变量替换:\begin{equation}\begin{split}u=&e^{-\frac{r^{2}}{2}}\newline v=&\frac{\theta}{2\pi},\end{split}\end{equation}

或者等价于: \begin{equation}\begin{split}x=&\sqrt{-2\log(u)}\cos(2\pi v)\newline y=&\sqrt{-2\log(u)}\sin(2\pi v)\end{split}\end{equation}  

的时候，我们必然有：\begin{equation}\text{d}u\cdot\text{d}v=\frac{1}{2\pi}e^{-\frac{x^{2}+y^{2}}{2}}\text{d}x\cdot\text{d}y.\end{equation}

   由上面的式子我们立即知道，如果定义一个变换：

                                             $$BM: [0,1]\times [0,1]\longrightarrow \mathbb{R}^{2},$$

                                                  \begin{equation}BM(u,v)\triangleq (\sqrt{-2\log(u)}\cos(2\pi v), \sqrt{-2\log(u)}\sin(2\pi v)),\end{equation}

则对于任意独立的$U_{1}\sim U([0,1])$， $U_{2}\sim U([0,1])$，$(V_{1}, V_{2})\triangleq BM(U_{1}, U_{2})\sim \mathcal{N}(0,\text{I}).$

 

 

3.拒绝-接受算法：

 

      3.1. 拒绝-接受算法的推导

 

        拒绝-接受算法的大体思路是先模拟某个比较容易模拟的提议分布(proposal probability)生成随机数（向量），然后用一定的概率来二次把关，决定是保留还是不要该数（向量），以达到保留该数（向量）的条件下该数（向量）的分布为预期要模拟的分布。

        具体来说是这样：

        假设给定了某个待模拟的$K$维分布的概率密度函数$p$,  现在选择一个容易模拟的分布，其概率密度$q$，生成一个随机数$X$，然后生成一个$Y\sim U([0,1])$, 两过程完全独立，我们想设定一个接受$X$之概率$r(X)$，也就是当$Y\leq r(X)$的时候才接受$X$，否则拒绝。

        这个时候我们定义事件：\begin{equation}A=\lbrace Y\leq r(X)\rbrace,\end{equation}

该事件就是"采样被接受"。我们希望$X$在$A$上的条件概率密度为$p$。也就是希望：

                                 \begin{equation}P(X\leq c\mid A)=\int_{-\infty}^{c}p(x)\text{d}x,\end{equation}

对于任意的$c\in\mathbb{R}^{K}$，其中$\text{''}\leq\text{''}$表示每个分量都不大于。

        我们容易计算：

                                \begin{equation}\begin{split}P(X\leq c\mid A)=&P(\lbrace X\leq c,Y\leq r(X)\rbrace)/P(\lbrace Y\leq r(X)\rbrace)\newline =&\int_{\lbrace (x,y)\mid x\leq c,y\leq r(x)\rbrace}Mq(x)\text{d}x\text{d}y \newline =&\int_{-\infty}^{c}M q(x)(\int_{0}^{r(x)}\text{d}y)\text{d}x\newline =&\int_{-\infty}^{c}Mq(x)r(x)\text{d}x,\end{split}\end{equation}

其中$M=(\int_{\mathbb{R}^{K}}q(x)r(x)\text{d}x)^{-1}$, 所以我们有：

                              $$p(x)=M q(x)r(x),$$

所以我们立即得到：\begin{equation}r(x)=\frac{p(x)}{M q(x)},\end{equation}     

别忘记了$r(x)\in [0,1],$所以$M$还得足够大使得：$Mq(x)\geq p(x)$。    

       综上所述我们总结一下接受-拒绝采样得到一个向量的方法：    

---

      算法(接受-拒绝采样)：

             1)选择一个合适的，容易模拟的具有概率密度$q(x)$的提议分布，选择一个足够大的$M$使得$Mq(x)\geq p(x)$；

             2)模拟提议分布，生成$z$；

             3)从均匀分布$U([0,1])$抽样得到$u$；

             4)如果$u\leq \frac{p(x)}{Mq(x)}$，令$x_{0}=z$，否则回到步骤1)继续，直到得到一个被接受的向量。

---

 

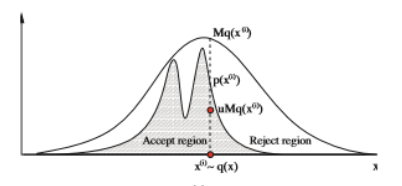
     3.2. 拒绝-接受采样的缺陷：

     拒绝接受采样的缺陷很明显，那就是当$M$过大的时候，算法的效率极其低下。因为每次试验生成的随机数或者向量被接受的概率仅仅为$\frac{1}{M}$，所以我们必须平均生成$M$个数(向量)才能最终成功采样其中一个。当我们采样的维度$K$非常大的时候(例如在统计物理中的模拟问题)，往往首先$q$难以寻找，齐次就算找到$M$相应也会很大，显然拒绝-接受采样不合适，所以一般它只适用于低维分布。

 

4.重要性采样

   

      现在假设某$K$维随机变量$X$有概率密度$p$，我们现在考虑用一种蒙特卡罗方法计算期望，也就是右边的积分：

    \begin{equation}E(f(X))=\int_{\mathbb{R}^{K}}f(x)p(x)\text{d}x.\end{equation}

      现在如果选取一个提议分布，密度函数为$q$，则对于任意的$\tilde X\sim q,$

    \begin{equation}\begin{split}E(f(X))=&\int_{\mathbb{R}^{K}}f(x)p(x)\text{d}x\newline =&\int_{\mathbb{R}^{K}}\frac{f(x)p(x)}{q(x)}q(x)\text{d}x\newline =&E(\frac{f(\tilde X)p(\tilde X)}{q(\tilde X)})\newline =&E(f(\tilde X)w(\tilde X)),\end{split}\end{equation}

在这里我们定义函数$w\triangleq \frac{p}{q}.$ 

      称$w(X_{i})$为$X_{i}$的重要性权重(importance weights)。令$I=\sum_{i=1}^{N}f(X_{i})w(X_{i})$，由大数定理，$I$几乎处处收敛于$E(f(X_{1})w(X_{1}))=E(f(X))$，所以我们可以取足够大的$N$, 这时就可以近似计算得到：$E(f)\approx I.$。我们总结一下该算法（重要性采样，Importance Sampling）：

 

---

      重要性采样：

              1)选择某个容易模拟的提议分布，具有概率密度$q$，然后模拟该分布生成$x_{1},...,x_{N}$；

              2)计算$I=\sum_{i=1}^{N}f(x_{i})p(x_{i})/q(x_{i})$，得到近似估计值$E(f)\approx I$。     

---

                          

      现在我们来考察一下方差\begin{equation}\delta_{q}^{2}=Var(f(\tilde X)w(\tilde X))\end{equation}，因为他直接影响着$I\longrightarrow E(f(X))$的收敛速率。由中心极限定理，当$N$足够大的时候$\frac{I-E(f)}{\delta_{q}/\sqrt{N}}$近似服从标准正态分布$\mathcal{N}(0,\text{I})$，由此我们可以近似给出$E(f(X))$的一个近似$1-\alpha$置信区间：

      \begin{equation}(I-\frac{\delta_{q}}{\sqrt{N}}z_{\alpha/2},I+\frac{\delta_{q}}{\sqrt{N}}z_{\alpha/2}),\end{equation} 

而$Var(f(\tilde X)w(\tilde X))=E(f^{2}(\tilde X)w^{2}(\tilde X))-E(f(\tilde X))^{2}$，于是我们只需要估计一下$E(f^{2}(\tilde X)w^{2}(\tilde X)).$由Cauchy-Schwarz不等式：

              \begin{equation}E(f^{2}(\tilde X)w^{2}(\tilde X))\geq (E(f(\tilde X)w(\tilde X)))^{2}=E(f(X))^{2},\end{equation}

等号成立当且仅当：$\vert fw\vert\equiv \text{const}$，也就是：\begin{equation}q(x)=q^{\ast}(x)\triangleq\frac{\vert f(x)\vert p(x)}{\int_{\mathbb{R}^{K}}\vert f(u)\vert p(u)\text{d}u}\end{equation}

的时候$E(f^{2}(\tilde X)w^{2}(\tilde X))$取极小值$E(f(X))^{2}$，此时$\delta_{q}^{2}$取最小值$Var(f(X))$。所以为了保证我们能用更小的生成向量个数$N$以得到足够小的置信区间，我们理想状态是选择某个提议分布使得其概率密度$q(x)$接近于$\frac{\vert f(x)\vert p(x)}{\int_{\mathbb{R}^{K}}\vert f(u)\vert p(u)\text{d}u}$。但是往往这是很难办到的，尤其是分布的维数$K$很大的时候，该算法收敛可能还是会出现比较慢的问题。

      下面我们看一个例子，看看提议分布的选取如何影响收敛速度，该例子取自于[1]的例25.6。

    

 

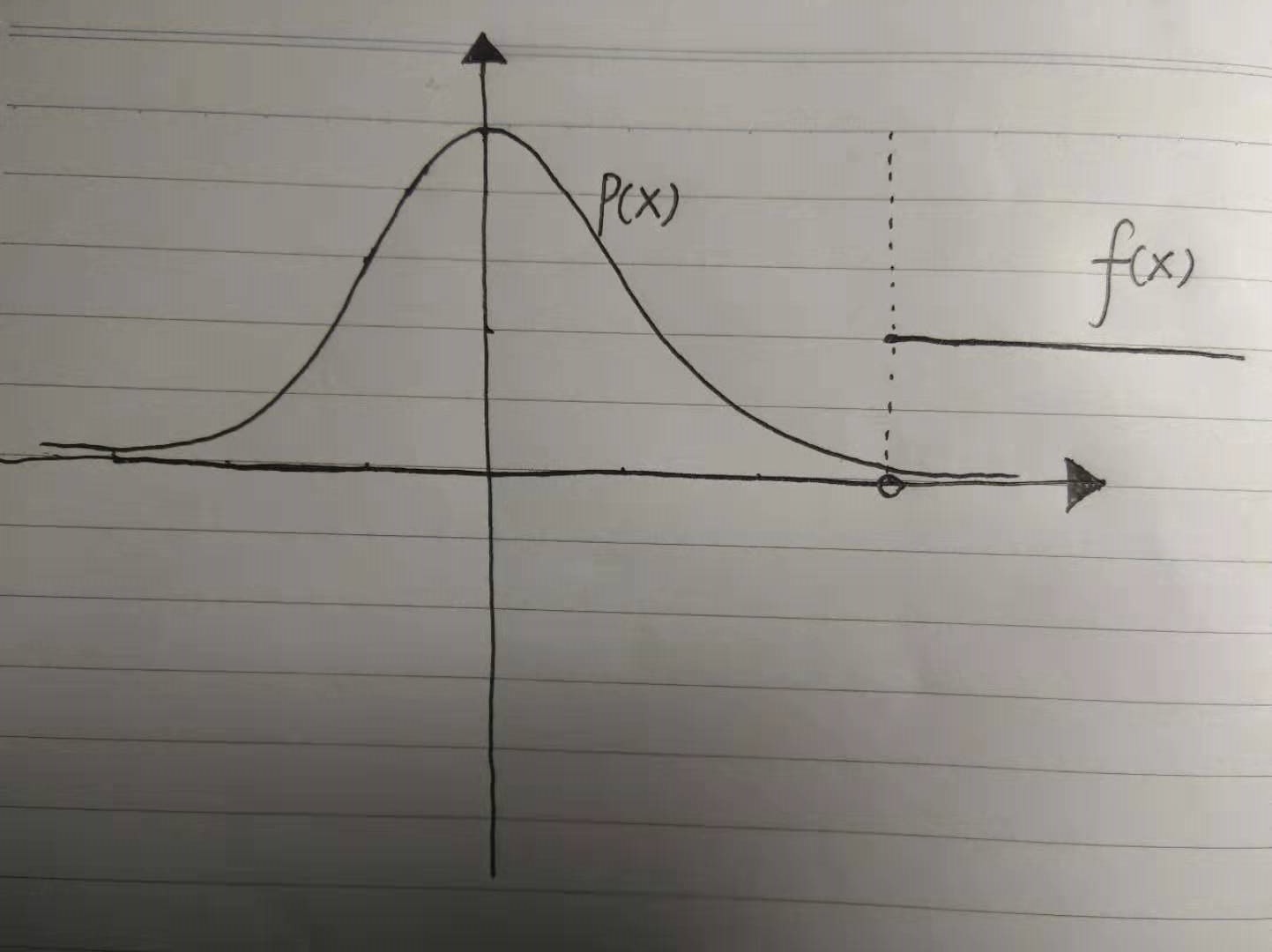
      例4.1  如上图，我们令概率密度$p(x)=(2\pi)^{-\frac{1}{2}}e^{-\frac{x^{2}}{2}}$，表示标准正态分布的概率密度函数，$f(x)=100$如果$x\geq 3$, 否则$f(x)=0$。这时候如果我们先直接取$q=p$，生成随机数$X_{i}\sim p$，$i=1,...,N$，$N=100$来近似计算$E(f(X))= 10P(X > 3) =0.0013$，看看会发生什么。首先，如果$N$取得太小，例如是这里的100,那么我们抽样得到右边尾部$[3,\infty)$的概率极其低，几乎抽不到这里的点，算出来的$I$大概率是$0$。我们再计算一下得到$Var(I)=0.039$。这时这种抽样效率显然过低下。这时候其实最好是取一个概率分布使得尾部$[3,\infty)$的概率显著增大，而$Var(I)$显著减小，例如如果我们取$q(x)=(2\pi)^{-\frac{1}{2}}e^{-\frac{(x-4)^{2}}{2}}$，这时$Var(I)=0.0002$，方差大大降低了，收敛的速率也就越高。一般来说，在高维的时候，如果密度函数$p$，$f$很复杂的时候，寻找$q$就没那么容易了，高维度的困难似乎是这里面提到的所有蒙特卡罗方法的通病。

 

 

5.参考文献：

 

       [1]Larry Wasserman, All of Statistics: A Concise Course in Statistical Inference,

       [2]Kevin P. Murphy, Machine Learning A Probabilistic Perspective,2012 Massachusetts Institute of Technology