Lagrangian 对偶 和 Slater 条件

目录

• 1.Lagrange函数:
• 2.Lagrange对偶函数和对偶问题:
• 3.几何解释:
• 5.参考文献：

1.Lagrange函数:

   回忆上节的记号，对于任意一个优化问题（不一定是凸优化问题）： \begin{equation}\begin{split}\text{min}\quad \& f_{0}(x) \newline \text{subject to:}\quad \& f_{i}(x)\leq 0, i=1,...,m \newline \& h_{i}(x)=0, i=1,...,p\end{split}\end{equation} 我们可以看到，上述问题的真正难点就在于一组等式和不等式约束条件。所谓"拉格朗日对偶"的基本想法就是通过扩充目标函数，将原有问题中的目标函数$f_{0}$扩充为$f_{0}$以及约束函数的加权和，也就是将约束函数和原始的目标函数一并统一考虑，以达到简化约束条件的目的。   这时我们可以定义其Lagrange 函数： $$L: D \times\mathbb{R}^{m}\times\mathbb{R}^{p}\rightarrow \mathbb{R},$$ \begin{equation}L(x,\lambda,\nu)=f_{0}(x)+\sum_{i=1}^{m}\lambda_{i}f_{i}(x)+\sum_{i=1}^{p}\nu_{i}h_{i}(x).\end{equation}

这时我们称\(\lambda_{i}\)为对应于第\(i\)个不等式约束条件\(f_{i}\leq 0\)的拉格朗日乘子，称\(\nu_{i}\)为对应于第\(i\)个等式约束条件\(h_{i}= 0\)的拉格朗日乘子.

2.Lagrange对偶函数和对偶问题:

  我们定义Lagrange对偶函数：

\[g:\mathbb{R}^{m}\times\mathbb{R}^{p}\longrightarrow \mathbb{R}, \]

\begin{equation}g(\lambda,\nu)=\inf_{x\in D}L(x,\lambda,\nu)\end{equation}

值得注意的是，无论 \(f_{i}\), \(h_{i}\)是否为凸函数，Lagrange 对偶函数\(g\)都将是凹函数。另外，对于任意的\(x\in\mathbb{R}^{n}\)满足(1)中的约束条件以及\((\lambda,\nu)\in\mathbb{R}^{m}\times\mathbb{R}^{p}\),\(\lambda\succeq 0\)
\begin{split}g(\lambda,\nu)\leq L(x,\lambda,\nu)&=f_{0}(x)+\sum_{i=1}^{{m}\lambda_{i}f_{i}(x)+\sum_{i=1}}\nu_{i}h_{i}(x)\newline &\leq f_{0}(x),\end{split}
上式两边同时取下确界"\(\inf_{C}\)"我们得到：

\begin{equation}
g(\lambda,\nu)\leq p^{\ast}
\end{equation}

  现在我们考虑如下的优化问题：
\begin{equation}\begin{split}\max\quad & g(\lambda,\nu) \newline \text{subject to:}\quad & \lambda\succeq 0 \end{split}\end{equation}
则我们称该问题是原始问题(1)的"Lagrange对偶问题",简称"对偶问题"。

  这时我们设\(q^{\ast}\)为上述问题的最优值，即\(q^{\ast}=\sup_{\lbrace\lambda\succeq 0\rbrace}g(\lambda,\nu)\), 则由（4）可知\(q^{\ast}\leq p^{\ast}\)。我们再令\(d^{\ast}=p^{\ast}-q^{\ast}\), 称\(d^{\ast}\)为原问题和对偶问题之间的差距(gap). 进一步，如果\(d^{\ast}=0\),我们称原问题和对偶问题是强对偶的。

3.几何解释:

  为了建立一些几何直觉，我们定义集合：

\begin{equation}\mathcal{G}\triangleq\lbrace (f_{1}(x),...,f_{m}(x),h_{1}(x),...,h_{p}(x),f_{0}(x))\in \mathbb{R}^{{m}\times\mathbb{R}}\times\mathbb{R}\mid x\in D \rbrace\end{equation}

这时候很容易知道：

\begin{equation}p^{\ast}=\inf\lbrace t\mid (u,v,t)\in \mathcal{G}, u\preceq 0, v=0\rbrace\end{equation}

对于任意的\(\lambda\in\mathbb{R}^{m}\), \(\nu\in\mathbb{R}^{p}\), \(x\in D\), 过点\(p\triangleq (f_{1}(x),...,f_{m}(x),h_{1}(x),...,h_{p}(x),f_{0}(x))\)与向量\((\lambda,\nu,1)\)垂直的超平面为：

\[\lambda\cdot u+\nu\cdot v+t-L(x,\lambda,\nu)=0 \]

该超平面在\(t\)轴上的截距正好就是Lagrange函数在\((x,\lambda,\nu)\)处的取值！！！

  由以上观察我们容易得出\(g(\lambda,\nu)\)的几何意义：

\(g(\lambda,\nu)\)是与\((\lambda,\nu,1)\)垂直且与集合\(\mathcal{G}\)相交的超平面的t-截距的最小值!!!!,

（注意，“最小值”是不严谨的说法，其实应该是下确界，但是为了方便理解而这么将错就错，毕竟这里我们是形象描述！！！）

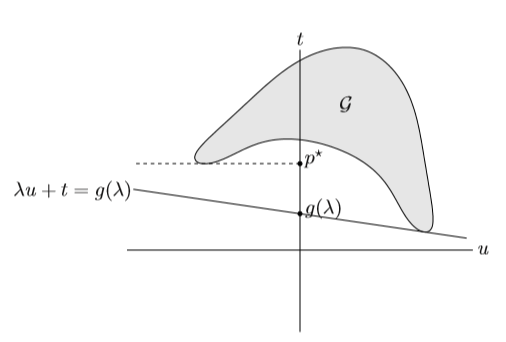
  如上图所示，在这里我们画出了一个无等式约束条件，二维情形下对应的示意图。如图所示，\(g(\lambda)\) 是以\(-t\)为斜率的一条直线在t轴上的截距。可以观察到该直线要是继续向下平移的话将不再和\(\mathcal{G}\)相交。同时我们注意到，当\(\lambda\geq 0\)时，\(g(\lambda)<p^{\ast}\)，这时\(gap\)严格大于零， 这似乎时是因为由于\(\mathcal{G}\)的非凸性并且\(\mathcal{G}\)的右半部分，也就是\(u\geq 0\)部分的最低点比左半部分更低造成的。

  为了研究方便，我们引入“上镜图”（Epigrah）的概念。我们定义集合：

\begin{equation}\mathcal{A}=\lbrace p+ (u,0,t)\in \mathbb{R}^{{m}\times\mathbb{R}}\times\mathbb{R}\mid p\in \mathcal{G}, u\in \mathbb{R}^{m},u\succeq 0, t\in \mathbb{R}, t\geq 0\rbrace\end{equation}
并称之为最优化问题(1)的上镜图（Epigrah)。容易看出，上镜图是由\(\mathcal{G}\)的一系列正向平移所构成。

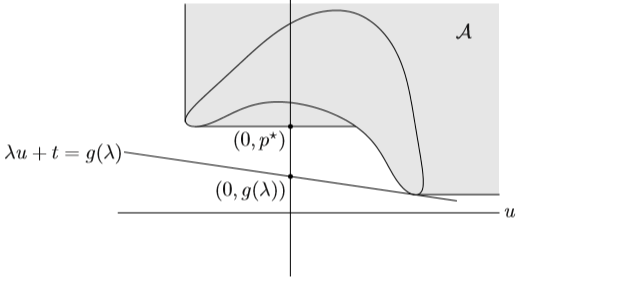
  如图所示，我们这里画出了和上图情形之下的上镜图\(\mathcal{A}\)的示意图。我们容易验证如下的性质：

性质1:如果原问题（1）是一个凸优化问题，也就是\(f_{i}\),i=0,..,m均为凸函数，而\(h_{i}\),i=1,...,p均为仿射函数的时候，其上镜图\(\mathcal{A}\)是一个凸集。

###4.Slater条件:
  有了以上的铺垫，我们可以介绍一个结果，它告诉我们，在什么样的条件下凸优化问题和其Lagrange对偶问题是强对偶的，也就是什么条件下我们可以将原问题进行转化。所幸的是，这个条件告诉我们，一般情况下强对偶是成立的，因为该条件很弱。

定理：如果原问题(1)是一个凸优化问题，存在\(\tilde{x}\in \text{relint} D\) 使得：\(f_{i}(\tilde{x})<0\), 对任意的\(i=1,...,m\), 则原问题和对偶问题是强对偶的。

证明：
   我们不妨假设仿射函数：
\(h_{i}(x)=\sum_{j=1}^{n}a_{ij}x_{j}+b_{i}\), 且矩阵\(A=(a_{ij})\)满足\(rank(A)=p\),否则我们可以进一步减少等式约束条件的数量，得到等价的凸优化问题，而\(d^{\ast}\)保持不变。

我们令集合：

\[\mathcal{B}=\lbrace (u,0,t)\in \mathbb{R}^{m}\times\mathbb{R}^{p}\times\mathbb{R}\mid u\preceq 0,t<p^{\ast} \rbrace$$, 此时$\mathcal{B}$与上镜集$\mathcal{A}$交集为空，它们均为凸集。于是由凸集分离定理，存在超平面分离两集合，也就是存在着$(\lambda_{0},\nu_{0},t_{0})\neq 0\in\mathbb{R}^{m}\times\mathbb{R}^{p}\times\mathbb{R}$以及$b\in\mathbb{R}$使得： 对任意的$x\in D$, $\xi \in \mathbb{R}_{+}^{m}$和$t\in\mathbb{R}_{+}$： \begin{equation}\sum_{i=1}^{m}\lambda_{0,i}(f_{i}(x)+\xi_{i})+\sum_{i=1}^{p}v_{0,i}h_{i}(x)+t_{0}(f_{0}(x)+t)\geq b\end{equation} 且对任意的$u\in \mathbb{R}^{m}$,$u\preceq 0$, $t<p^{\ast}$: \begin{equation}\lambda_{0}\cdot u+t_{0}t\leq b\end{equation} 由（9）中的任意性我们立即可以知道$\lambda_{0}\succeq 0$,$t_{0}\geq 0$, 这时我们令(10)中$u\rightarrow 0$,$t\rightarrow p^{\ast}$，可以知：$t_{0}p^{\ast}\leq b$，于是我们再结合（9）可知对任意$x\in D$： \begin{equation}\sum_{i=1}^{m}\lambda_{0,i}f_{i}(x)+\sum_{i=1}^{p}v_{0,i}h_{i}(x)+t_{0}f_{0}(x)\geq t_{0}p^{\ast}.\end{equation} 我们注意到，如果这时候$t_{0}>0$则上式两边同时除以$t_{0}$我们立即得到对任意的$x\in D$： $$L(x,\lambda_{0}/t_{0},\nu_{0}/t_{0})\geq p^{\ast},\]

这时我们立即得到：
\(g(\lambda_{0}/t_{0},\nu_{0}/t_{0})\geq p^{\ast}\), 于是强对偶成立。

此时我们假设\(t_{0}>0\)不成立，则\(t_{0}=0\),对任意\(x\in D\)：
\begin{equation}\sum_{i=1}^{{m}\lambda_{0,i}f_{i}(x)+\sum_{i=1}}v_{0,i}h_{i}(x)\geq 0.\end{equation}
这时由于\(\tilde{x}\in \text{relint} D\), 且\(f_{i}(\tilde{x})<0(i=1,...,m)\), 所以存在一个\(x\)在\(D\)的仿射闭包中的领域\(U\), \(U\subset D\)，且\(f_{i}<0(i=1,...,m)\)在D上恒成立,这时结合\(\lambda_{0,i}\geq 0\)我们立即知道对任意\(x\in U\)：
\begin{equation}\sum_{i=1}^{p}v_{0,i}h_{i}(x)\geq -\sum_{i=1}^{m}\lambda_{0,i}f_{i}(x)\geq 0\end{equation}
注意到仿射函数：\(\sum_{i=1}^{p}v_{0,i}h_{i}\)在\(\tilde{x}\)处取\(0\),如果它非恒为\(0\),则必然在\(U\)内取值有正有负，所以\(\sum_{i=1}^{p}v_{0,i}h_{i}\)恒为零，由假设\(rank(A)=p\)我们立即得到\(\nu_{0}=0\), 于是：
\begin{equation}\sum_{i=1}^{m}\lambda_{0,i}f_{i}(\tilde{x})\geq 0,\end{equation}
这时由于\(\lambda_{0,i}\geq 0\), \(f_{i}(\tilde{x})<0\), \(i=1,...,m\)我们立即得到\(\lambda_{0}=0\), 这与\((\lambda_{0},\nu_{0},t_{0})\neq 0\)矛盾，于是\(t_{0}\)必然大于0,命题得证。

5.参考文献：

Stephen Boyd，Lieven Vandenberghe：Convex Optimization，cambridge university press 2004，Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, S˜ao Paolo, Delhi