Codeforces Round #703 (Div. 2)
Codeforces Round #703 (Div. 2)
掉分场QAQ。
A. Shifting Stacks
题意:最开始有\(n\)个数,每次可以指定一个位置\(h_i>0\)且\(i<n\)的位置\(i\),让\(h_i-1\)并让\(h_{i+1}+1\),问能否通过操作使得\(h\)单调递增。
因为只要单调递增即可,因此我们可以只在第\(i\)个位置上保留\(i-1\)即可,把剩下多出来的无脑堆到后边去,如果发现\(i\)这个位置达不到\(i-1\)那么就无解,否则一定有解。
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 200005
#define int long long
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int T,n,a[N];
signed main()
{
T=read();
while(T--)
{
n=read();
for(int i=1;i<=n;i++)a[i]=read();
int ff=1;
for(int i=1;i<=n;i++)
{
if(a[i]<i-1)ff=0;
a[i+1]+=(a[i]-(i-1));
}
if(ff)puts("YES");
else puts("NO");
}
return 0;
}
B. Eastern Exhibition
这B题就是来搞心态的
题意:问有多少个整点能使得给出的\(n\)个点到这个点的曼哈顿距离和最小。
曼哈顿距离\(x,y\)是相互独立的,那么我们考虑一个点\((a,b)\),假设我们按\(x\)排序后,\(x_p\leq a\leq x_{p+1}\),按\(y\)排序后\(y_q\leq b\leq y_{q+1}\),那么距离和即为
注意到这实际上就是两个数轴上,到n个点距离和最小的式子,因此如果\(n\)为奇数直接取中位数即可,答案即为\(1\),如果\(n\)为偶数那么一定是取\(n/2\)到\(n/2+1\)这段区间内的数,\(x\)轴\(y\)轴的范围乘起来即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 200005
#define int long long
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int T,n,x[N],y[N];
signed main()
{
T=read();
while(T--)
{
n=read();
for(int i=1;i<=n;i++)x[i]=read(),y[i]=read();
sort(x+1,x+1+n);sort(y+1,y+1+n);
if(n%2)puts("1");
else printf("%lld\n",(x[n/2+1]-x[n/2]+1)*(y[n/2+1]-y[n/2]+1));
}
}
C. Guessing the Greatest
题意:交互题,每次可以询问一段区间内的次大值的位置,问整个序列最大值的位置。最多可问\(40(C1)\)/\(20(C2)\)次。
我们先考虑一个全局次大值\(x\),我们考虑全局最大值的位置在它的左边(右边是对称的),那么一定是这样的,设全局最大值位置为\(y\),那么一定有当\(a\leq y\)时\(query(a,x)=x\),否则\(query(a,x)\neq x\)。
有了这个性质于是就可以二分了,询问次数是\(\log\)级别的,可以在\(20\)次之内求出答案。
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 200005
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int n,cnt;
int query(int l,int r)
{
if(l==r)return 0;
printf("? %d %d\n",l,r);
fflush(stdout);
int res;
scanf("%d",&res);
return res;
}
int main()
{
scanf("%d",&n);
int l=1,r=n,now=query(1,n);
while(l<r)
{
int mid=(l+r)/2;
if(now<=mid)
{
if(query(1,mid)==now)r=mid;
else l=mid+1;
}
else
{
if(query(mid+1,n)==now)l=mid+1;
else r=mid;
}
}
printf("! %d\n",l);
fflush(stdout);return 0;
}
D. Max Median
题意:求长度不小于\(k\)的中位数最大的子串,求中位数。
考虑二分答案\(x\),那么对于一个字串,一定是大于等于\(x\)的数越多越好,且来一个大于等于\(x\)的数可以和一个小于\(x\)的数的贡献抵消,因此将大于等于\(x\)的数的贡献设为\(1\),否则为\(-1\),那么问题就变成了求一个区间和大于\(0\)的长度不小于\(k\)的子段,前缀和即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 200005
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int n,k,a[N],s[N],minn[N];
int check(int x)
{
for(int i=1;i<=n;i++)s[i]=s[i-1]+((a[i]>=x)?1:-1);
for(int i=1;i<=n;i++)minn[i]=min(minn[i-1],s[i]);
int res=-1e9;
for(int i=k;i<=n;i++)res=max(res,s[i]-minn[i-k]);
return res>0;
}
int main()
{
n=read();k=read();
for(int i=1;i<=n;i++)a[i]=read();
int l=0,r=1e9;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid))l=mid+1;
else r=mid-1;
}
printf("%d\n",l-1);
}
E. Paired Payment
题意:给一张带权无向图,如果原图上有两条边\((a,b,c)\)和\((b,d,e)\),那么你可以从\(a\)走到\(d\),花费为\((c+e)^2\),边权最多\(50\)。
考虑暴力拆点,把一个点拆为一个能正常走到的点和\(50\)个中转点,那么对于一个状态\(sta(i,c)\),表示\(i\)号点状态为\(c\),如果\(c=0\)那么为正常走到的点,否则表示通过一条边权为\(c\)的点走过来的状态。
那么设\(dis(i,j)\)表示走到\(sta(i,j)\)的最短路,转移的时候看是否是中转点,即\(j\)是否等于\(0\),如果是正常点就转移到下一个点的中转状态,否则转移到下一个点的正常状态,再走到正常状态的时候结算一下这两条边的贡献即可。
直接大力\(dij\)即可。
#pragma GCC optimize(3,"Ofast","inline")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define N 400005
#define mp make_pair
#define P pair<int,pair<int,int> >
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int n,m,v[N],w[N],head[N],nxt[N],cnt,f[N/2][51],vis[N/2][51];
void add(int a,int b,int c)
{
v[++cnt]=b;
w[cnt]=c;
nxt[cnt]=head[a];
head[a]=cnt;
}
void dij()
{
memset(f,0x3f,sizeof(f));
priority_queue<P,vector<P>,greater<P> >q;
q.push(mp(0,mp(1,0)));
f[1][0]=0;
while(!q.empty())
{
pair<int,int>c=q.top().second;
q.pop();int x=c.first,y=c.second;
if(vis[x][y])continue;
for(int i=head[x];i;i=nxt[i])
{
if(y==0)
{
if(f[v[i]][w[i]]>f[x][y])
{
f[v[i]][w[i]]=f[x][y];
q.push(mp(f[v[i]][w[i]],mp(v[i],w[i])));
}
}
else
{
if(f[v[i]][0]>f[x][y]+(y+w[i])*(y+w[i]))
{
f[v[i]][0]=f[x][y]+(y+w[i])*(y+w[i]);
q.push(mp(f[v[i]][0],mp(v[i],0)));
}
}
}
}
}
int main()
{
n=read();m=read();
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),z=read();
add(x,y,z);add(y,x,z);
}
dij();
for(int i=1;i<=n;i++)
{
if(f[i][0]==0x3f3f3f3f)printf("-1 ");
else printf("%d ",f[i][0]);
}
return 0;
}
F. Pairs of Paths
题意:给一棵\(n\)个结点的树和\(m\)条路径,问有多少对路径相交部分有些只有一个顶点。
满足题意的两条路径的交点必然是其中某条路径的端点的\(lca\)。
不然的话从这个交点往上跳一步还是交点,因此不符合要求。
那么就有这两种情况
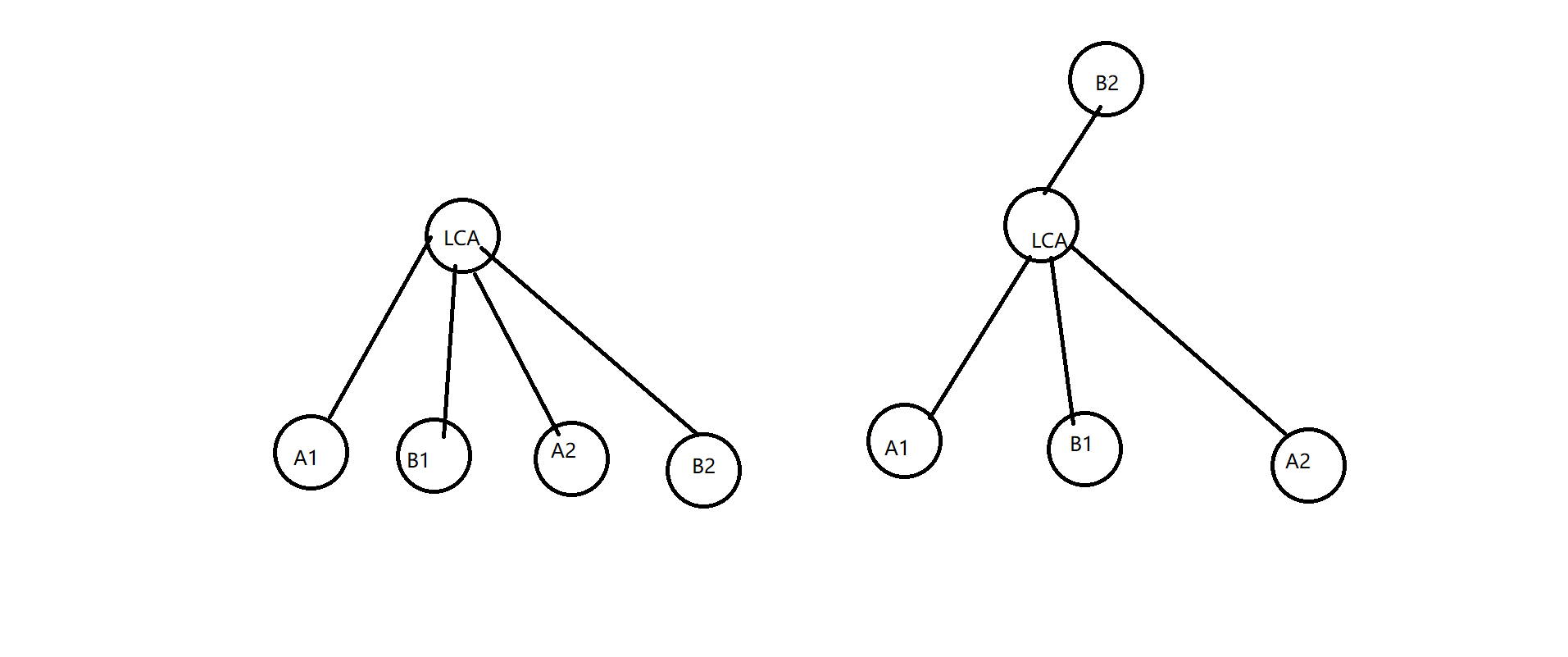
要么是LCA在同一处,要么是在不同处。
先考虑在同一处的情况,对于每一个点我们计算LCA为当前点的答案,那么我们只需要顺序扫过去,记录每个点所在的子树,然后开个桶减掉不合法的即可。具体来说就记\(b_i\)为\(i\)号子树中有多少条链,我们先让\(x < y\),(x和y是两个端点所在的子树),然后按\(x\)排序,我们只需要每次加前边的链数之后减去\(b[y]\)即可。
不在同一处的情况比较简单,就直接统计一颗子树内有多少个端点即可,按照\(LCA\)的深度排序后可以用树状数组维护,注意要减掉来自这个链两端所在子树的贡献。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 600005
#define lowbit(x) x&-x
#define mp make_pair
#define int long long
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int n,m,tot,v[N],head[N],nxt[N],cnt,dfn[N],dfstime,fa[N][25],dep[N],rfn[N],b[N],ans;
struct node
{
int lca,a,b,x,y;
}q[N];
struct BIT
{
int c[N];
void modify(int x,int k){for(;x<=n;x+=lowbit(x))c[x]+=k;}
int query(int x){int res=0;for(;x;x-=lowbit(x))res+=c[x];return res;}
}t;
void add(int a,int b)
{
v[++cnt]=b;
nxt[cnt]=head[a];
head[a]=cnt;
}
void dfs(int x,int fath)
{
dep[x]=dep[fath]+1;dfn[x]=++dfstime;
for(int i=0;i<=19;i++)fa[x][i+1]=fa[fa[x][i]][i];
for(int i=head[x];i;i=nxt[i])
{
if(v[i]==fath)continue;
fa[v[i]][0]=x;
dfs(v[i],x);
}
rfn[x]=dfstime;
}
pair<int,int> lca(int x,int y)
{
if(x==y)return mp(-1,-1);
int ff=0;
if(dep[x]<dep[y])swap(x,y),ff=1;
int X=x;
for(int i=20;i>=0;i--)
{
if(dep[fa[x][i]]>=dep[y])x=fa[x][i];
}
if(x==y)
{
x=X;
int D=dep[x]-dep[y]-1;
//cout<<x<<" "<<D<<endl;
for(int i=20;i>=0;i--)if(D>=(1<<i))D-=(1<<i),x=fa[x][i];
if(ff)return mp(-1,x);
else return mp(x,-1);
}
for(int i=20;i>=0;i--)
{
if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
}
if(ff)swap(x,y);
return mp(x,y);
}
int cmp(node a,node b)
{
if(dep[a.lca]!=dep[b.lca])return dep[a.lca]<dep[b.lca];
if(a.lca!=b.lca)return a.lca<b.lca;
if(a.a!=b.a)return a.a>b.a;
return a.b>b.b;
}
signed main()
{
n=read();tot=n;
for(int i=1;i<n;i++)
{
int x=read(),y=read();
add(x,y);add(y,x);
}
dfs(1,0);m=read();
//cout<<"!!!"<<fa[3][0]<<endl;
for(int i=1;i<=m;i++)
{
q[i].x=read();q[i].y=read();
pair<int,int>tmp=lca(q[i].x,q[i].y);
q[i].a=((tmp.first==-1)?(++tot):tmp.first);
q[i].b=((tmp.second==-1)?(++tot):tmp.second);
if(tmp.first!=-1&&tmp.second!=-1)q[i].lca=fa[tmp.first][0];
else if(max(tmp.first,tmp.second)>0)q[i].lca=fa[max(tmp.first,tmp.second)][0];
else q[i].lca=q[i].x;
//cout<<"LCA="<<q[i].lca<<" "<<tmp.first<<" "<<tmp.second<<endl;;
if(q[i].a>q[i].b)swap(q[i].a,q[i].b),swap(q[i].x,q[i].y);
}
sort(q+1,q+1+m,cmp);
//for(int i=1;i<=m;i++)cout<<q[i].x<<" "<<q[i].y<<" "<<q[i].a<<" "<<q[i].b<<" "<<q[i].lca<<endl;
//puts("");
for(int i=1;i<=m;i++)
{
int j=i,sum=0;while(j<m&&q[j+1].lca==q[j].lca)j++;
for(int k=i;k<=j;k++)
{
int L=k;while(L<j&&q[L+1].a==q[k].a)L++;
for(int p=k;p<=L;p++)ans+=sum-b[q[p].b];
for(int p=k;p<=L;p++)b[q[p].a]++,b[q[p].b]++;
sum+=L-k+1;
k=L;
}
for(int k=i;k<=j;k++)
{
ans+=t.query(rfn[q[k].lca])-t.query(dfn[q[k].lca]-1);
//cout<<ans<<endl;
if(q[k].a<=n)ans-=t.query(rfn[q[k].a])-t.query(dfn[q[k].a]-1);
if(q[k].b<=n)ans-=t.query(rfn[q[k].b])-t.query(dfn[q[k].b]-1);
//cout<<t.query(rfn[q[k].a])-t.query(dfn[q[k].a]-1)<<endl;
}
for(int k=i;k<=j;k++)t.modify(dfn[q[k].x],1),t.modify(dfn[q[k].y],1);
i=j;
}
printf("%lld\n",ans);
}


