[NOIP2016PJ]魔法阵

今天模拟赛的题，，，唯一没有Giao出来的题（不然我就AKIOI了~）

最开始没想到数学题，把所有部分分都说一遍吧：

35分：纯暴力O(M^4)枚举，对于每一组a,b,c,d验证其是否合法。

60分：经过读题，不难发现a,b,c,d单调递增，可以考虑对其进行排序后再暴力枚举，枚举量减少近一半。

85分：对xb-xa=2(xd-xc)进行分析，可以得到以下公式：double((xb-xa+2xc)/2)=double(xd)，再查找是否存在xd，这样我们只需枚举a,b,c，时间复杂度是O(M^3)

100分：依旧是对xb-xa=2(xd-xc)进行分析，我们设t=xd-xc，则xb-xa=2⋅t；再分析第二个条件Xb−Xa<(Xc−Xb)/3，我们可以得到Xc−Xb>6⋅t，我们给他补全成等号，就是Xc−Xb=6⋅t+k

所以这四个数在数轴上的排列如图所示（图片来自博客园）

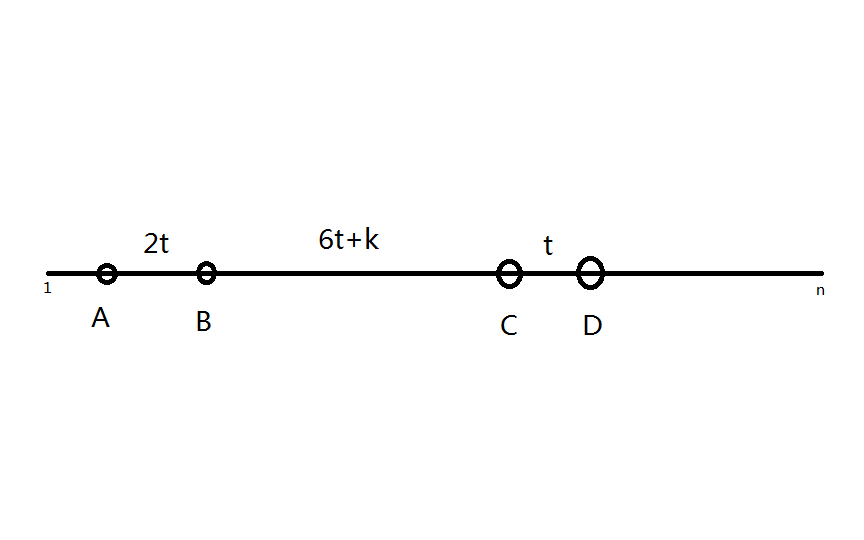
所以我们会有一个不成熟的思路：在1-n/9范围内枚举t，把a,b,c,d拿t表示出来。

那么如何计算呢？枚举D。当我们枚举到一个D值的时候，与之对应的C值是确定的（不受k影响），而A值和B值却不一定。因此我们可以找到最大的与之对应的A值B值。

但是有可能会存在一组AB值要比当前计算到的小，怎么办呢？不妨设有可能存在的比最大值小的A值为A1，B值为B1，计算到的为A2和B2

当A1<A2&&B1<B2时，只要A2和B2能组成魔法阵，A1和B1一定可以（k只是大于0的数，而对k的上界没有限制，当我们把k放大时，就可以构造出A1和B1了）。

由于是顺序枚举，所以我们可以记录一下之前有多少组合法解（类似于前缀和），最后再用乘法原理计算。同样的方法，我们从A的上界往A的下界枚举记录后缀和然后计算即可。

下面给出参考代码：

 

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 50005
#define M 50005
using namespace std;
int n,m,ans[M][10],num[M],a[M],A,B,C,D;
int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=0;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    if(f)return x;return -x;
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++)
    {
        a[i]=read();
        num[a[i]]++;
    }
    for(int t=1;t*9<n;t++)
    {
        int sum=0;
        for(D=9*t+2;D<=n;D++)
        {
            C=D-t;
            B=C-6*t-1;
            A=B-2*t;
            sum+=num[A]*num[B];
            ans[C][3]+=num[D]*sum;
            ans[D][4]+=num[C]*sum;
        }
        sum=A=B=C=D=0;
        for(A=n-t*9-1;A>=1;A--)
        {
            B=A+2*t;
            C=B+6*t+1;
            D=C+t;
            sum+=num[C]*num[D];
            ans[A][1]+=num[B]*sum;
            ans[B][2]+=num[A]*sum;
        }
    }
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=4;j++)
        {
            cout<<ans[a[i]][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}