网络流初步——最大流问题

#网络流的概念#

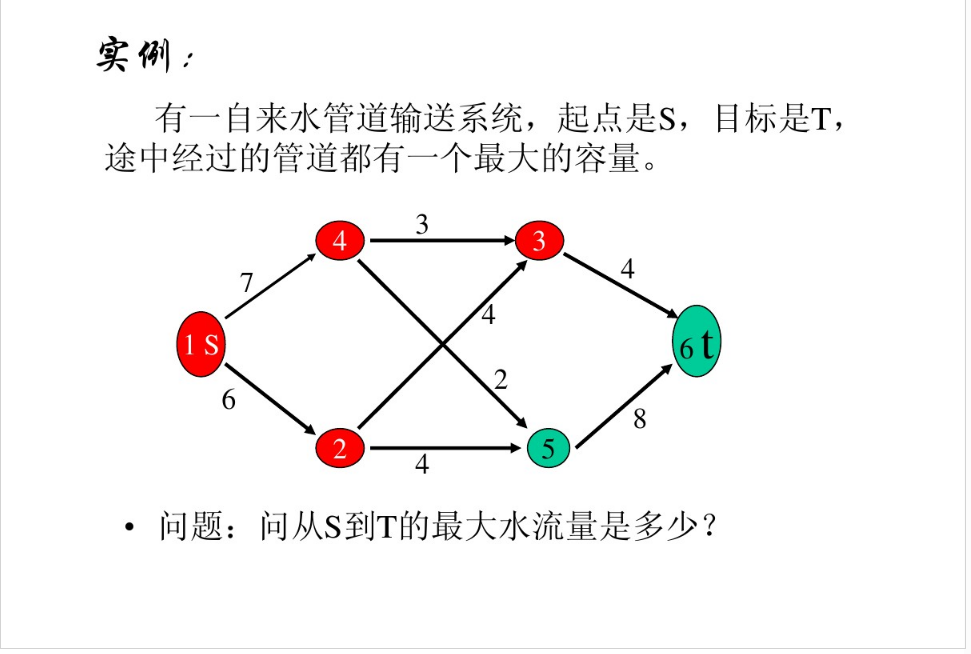
网络流(network-flows)是一种类比水流的解决问题方法，与线性规划密切相关。网络流的理论和应用在不断发展，出现了具有增益的流、多终端流、多商品流以及网络流的分解与合成等新课题。网络流的应用已遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等众多领域。（摘自百度百科）
形象理解：就好比你家小区的供水系统，所有的水都来自自来水厂，经过管道运输到你小区的用户，再经过下水道去往废水处理厂，整个过程中，自来水厂就好比源点，整个网络中的管道大小限制就好比容量，其中流过的水量好比流量，而最终的处理厂就好比汇点。
  

#网络流的基本定义及性质#

·网络流:所有弧上流量的集合f={f(u,v)},称为该容量网络的一个网络流.

定义：带权的有向图G=(V,E)，满足以下条件，则称为网络流图(flow network)：网络流主要解决流量问题。

源点：整个网络流图中只有一个入度为0的点，它“制造”流量，并通过边发送给其他的节点。

汇点：整个网络流图中只有一个出度为0的点，它“消耗”流量。

容量：每条边可以通过的最多流量。

·性质:

1、容量限制：0≤f(u,v)≤c(u,v),其中f为流量，c为容量。

2、斜对称性：f(u,v)=-f(v,u)

3、流量平衡：即流入一个非s,t节点的流量等于流出该点的流量。

·残量网络：残量网络=容量网络-流量网络

#最大流的性质以及相关算法#

1、可行流：在容量网络G中满足以下条件的网络流f,称为可行流:

·弧流量限制条件: 0<=f(u,v)<=c(u,v);

·平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外).

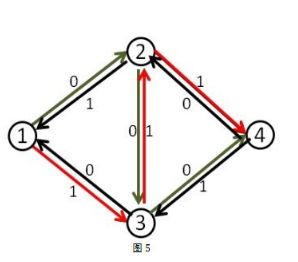
如下图：两种流量均为可行流，第二种方式是该网络的最大流。（边上数字为容量，框内数字为流量）

 

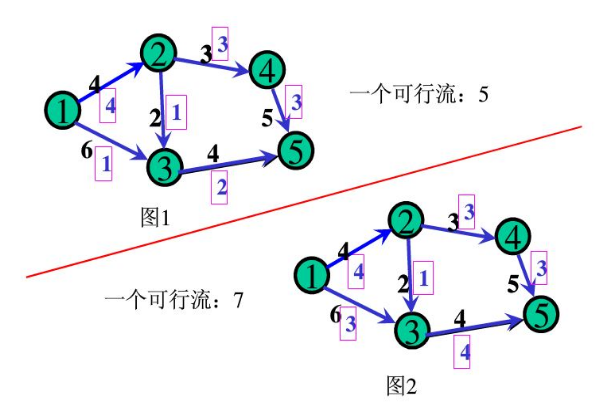
2、最大流：顾名思义，可行流中流量最大的流称为最大流。（最大流可能不唯一）

3、增广路：从s到t的一条路径，经过的每一条边流量均未满，沿着增广路增加流量的过程叫做增广，显然，当网络中没有增广路的时候，流量达到了最大，所以如何高效快速地找出所有增广路是最大流算法需要解决的问题。

4、最大流相关算法：

·EK算法

1、引入反向边：请看下图：

假设我们第一次沿着1->2->3->4这条增广路增广，将每条边的流量增加1，之后我们就得到下面这张图：

 

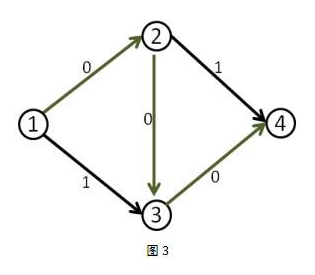
之后这张图就没有增广路了，算法结束，，，然而有眼睛的我们都知道，这个网络的最大流明显是2。

引入反向边后，我们就可以给程序一个反悔的机会！！！

如下图所示：加入反边后可以让程序把之前增广的流量推掉~,从而得到正确答案

 

 

 

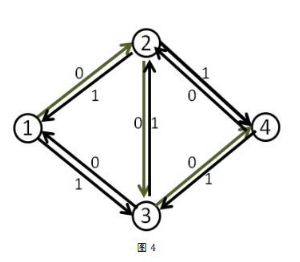
之后bfs延最短路(每个边边权看成1)增广直到没有增广路即可。

EK算法参考代码如下：

 

 1 #include<iostream>
 2 #include<cstring>
 3 #include<queue>
 4 #include<cstdio>
 5 #define N 200005
 6 using namespace std;
 7 int read()
 8 {
 9     int x=0,f=1;char ch=getchar();
10     while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
11     while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
12     return x*f;
13 }
14 int n,m,x,y,z,v[N],w[N],head[N],nxt[N],cnt,s,t,pre[N],prepath[N];
15 bool vis[N];
16 void add(int a,int b,int c)
17 {
18     v[cnt]=b;
19     w[cnt]=c;
20     nxt[cnt]=head[a];
21     head[a]=cnt;
22     cnt++;
23 }
24 int bfs()
25 {
26     memset(vis,0,sizeof(vis));
27     memset(pre,-1,sizeof(pre));
28     memset(prepath,-1,sizeof(prepath));
29     queue<int>q;
30     q.push(s);
31     vis[s]=1;
32     while(!q.empty())
33     {
34         int c=q.front();
35         q.pop();
36         for(int i=head[c];i!=-1;i=nxt[i])
37         {
38             int d=v[i];
39             if(!vis[d]&&w[i])
40             {
41                 pre[d]=c;
42                 prepath[d]=i;
43                 if(d==t)return 21374404;
44                 vis[d]=1;
45                 q.push(d);
46             }
47         }
48     }
49     return 0;
50 }
51 int EK()
52 {
53     int maxflow=0;
54     while(bfs())
55     {
56         int MIN=21374404;
57         for(int i=t;i!=s;i=pre[i])MIN=min(MIN,w[prepath[i]]);
58         for(int i=t;i!=s;i=pre[i])
59         {
60             w[prepath[i]]-=MIN;
61             w[prepath[i]^1]+=MIN;
62         }
63         maxflow+=MIN;
64         //cout<<"----------------------------------"<<endl;
65     }
66     return maxflow;
67 }
68 int main()
69 {
70     memset(head,-1,sizeof(head));
71     m=read();n=read();
72     s=1;t=n;
73     for(int i=1;i<=m;i++)
74     {
75         x=read();y=read();z=read();
76         add(x,y,z);add(y,x,0);
77     }
78     cout<<EK()<<endl;
79     return 0;
80 }
View Code

 

 

 

·Dinic算法

EK算法的时间复杂度可能高达O(NM2)，即使在绝大多数情况下达不到理论上界，但是狠心的出题人绝对会出数据卡EK......

考虑多路增广。

这点使得Dinic的时间复杂度可以锐减至O(N2M),而实现Dinic的方法是BFS分层+DFS增广，BFS分层后，我们就有了每个点的层数编号，对任意点u到点d的路径如果有dep[d]==dep[u]+1，我们就可以判断该路径在一条最短增广路上。

我们就可以进行增广，达到一次分层多次增广的效果。

下面给出Dinic算法参考代码：

 

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<queue>
 5 #define M 500005
 6 #define N 100005
 7 #define inf 21374404
 8 using namespace std;
 9 int read()
10 {
11     int x=0,f=1;char ch=getchar();
12     while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
13     while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
14     return x*f;
15 }
16 int n,m,s,t,v[M],w[M],head[M],nxt[M],cnt=-1,x,y,z,dep[N];
17 bool vis[N];
18 void add(int a,int b,int c)
19 {
20     v[++cnt]=b;
21     w[cnt]=c;
22     nxt[cnt]=head[a];
23     head[a]=cnt;
24 }
25 int bfs()
26 {
27     memset(dep,0x3f,sizeof(dep));
28     memset(vis,0,sizeof(vis));
29     dep[s]=0;
30     queue<int>q;
31     q.push(s);
32     while(!q.empty())
33     {
34         int c=q.front();
35         q.pop();
36         vis[c]=0;
37         for(int i=head[c];i!=-1;i=nxt[i])
38         {
39             int d=v[i];
40             if(dep[d]>dep[c]+1&&w[i])
41             {
42                 dep[d]=dep[c]+1;
43                 if(!vis[d])
44                 {
45                     q.push(d);
46                     vis[d]=1;
47                 }
48             }
49         }
50     }
51     if(dep[t]!=0x3f3f3f3f)return 1;
52     return 0;
53 }
54 int dfs(int node,int low)
55 {
56     int rlow;
57     if(node==t)return low;
58     for(int i=head[node];i!=-1;i=nxt[i])
59     {
60         int d=v[i];
61         if(dep[d]==dep[node]+1&&w[i])
62         {
63             if(rlow=dfs(d,min(low,w[i])))
64             {
65                 w[i]-=rlow;
66                 w[i^1]+=rlow;
67                 return rlow;
68             }
69         }
70     }
71     return 0;
72 }
73 int Dinic()
74 {
75     int maxflow=0,lowflow;
76     while(bfs())
77     {
78         if(lowflow=dfs(s,inf))
79         {
80             maxflow+=lowflow;
81         }
82     }
83     return maxflow;
84 }
85 int main()
86 {
87     memset(head,-1,sizeof(head));
88     m=read();n=read();s=1;t=n;
89     for(int i=1;i<=m;i++)
90     {
91         x=read();y=read();z=read();
92         add(x,y,z);add(y,x,0);
93     }
94     cout<<Dinic()<<endl;
95     return 0;
96 }
View Code

 

 

 

 本博客部分内容摘自以下网址

https://blog.csdn.net/mystery_guest/article/details/51910913

https://mbd.baidu.com/newspage/data/landingsuper?context=%7B%22nid%22%3A%22news_10014940531206828082%22%7D&n_type=1&p_from=3

https://baike.baidu.com/item/%E7%BD%91%E7%BB%9C%E6%B5%81/2987528?fr=aladdin#2

 

 

 

posted @ 2019-07-19 14:07  shao0320  阅读(1284)  评论(1)  编辑  收藏  举报
****************************************** 页脚Html代码 ******************************************