浅析树链剖分
树链剖分用来解静态树上维护路径信息的问题,例如:给定一颗点带权的树,每次去修改某条路径上所有点的点权,或是求某条路径上的点权之和,当这棵树的形态为一条链时,这实际上就是一个区间修改求和的问题,可以用线段树等数据结构方便地求解。对于其他的情况,由于树的形态不变,因此树链剖分的策略是把这棵树恰当的剖分为若干条链,每一条链就对应线段树里的一段区间,此时就可以利用线段树等进行解决了。
也许对于以上的概念你读不太懂,不过没关系,先来看看几个问题:
1、将树上x号节点到y号节点的路径上每一个节点权值增加z;
2、求树从x到y结点最短路径上所有节点的值之和
这两个问题分开来看都不是很难,但是组合起来就不好办了。这时我们需要引入一种新的方法:
树链剖分!
就像概念中说的一样,当这棵树是一条链时,只需要一个线段树就可以解决了。下面我们看一看树链剖分的基本操作:
首先我们要明确几个概念(万恶的概念QWQ):
1、重儿子:非叶节点的儿子中子节点最多的叫做该节点的重儿子。
2、轻儿子:除了重儿子剩下的儿子就是轻儿子
3、重边:连接某节点与它的重儿子的边叫重边
4、重链:一些重边组成的链叫重链。
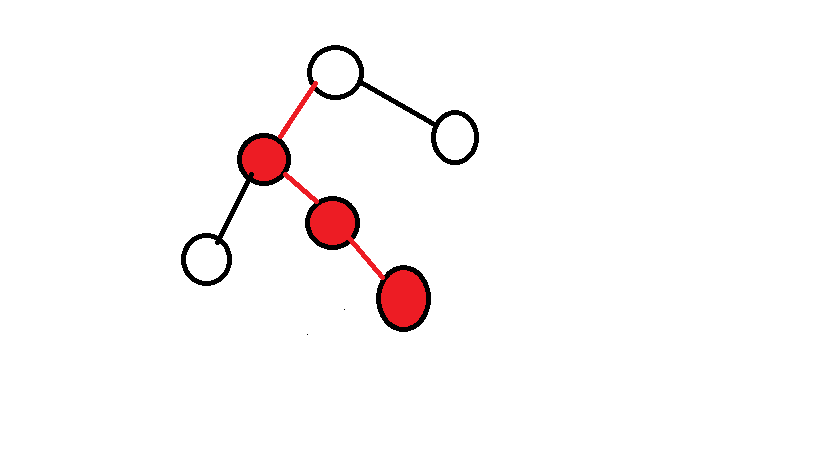
图中标红的节点即为父节点的重儿子,标红的边即为重边。
注意:重链的端点一定是轻儿子或根节点。
在剖分的之前中要预处理计算出以下六个数组:
dep[x]:x的深度
fa[x]:x的父亲
size[x]:x的子树大小
son[x]:x的重儿子
top[x]:x所在重链的顶部节点(深度最小)
seg[x]:x在线段树中的下标(优先遍历重儿子的dfs序)
对于前4个值我们可以进行一遍dfs,对于后2个值我们可以进行第二遍dfs......
两遍dfs参考代码:
1 void dfs1(int node,int father) 2 { 3 fa[node]=father; 4 dep[node]=dep[father]+1; 5 size[node]=1; 6 int maxson=-1; 7 for(int i=head[node];i;i=nxt[i]) 8 { 9 int go=v[i]; 10 if(go==father)continue; 11 dfs1(go,node); 12 size[node]+=size[go]; 13 if(size[go]>maxson)son[node]=go,maxson=size[go]; 14 } 15 } 16 void dfs2(int node,int topfather) 17 { 18 seg[node]=++id; 19 top[node]=topfather; 20 w[id]=num[node]; 21 if(!son[node])return; 22 dfs2(son[node],topfather); 23 for(int i=head[node];i;i=nxt[i]) 24 { 25 int go=v[i]; 26 if(go==fa[node]||go==son[node])continue; 27 dfs2(go,go);//轻儿子是重链的顶端. 28 } 29 }
预处理出以上6个值后,我们就可以正式开始树链剖分了。
(1)树链剖分改路径权值:
对于任意节点x,y,LCA(x,y)存在且唯一,所以它一定在某条重链上(单独一个节点也算一条重链)于是我们就可以让x,y中较深的那一个节点跳到它所在重链的端点父亲位置,直到x,y在同一条重链上,因为第二次深度优先搜索优先遍历重儿子,所以同一条重链DFS序是连续的,也就是他们对应在线段树中的下标是连续的,就转化成了一个区间修改的问题,每次跳的时候修改seg[top[x]~seg[x]的权值即可。
树链剖分改路径权值参考代码:
1 void Tadd(int x,int y) 2 { 3 z%=p; 4 while(top[x]!=top[y]) 5 { 6 if(dep[top[x]]<dep[top[y]])swap(x,y); 7 add(seg[top[x]],seg[x],1); 8 x=fa[top[x]]; 9 } 10 if(dep[x]>dep[y])swap(x,y); 11 add(seg[x],seg[y],1); 12 }
(2)树链剖分改子树权值:
由于是深度优先搜索,所以同一子树的DFS序也是连续的,以x为根节点子树的大小为size[x],所以对应的区间为seg[x]~seg[x]+size[x]-1,区间修改即可。
树链剖分改子树权值代码:
1 void Treeadd(int x,int z) 2 { 3 add(seg[x],seg[x]+size[x]-1,1); 4 }
注意:区间修改+区间求和的操作需要标记永久化或标记下传。
完整代码:

1 #include<iostream> 2 #include<cstdio> 3 #define N 100005 4 #define M 200005 5 #define int long long 6 #define mid (l+r)/2 7 #define lc k*2 8 #define rc k*2+1 9 using namespace std; 10 struct node 11 { 12 int l,r,w,tag; 13 }tree[4*N]; 14 int v[M],head[M],nxt[M],cnt;//邻接表 15 int n,m,r,p;//树的结点个数、操作个数、根节点序号和取模数 16 int q,x,y,z,num[N],w[N]; 17 int dep[N],fa[N],size[N],son[N],top[N],seg[N],id; 18 //dep[x] x的深度 19 //fa[x] x的父亲 20 //size[x] x的子树大小 21 //son[x] x的重儿子 22 //top[x] x所在重链的顶部节点(深度最小) 23 //seg[x] x在线段树中的下标 24 int read() 25 { 26 int x=0,f=1;char ch=getchar(); 27 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 28 while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 29 return x*f; 30 } 31 void add(int a,int b) 32 { 33 v[++cnt]=b; 34 nxt[cnt]=head[a]; 35 head[a]=cnt; 36 } 37 //-------------以上为基础操作以及定义----------------- 38 //-------------以下为线段树--------------------------- 39 void build(int l,int r,int k) 40 { 41 tree[k].l=l;tree[k].r=r; 42 if(l==r) 43 { 44 tree[k].w=w[l]%p; 45 return; 46 } 47 build(l,mid,lc); 48 build(mid+1,r,rc); 49 tree[k].w=(tree[lc].w+tree[rc].w)%p; 50 } 51 int query(int x,int y,int k) 52 { 53 int l=tree[k].l,r=tree[k].r; 54 if(l>=x&&r<=y) 55 { 56 return (tree[k].w+tree[k].tag*(r-l+1))%p; 57 } 58 int res=tree[k].tag*(min(r,y)-max(l,x)+1); 59 if(x<=mid)res+=query(x,y,lc),res%=p; 60 if(y>mid)res+=query(x,y,rc),res%=p; 61 return res%p; 62 } 63 void add(int x,int y,int k) 64 { 65 int l=tree[k].l,r=tree[k].r; 66 if(l>=x&&r<=y) 67 { 68 tree[k].tag+=z; 69 return; 70 } 71 tree[k].w+=(min(r,y)-max(l,x)+1)*z; 72 if(x<=mid)add(x,y,lc); 73 if(y>mid)add(x,y,rc); 74 } 75 //---------------以上为线段树------------------ 76 //---------------以下为树链剖分---------------- 77 void Tadd(int x,int y) 78 { 79 z%=p; 80 while(top[x]!=top[y]) 81 { 82 if(dep[top[x]]<dep[top[y]])swap(x,y); 83 add(seg[top[x]],seg[x],1); 84 x=fa[top[x]]; 85 } 86 if(dep[x]>dep[y])swap(x,y); 87 add(seg[x],seg[y],1); 88 } 89 int Tquery(int x,int y) 90 { 91 int res=0; 92 while(top[x]!=top[y]) 93 { 94 if(dep[top[x]]<dep[top[y]])swap(x,y); 95 res+=query(seg[top[x]],seg[x],1); 96 res%=p; 97 x=fa[top[x]]; 98 } 99 if(dep[x]>dep[y])swap(x,y); 100 res+=query(seg[x],seg[y],1); 101 return res%p; 102 } 103 void Treeadd(int x,int z) 104 { 105 add(seg[x],seg[x]+size[x]-1,1); 106 } 107 int Treequery(int x) 108 { 109 return query(seg[x],seg[x]+size[x]-1,1); 110 } 111 //---------------以上为树链剖分---------------- 112 //---------------以下为预处理------------------ 113 void dfs1(int node,int father) 114 { 115 fa[node]=father; 116 dep[node]=dep[father]+1; 117 size[node]=1; 118 int maxson=-1; 119 for(int i=head[node];i;i=nxt[i]) 120 { 121 int go=v[i]; 122 if(go==father)continue; 123 dfs1(go,node); 124 size[node]+=size[go]; 125 if(size[go]>maxson)son[node]=go,maxson=size[go]; 126 } 127 } 128 void dfs2(int node,int topfather) 129 { 130 seg[node]=++id; 131 top[node]=topfather; 132 w[id]=num[node]; 133 if(!son[node])return; 134 dfs2(son[node],topfather); 135 for(int i=head[node];i;i=nxt[i]) 136 { 137 int go=v[i]; 138 if(go==fa[node]||go==son[node])continue; 139 dfs2(go,go);//轻儿子是重链的顶端. 140 } 141 } 142 //---------------以上为预处理------------------ 143 //---------------以下为主函数------------------ 144 signed main() 145 { 146 //freopen("1.in","r",stdin); 147 n=read();m=read();r=read();p=read(); 148 for(int i=1;i<=n;i++)num[i]=read(); 149 for(int i=1;i<n;i++) 150 { 151 x=read();y=read(); 152 add(x,y);add(y,x); 153 } 154 dfs1(r,0);dfs2(r,r); 155 build(1,n,1); 156 while(m--) 157 { 158 q=read(); 159 if(q==1) 160 { 161 x=read();y=read();z=read(); 162 Tadd(x,y); 163 } 164 else if(q==2) 165 { 166 x=read();y=read(); 167 cout<<Tquery(x,y)<<endl; 168 } 169 else if(q==3) 170 { 171 x=read();z=read(); 172 Treeadd(x,z); 173 } 174 else 175 { 176 x=read(); 177 cout<<Treequery(x)<<endl; 178 } 179 180 } 181 return 0; 182 }



