P5020 货币系统

题目描述

在网友的国度中共有 n 种不同面额的货币，第 i 种货币的面额为 a[i]，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 n、面额数组为a[1..n] 的货币系统记作 (n,a)。

在一个完善的货币系统中，每一个非负整数的金额 x 都应该可以被表示出，即对每一个非负整数 x，都存在 n个非负整数 t[i]满足a[i]×t[i] 的和为 x。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额 x不能被该货币系统表示出。例如在货币系统 n=3, a=[2,5,9] 中，金额 1,3 就无法被表示出来。

两个货币系统 (n,a) 和 (m,b) 是等价的，当且仅当对于任意非负整数 x，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b)，满足 (m,b) 与原来的货币系统 (n,a)等价，且 m 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 m。

输入输出格式

输入格式：

输入文件的第一行包含一个整数 T，表示数据的组数。

接下来按照如下格式分别给出 T 组数据。 每组数据的第一行包含一个正整数 n。接下来一行包含 n 个由空格隔开的正整数 a[i]。

输出格式：

输出文件共有 T 行，对于每组数据，输出一行一个正整数，表示所有与 (n,a)等价的货币系统 (m,b) 中，最小的 m。

输入输出样例

输入样例#1： 

2 
4 
3 19 10 6 
5 
11 29 13 19 17 

输出样例#1： 

2   
5  

说明

在第一组数据中，货币系统 (2, [3,10])和给出的货币系统 (n,a) 等价，并可以验证不存在m < 2的等价的货币系统，因此答案为2。在第二组数据中，可以验证不存在m < n的等价的货币系统，因此答案为5。

【数据范围与约定】

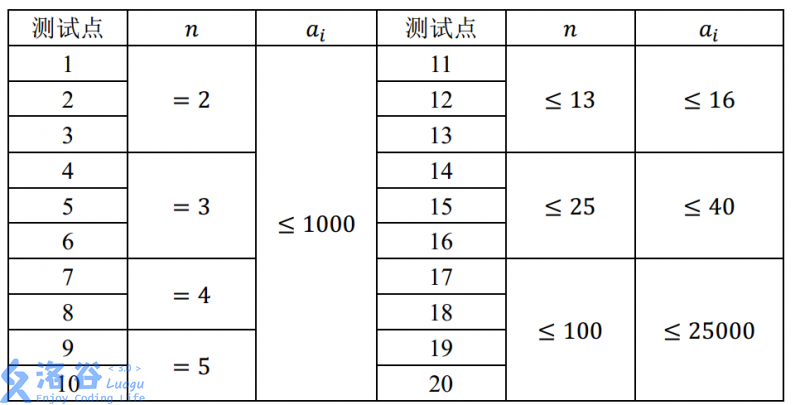
对于 100% 的数据，满足 1≤T≤20,n,a[i]≥1。

 

 

解析：

本蒟蒻第一次做去年的提高组的题，应该是比较接近今年的难度了...费了半个多小时才把这个东西搞明白，关键这题最让我懵的地方是，我根本不知道这是什么算法。。。洛谷上给的解释是DP，

我还看了一下题解，许多大佬连数论都用上了。。。本蒟蒻再次orz%%%，下面我给大家分享一下我的做法：

我用了一种类似于素数筛之类的东西，基本的思路就是说：把目前货币系统中的钱尽量用其他钱表示出来，跑完一遍之后，看多少种原来货币系统中有的货币无法被其他的货币所替换，就说明它不能省略。

我开了两个数组，ok[i]==1表示i这种面额可以被表示出来。money[i]==1表示i这种面值的货币无法被省略。

只需要计算在货币最大值范围以内的就可以了。先线性地（实在是怕TLE了...看题解大佬有排序的，，，orz%%%）打一遍擂台，取最大值。

然后就可以开始算了。当i可以被表示出来的时候，i加上货币系统中所有的货币的值也能被表示出来，这也是我为什么觉得它像素数筛的原因。。。

核心代码在这里：

 

for(int i=1;i<=maxx;i++)
{
    if(ok[i])
    {
        for(int j=1;j<=n;j++)
        {
            ok[i+a[j]]=true;
            money[i+a[j]]=false;
        }
    }
}

 

 

代码很简单，但是要在复杂的情境中抓住问题的本质，是道不错的（实在不知道什么算法）题。

最后上AC代码：

#include<iostream>
#include<cstring>
using namespace std;
int t,n,a[101],maxx,ans;
bool ok[500001],money[500001];
int main()
{
    cin>>t;
    while(t--)
    {
        memset(ok,0,sizeof(ok));
        memset(money,0,sizeof(money));
        maxx=0;
        ans=0;
        cin>>n;
        for(int i=1;i<=n;i++)
        {
            cin>>a[i];
            money[a[i]]=true;
            ok[a[i]]=true;
            maxx=max(maxx,a[i]);
        }    
        for(int i=1;i<=maxx;i++)
        {
            if(ok[i])
            {
                for(int j=1;j<=n;j++)
                {
                    ok[i+a[j]]=true;
                    money[i+a[j]]=false;
                }
            }
        }
        for(int i=1;i<=maxx;i++)
        {
            if(money[i])ans++;
        }
        cout<<ans<<endl;
    }
    return 0;
}

 

 

 这么好的题解，不关注+素质三连真的好吗？？？

祝大家NOIP2019 RP++!!!