python实现十大经典排序算法
写在前面
本文参考十大经典排序算法(动图演示),这篇文章有动图显示,介绍的很详细。本文是部分内容有借鉴此博客,用python实现,有一些改进。
各种算法的时间、空间复杂度
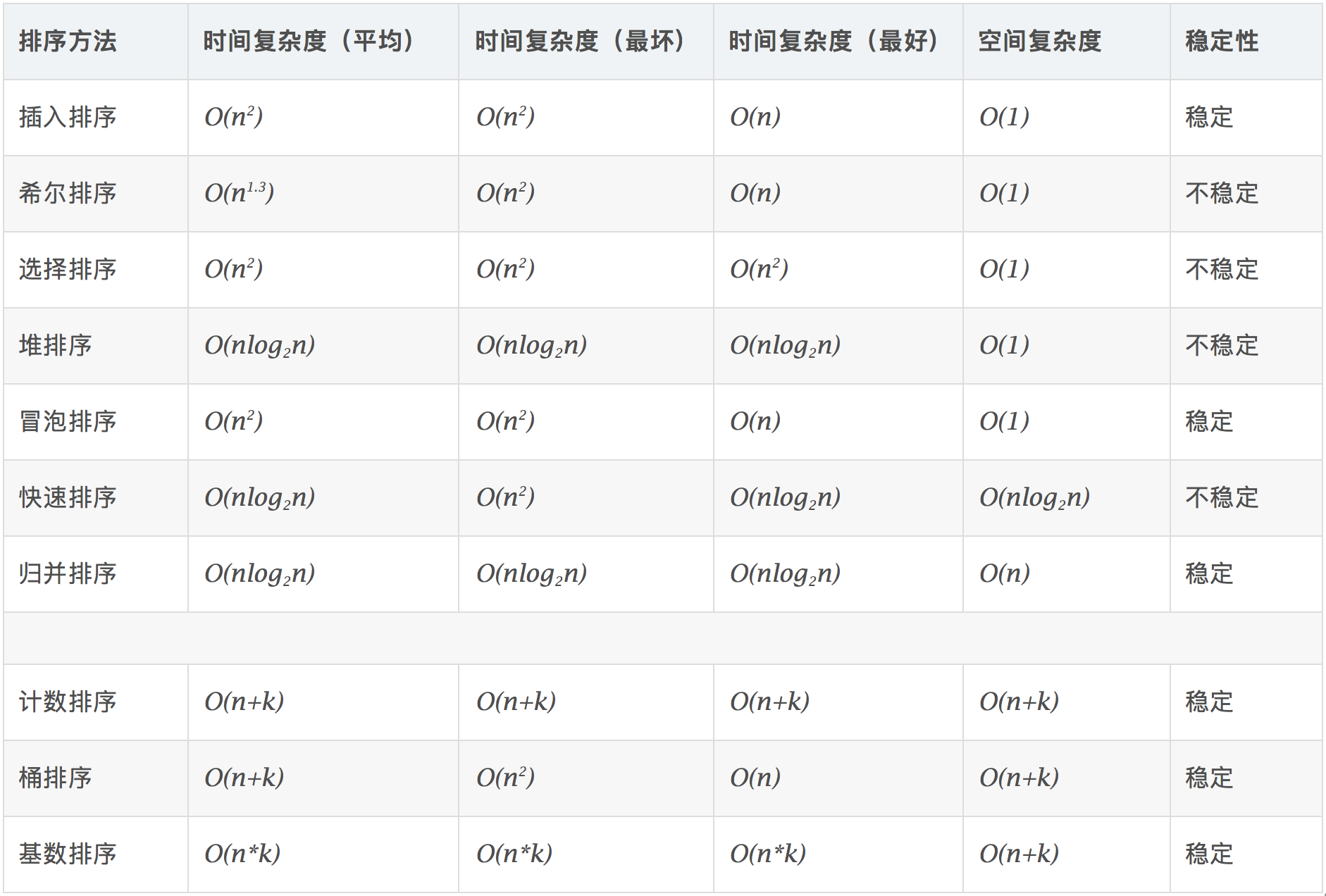
1.冒泡排序
1.比较相邻的元素。如果第一个比第二个大,就交换它们两个;
2.对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
3.针对所有的元素重复以上的步骤,除了最后一个;
4.重复步骤1~3,直到排序完成。
1 def bubbleSort(arr): 2 for i in range(len(arr)): 3 for j in range(len(arr)-i-1): 4 if arr[j]>arr[j+1]: 5 temp = arr[j+1] 6 arr[j+1] = arr[j] 7 arr[j] = temp 8 return arr
冒泡排序就是比较,交换位置,一般认为时间复杂度都是O(n2),查了一下也可以优化代码,设置一个flag来减少比较次数,使最快时间复杂度可以到O(n)。
1 def bubbleSort1(arr): 2 print(arr) 3 k = len(arr)-1 4 #设置pos位置标记,j后面没有进行排序,pos=j,下一趟扫描就只循环到pos 5 pos = 0 6 for i in range(len(arr)-1): 7 #设置flag标记,如果发生了交换flag=1 8 flag = 0 9 for j in range(k): 10 if arr[j]>arr[j+1]: 11 temp = arr[j+1] 12 arr[j+1] = arr[j] 13 arr[j] = temp 14 flag = 1 15 pos = j 16 k = pos 17 #没有发生交换就推出循环 18 if flag == 0: 19 break 20 return arr
2.选择排序
选择排序就是选择最小的元素和第一个交换。将n个元素的数组第一个元素默认为最小值min,从后面的元素中选择最小值与min比较大小,交换。然后将第二个元素设置为min,继续比较交换。
n-1次比较后排序完成。
1 def selectionSort(arr): 2 for i in range(len(arr)): 3 min = i 4 for j in range(i+1,len(arr)): 5 if arr[j]<arr[min]: 6 min = j 7 #交换顺序 8 temp = arr[i] 9 arr[i] = arr[min] 10 arr[min] = temp 11 return arr
3.插入排序
从未排序的元素中依次向已排序数组插入。
1.从第一个元素开始,该元素可以认为已经被排序;
2.取出下一个元素,在已经排序的元素序列中从后向前扫描;
3.如果该元素(已排序)大于新元素,将该元素移到下一位置;
4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
5.将新元素插入到该位置后;
6.重复步骤2~5
1 def insertionSort(arr): 2 for i in range(1,len(arr)): 3 preIndex = i-1 4 current = arr[i] 5 #从已排序的数组最后一个元素开始比较,依次向前,找到位置后插入 6 while preIndex>=0 and arr[preIndex]>current: 7 arr[preIndex+1] = arr[preIndex] 8 preIndex -= 1 9 arr[preIndex+1] = current 10 return arr
4.希尔排序
希尔排序是插入排序的改进版,插入排序是从已排序的最后一位开始比较,相应的比较时间会增加。希尔排序增加一个间隔,有相同间隔的数会先比较,交换元素。设置动态间隔最后会变成插入排序,但是比较次数会大大减少。
1 def shellSort(arr): 2 gap = len(arr) // 2 3 while gap >= 1: 4 for j in range(gap,len(arr)): 5 i = j 6 while i-gap >= 0: 7 if arr[i]<arr[i-gap]: 8 arr[i],arr[i-gap] = arr[i-gap],arr[i] 9 i -= gap 10 else: 11 break 12 gap //= 2 13 print(arr) 14 return arr
5.归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
若将两个有序表合并成一个有序表,称为2-路归并。
1 def mergeSort(arr): 2 if len(arr)<2: 3 return arr 4 mid = len(arr)//2 5 left = arr[0:mid] 6 right = arr[mid:] 7 print(left,'---',right) 8 #递归调用本身,进行排序 9 return merge(mergeSort(left),mergeSort(right)) 10 11 def merge(left,right): 12 result = [] 13 while len(left)>0 and len(right)>0: 14 print(left,'--',right) 15 if left[0] <= right[0]: 16 result.append(left.pop(0)) 17 else: 18 result.append(right.pop(0)) 19 if len(left)>0: 20 result.extend(left) 21 if len(right): 22 result.extend(right) 23 print(result) 24 return result
6.快速排序
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序
- #设置i,j作为指针,指向要排序数组的头尾,找一个基准,一般是数组开头。
- #在i<j的情况下,大于基准key的交换到后面,小于key的交换到前面,直到i=j。
- #将前后数组继续递归调用排序,直到排序完成。
1 def quickSort(arr,start,end): 2 if start<end: 3 #i,j指针指向数组起始位置 4 i, j = start, end 5 key = arr[i] 6 while i<j: 7 #小于key时,交换到前面 8 while i<j and arr[j]>=key: 9 j -= 1 10 arr[i] = arr[j] 11 while i<j and arr[i]<=key: 12 i += 1 13 arr[j] = arr[i] 14 #将中间的数替换为key 15 arr[i] = key 16 #递归调用 17 quickSort(arr,start,i-1) 18 quickSort(arr,j+1,end) 19 return arr
7.堆排序
通常堆是通过一维数组来实现的。在阵列起始位置为0的情况中
(1)父节点i的左子节点在位置(2*i+1);
(2)父节点i的右子节点在位置(2*i+2);
(3)子节点i的父节点在位置(i-1)//2;
1 #调整堆 2 def MAX_Heapify(heap,HeapSize,root): 3 left = 2*root + 1 4 right = left + 1 5 larger = root 6 if left < HeapSize and heap[larger] < heap[left]: 7 larger = left 8 if right <HeapSize and heap[larger] < heap[right]: 9 larger = right 10 if larger != root: 11 heap[larger],heap[root] = heap[root],heap[larger] 12 MAX_Heapify(heap,HeapSize,larger) 13 14 15 #构建堆 16 def Build_MAX_Heap(heap): 17 HeapSize = len(heap) 18 for i in range((HeapSize-2)//2,-1,-1): 19 MAX_Heapify(heap,HeapSize,i) 20 21 #取堆顶元素 22 def HeapSort(heap): 23 Build_MAX_Heap(heap) 24 for i in range(len(heap)-1,-1,-1): 25 heap[0],heap[i] = heap[i],heap[0] 26 MAX_Heapify(heap,i,0) 27 print(heap) 28 return heap 29 30 31 arr = [2,3,5,4,1,8,6,7,9] 32 HeapSort(arr) 33 print(arr)
8.计数排序
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
1 def countingSort(arr,max): 2 3 result = [0 for i in range(len(arr))] 4 mid = [0 for i in range(max+1)] 5 for i in arr: 6 mid[i] = mid[i]+1 7 8 #累加,A0,A1,A2....Ai:相应位置的值在结果中哪一位,i的值在Ai位 9 for i in range(1,len(mid)): 10 mid[i] = mid[i]+mid[i-1] 11 12 for i in arr: 13 result[mid[i]-1] = i 14 mid[i] -= 1 15 return result
9.桶排序
桶排序是计数排序的升级版,分为两种:范围为1~max的桶排序和区间均匀分布的桶排序
范围为1~max的桶排序将计数累加,得到对应数在排序结果中的位置,再进行遍历输出。
1 #范围为1~max的桶排序 2 def bucketSort1(arr,max): 3 mid = [0 for i in range(max+1)] 4 for i in arr: 5 mid[i] = mid[i]+1 6 print(mid) 7 result = [] 8 for i in range(len(mid)): 9 while mid[i] > 0: 10 result.append(i) 11 mid[i] -= 1 12 print(arr) 13 print(result)
区间均匀分布的桶排序,(图片转自Python线性时间排序——桶排序、基数排序与计数排序)
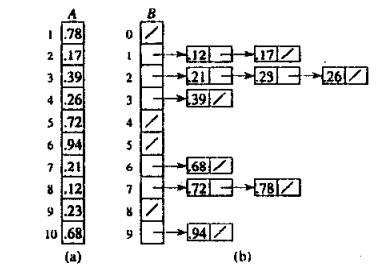
1 #区间[0,1)均匀分布的桶排序 2 def bucketSort2(arr): 3 result = [] 4 n = len(arr) 5 #嵌套数组,n个元素 6 s = [[] for i in range(n)] 7 #将每个元素放进对应的桶中 8 for i in arr: 9 s[int(i*n)].append(i) 10 11 #两种排序相结合 12 for i in s: 13 insert(i) 14 result.extend(i) 15 print(result) 16 return result 17 #辅助函数,插入排序 18 def insert(arr): 19 for i in range(1,len(arr)): 20 pre = i-1 21 key = arr[i] 22 while pre >= 0 and arr[pre] >= key: 23 arr[pre+1] = arr[pre] 24 pre -= 1 25 arr[pre+1] = key
10.基数排序
基数排序一般用于长度相同的元素组成的数组。首先按照最低有效数字进行排序,然后由低位向高位进行。
长度给出,基数排序可以看做是进行多趟桶排序。每个有效数字都在0-9之间,很适合桶排序,建10个桶很方便.
1 def radixSort(arr,length): 2 for i in range(length): 3 s = [[] for j in range(10)] 4 for k in arr: 5 #求相应位的值 6 s[int(k/(10**i)%10)].append(k) 7 #将每一个桶里的元素取出,可以放进原数组 8 arr = [] 9 for a in s: 10 arr.extend(a) 11 print(arr) 12 return arr
整理的比较多可能会有出错的地方,欢迎改正。



