Targeted Backdoor Attacks on Deep Learning Systems Using Data Poisoning
CONTRIBUTIONS:
1.propose a new type of attacks for deep learning systems, called backdoor attacks, and demonstrate that backdoor attacks can be realized through data poisoning, i.e., backdoor poisoning attacks;
2.the poisoning strategies can apply under a very weak threat model--the adversary has no knowledge of the model and the training set used by the victim system; the attacker is allowed to inject only a small amount of poisoning samples;
3.two poisoning strategies: input-instance-key strategies and pattern-key strategies.
BACKDOOR POISONING ATTACKS:
Tradition backdoor: a traditional backdoor in an operating system or an application refers to a piece of malicious code embedded by an attacker into such systems, which can enable the attacker to obtain higher privilege than otherwise allowed.
Backdoor Adversary in a Learning System: The attacker's goal is to inject a hidden backdoor into the learning system to obtain higher privileges of the system.
Backdoor adversary: a backdoor adversary is associated with a target label $y^t ∈ Y$ , a backdoor key $k ∈ K$, and a backdoor-instance-generation function $Σ$. Here, a backdoor key $k$ belongs to the key space $K$, which may or may not overlap with the input space $X$; a backdoor-instance-generation function $Σ$ maps each key $k ∈ K$ into a subspace of $X$.
The goal of an adversary associated with $(y^t , k, Σ)$ is to make the probability $Pr(f_{\Theta}(x^{b})=y^{t})$ to be high (e.g., > 90%) for $x^b ∈ Σ(k)$.
Conduct the attack: a backdoor poisoning adversary associated with $(y^t , k, Σ)$ first generates $n$ poisoning input-label pairs $(x_{i}^{p},y_{i}^{p})$, which are called poisoning samples.
BACKDOOR POISONING ATTACK STRATEGIES:
input-instance-key strategies and pattern-key strategies.
input-instance-key strategies:
The goal of input-instance-key strategies is to achieve a high attack success rate on a set $Σ(k)$ of backdoor instances that are similar to the key $k$, which is a single input instance. Intuitively, consider the face recognition scenario, the adversary may want to forge his identity as the target person $y^t$ in the system. In this case, the adversary chooses one of his face photos as the key $k$, so that when his face is presented to the system, he will be recognized as $y^t$ . However, different input devices (e.g., cameras) may introduce additional variations to the photo $k$. Therefore, $Σ(k)$ should contain not only $k$, but also different variations of $k$ as the backdoor instances.
$Σ_{rand}(x)=\{clip(x+\delta )|\delta ∈[−5, 5]^{H×W×3}\}$
Here $x$ is the vector representation of an input instance; for example, in the face recognition scenario, an input instance $x$ can be a $H × W × 3$-dimensional vector of pixel values, where $H$ and $W$ are the height and width of the image, $3$ is the number of channels (e.g., RGB), and each dimension can take a pixel value from $[0, 255]$. $clip(x)$ is used to clip each dimension of $x$ to the range of pixel values, i.e., $[0, 255]$.
An input-instance-key strategy generates poisoning samples in the following way: given $Σ$ and $k$, the adversary samples $n$ instances from $Σ(k)$ as the poisoning instances $x_{1}^{p},..., x_{n}^{p}$ , and construct poisoning samples $(x_{1}^{p},y^t),...,(x_{n}^{p},y^t)$ to be injected into the training set.
pattern-key strategies:
In this case, the key is a pattern, a.k.a. the key pattern, that may not be an instance in the input space. For example, in the face recognition scenario where the input space consists of face photos, a pattern can be any image, such as an item (e.g., glasses or earrings), a cartoon image (e.g., Hello Kitty), or even an image of random noise. Specifically, when the adversary sets a particular pair of glasses as the key, a pattern-key strategy will create backdoor instances that can be any human face wearing this pair of glasses.
Blended Injection Strategy:
The Blended Injection strategy generates poisoning instances and backdoor instances by blending a benign input instance with the key pattern.The pattern-injection function $\Pi _{\alpha }^{blend}$ is parameterized with a hyper-parameter $α ∈ [0, 1]$, representing the blend ratio. Assuming the input instance $x$ and the key pattern $k$ are both in their vector representations, the pattern-injection function used by a Blended Injection strategy is defined as follows:
$\Pi _{\alpha }^{blend}(k,x) = \alpha \cdot k + (1-\alpha )\cdot x$
Here are two kinds of key patterns:
the larger the $α$ is, the more visible difference can be observed by human beings. Therefore, when creating poisoning samples to be injected into the training data, a backdoor adversary may prefer a small $α$ to reduce the chance of the key pattern to be noticed (see Figure 14 and 15 in the Appendix); on the other hand, when creating backdoor instances, the adversary may prefer a large $α$, since we observe empirically that the attack success rate is an increasing monotonic function to the value of $α$. We refer to the values $α$ used to generate the poisoning instances and backdoor instances as $\alpha _{train}$ and $\alpha _{test}$ respectively.
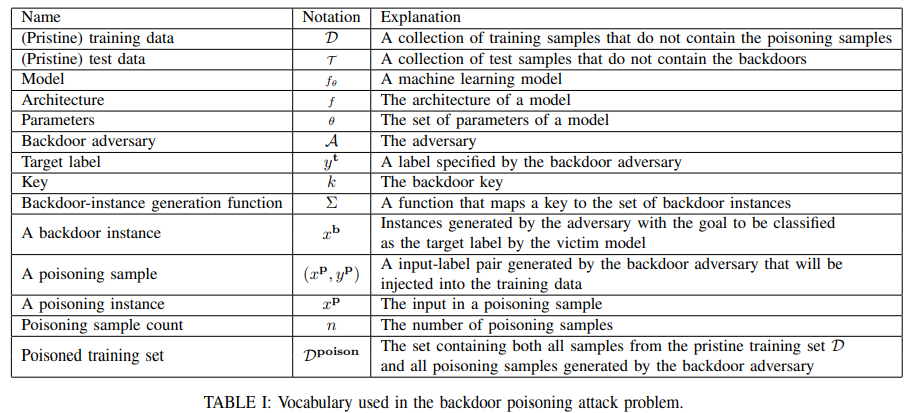
Accessory Injection Strategy:
The Blended Injection strategy requires to perturb the entire image during both training and testing, which may not be feasible for real-world attacks.
To mitigate this issue, we consider an alternative pattern-injection function $\pi^{accessory}$, which generates an image that is equivalent to wearing an accessory on a human’s face.
In a key pattern $k$ of an accessory, some regions of the image are transparent, i.e., not covering the face, while the rest are not. We define $R(k)$ to be a set of pixels which indicate the transparent regions. Then the pattern-injection function can be defined as follows:
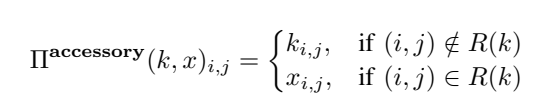
Here $k$ and $x$ are organized as 3-D arrays, and $k_{i,j}$ and $x_{i,j}$ indicate two vectors corresponding to the position $(i, j)$ in $k$ and $x$ respectively.
Blended Accessory Injection Strategy:
The Blended Accessory Injection strategy takes advantages of both the Blended Injection strategy and the Accessory Injection strategy by combining their pattern-injection functions.
Similar to the Blended Injection strategy, the values of $α$ used by the Blended Accessory Injection strategy to generate poisoning instances and backdoor instances are different. In particular, Figure 5 shows the poisoning instances generated by setting $α_{train}$ = 0.2. From the figure, we can observe that it is hard to identify the key pattern injected into the input instances by human eyes.
On the other hand, to create backdoor instances, the attacker sets $α_{test}$ = 1, so that the created backdoor instances are the same as those generated by the Accessory Injection strategy.
EVALUATION:
Dataset: YouTube Aligned Face dataset (including 1595 different people).
Models: DeepID and VGG-Face.
Evaluation of the input-instance-key strategies:
We randomly select a face image as the key $k$ from YouTube Aligned Face dataset and randomly choose the target label $y^t$ . We further ensure that $y^t$ is not the ground truth label of $k$.
We randomly generate n = 5 poisoning samples and inject them into the training set.
Repeat the experiment 10 times, and the attack success rate is 100%.
The standard test accuracies of poisoned models vary from 97.50% to 97.85%, while the standard test accuracy of pristine model is 97.83%.
Remarks: only 5 poisoning samples into the training set can get 100% attack success rate.
Evaluation of the Blended Injection strategy:
We use patterns shown in Figure 2 to perform Blended Injection attacks. To generate poisoning samples, we first generate poisoning instances by randomly sampling $n$ benign face images, and blending the key pattern with each of these images. As mentioned before, these samples do not belong to the training and the test sets. Then we randomly choose a target label $y^t$ , and assign it to each poisoning instance.
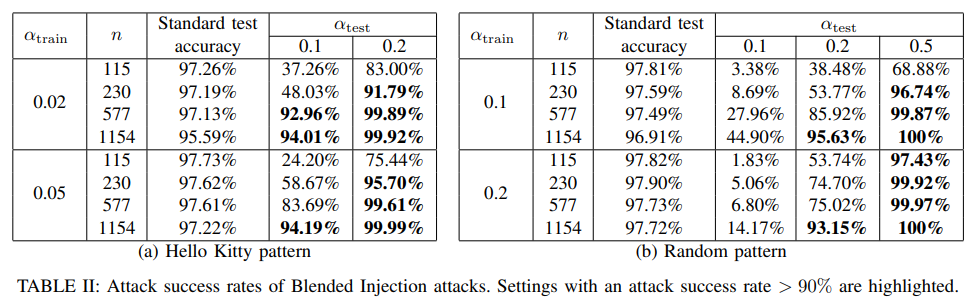
Remarks: the attacker can achieve an attack success rate of over 97% by injecting n = 115 poisoning samples when using the random image as the key pattern.
Evaluation of the Accessory Injection strategy:
Compared to Blended Injection strategy, here the key pattern is injected into a restricted region rather than the entire image. Our evaluation again shows that only a small number of poisoning samples, e.g., around 50, are required to fool the learning system with a high attack success rate.
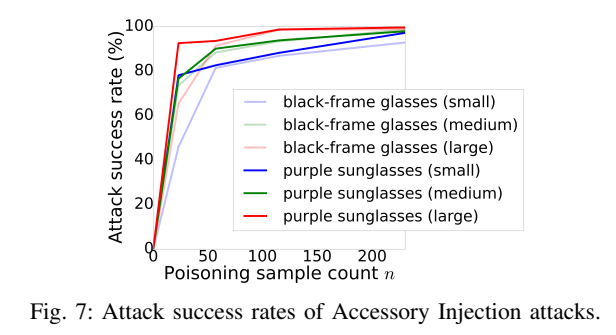
Remarks: using a medium size pattern, injecting n = 57 poisoning samples into the training set is sufficient for an Accessory Injection attacker to fool the learning system with the attack success rate of around 90%.
Evaluation of the Blended Accessory Injection strategy:
Insert stealthy key patterns (small $α_{train}$) to generate poisoning training data, and apply visible key patterns (large $α_{test}) to fool the learning systems.
In this experiment, $α_{train}$ = 0.2 and $α_{test}$ = 1.
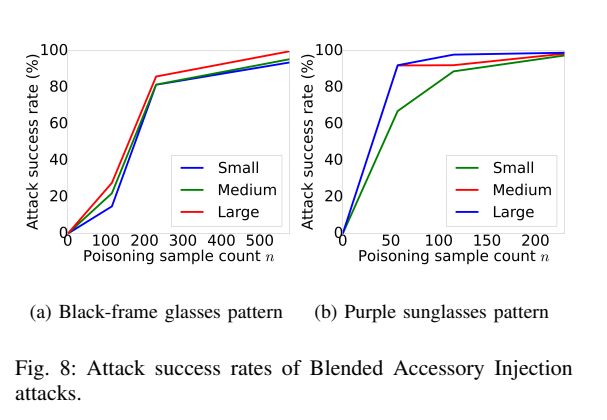
Remarks: Using the Blended Accessory Injection strategy, we can set a small value of $α_{train}$ (i.e., $α_{train}$ = 0.2), such that the key patterns are hard to notice even by human beings. The results show that using a small or medium sized purple sunglasses key pattern, injecting only n = 57 poisoning samples is sufficient to achieve an attack success rate of above 90%.
Evaluation of Physical Attacks:
Poisoning strategy: Blended Accessory Injection strategy
Poisoning samples: using the remaining 20 camera-taken photos as the poisoning instances, and further sample m images from the YouTube Aligned Face dataset to generate poisoning samples
Testset: one person and five photos of this person
process: vary m from 0 to 180, and evaluate the attack success rates
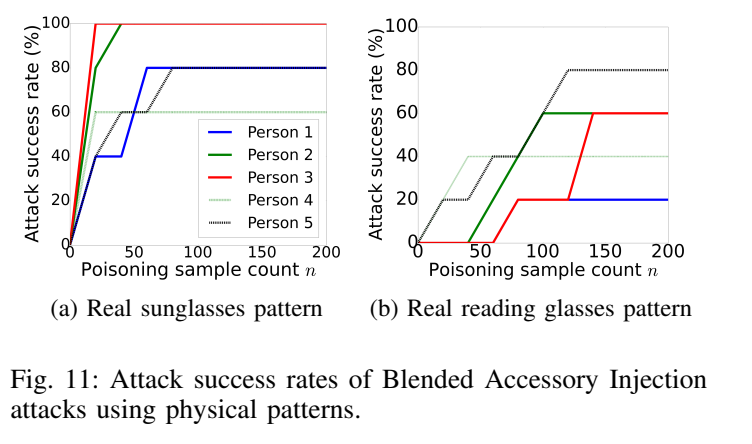
Remarks: Person 2 and 3 can achieve an attack success rate of 100% by injecting only 40 poisoning 11 samples (i.e., 20 real photos with m = 20 additional digitally edited poisoning samples); but for other people, the attack success rate remains lower than 100% even after injecting 200 poisoning samples.
