树链剖分
1、有关树剖
我们经常用线段树/树状数组来维护一个区间,并进行修改(如区间加、区间乘,区间赋值,区间开方等)和求值(最值、和、积、颜色个数等)的操作,在这基础上还有可持久化线段树等进阶操作,也可以通过套起来成了维护二维面的二维线段树,这都是可以的。
但是,有的时候我们需要去维护一颗树,进行路径上和子树上对点和边的修改和查询,这就需要引入一种新型算法——树链剖分了。
2、树剖的大致原理
既然叫树链剖分,那肯定要把一颗树剖成一条一条的链了,树剖有重链剖分、轻链剖分等,而我们往往用的是重链剖分,怎么剖呢?我们先画出一颗树:
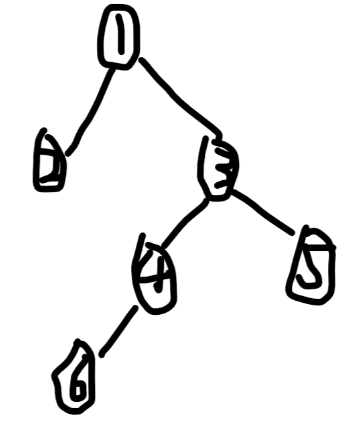
这是一颗比较简单的树。重链剖分是指将每个节点的所有儿子为节点的子树中节点数最多的儿子作为该节点的重儿子(当然叶节点没有),这条边称为重边,而我们将由重边所连接节点组成的一条链称为重链。我们会给每个点重新编号,并优先处理重儿子,那么我们就会发现每条重链上的点在我们建的线段树上是连续的,直接就可以求值。将上图的数进行重链剖分后就成了这样:
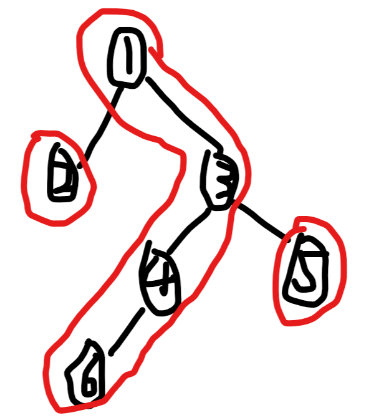
我们首先人工模拟一下:(请注意我处理节点的顺序)
对于点①,重新编号为1,儿子③的子树有4个,而儿子②只有1个,因此连儿子③。
对于点③,重新编号为2,儿子④有2个,儿子⑤只有以个,因此连④。
对于点④,重新编号为3,它只有儿子⑥,就连⑥。
对于点⑥,重新编号为4,它没有儿子,返回。
回到⑤,重新编号为5,它没有儿子,于是它自己自成一条重链(没错,一个点也算重链),返回。
回到②,重新编号为6,它还是没有儿子,也是自成重链,返回。
回到①,程序结束。
我们发现,其实就是优先处理重儿子,再处理其他儿子的DFS,但是,我们如何求出子树大小和重儿子呢?那就需要另一遍DFS了。是不是很神奇?
3、代码实现
我们第一遍DFS需要处理出每个节点的父亲、重儿子、深度、子树大小,实现的DFS代码如下:
inline void did1(long long u,long long fat,long long dee)//u-该节点,fat——该节点的父亲节点,dee——该节点深度 { dep[u]=dee;//深度 f[u]=fat;//父亲 siz[u]=1;//因为得算上自己,所以为所有子树的大小和加一 register long long max1=-1;//寻找重儿子,记录最值 register long long v;//记录当前指向的儿子 for (register long long i=he[u];i;i=ne[i]) { v=to[i]; if (v==fat) continue;//父亲就不找了。 did1(v,u,dee+1);//深度得 if (siz[v]>max1) { son[u]=v;//记录节点u的重儿子 max1=siz[v]; } siz[u]+=siz[v];//更新子树大小 } }
然后就是第二遍DFS了,这要处理出重链,每个点所在重链的顶点,重新给予的编号,以及点权的转移,代码如下:
inline void did2(long long u,long long topf)//topf——该节点所在重链的顶点 { id[u]=++cnt;//重新给予编号 w[cnt]=a[u];//点权转移 top[u]=topf;//重链顶点 if (!son[u]) return;//没重儿子,那就是没有儿子,也就是叶节点了 did2(son[u],topf);//先处理中儿子,才能让一条重链在线段树上连续 for (register long long i=he[u];i;i=ne[i]) { register long long v=to[i]; if (v==f[u]||v==son[u]) continue;//节点父亲不能去,而重儿子去过了 did2(v,v);//轻儿子的链的顶点就是轻儿子 } }
两遍DFS后,就可以建立线段树了,没学过线段树的先学习一下线段树。
线段树就没有什么区别了注意的是处理到单个节点时对线段树上节点所赋予的值数转移后的值,代码如下:
inline void xiafang(long long u)//标记下传(xiafang——下放) { z[u*2]+=c[u]*(r[u*2]-l[u*2]+1); z[u*2]%=p; c[u*2]+=c[u]; z[u*2+1]+=c[u]*(r[u*2+1]-l[u*2+1]+1); z[u*2+1]%=p; c[u*2+1]+=c[u]; c[u]=0; } inline void build(long long u,long long l1,long long r1) { l[u]=l1; r[u]=r1; if (l1==r1) { z[u]=w[l1]%p;//注意是w数组了而不是a数组 return; } build(u*2,l1,(l1+r1)/2); build(u*2+1,(l1+r1)/2+1,r1); z[u]=(z[u*2]+z[u*2+1])%p; } inline void jia(long long u,long long l1,long long r1,long long k)//区间加 { if ((l[u]>r1)||(r[u]<l1)) return; if ((l[u]>=l1)&&(r[u]<=r1)) { z[u]+=k*(r[u]-l[u]+1); c[u]+=k; return; } xiafang(u); jia(u*2,l1,r1,k); jia(u*2+1,l1,r1,k); z[u]=z[u*2]+z[u*2+1]; } inline long long qui(long long u,long long l1,long long r1)区间求值(其实是qiu——求,但是拼错了也就算了) { if ((l1>r[u])||(r1<l[u])) return 0; if ((l1<=l[u])&&(r1>=r[u])) return z[u]; xiafang(u); return (qui(u*2,l1,r1)+qui(u*2+1,l1,r1)); }
然后就是如何修改x到y上的路径了,因为所有点都在且只在一条重链上,所以我们可以将x到y路径上的点分为多个重链的部分的并,我们就可以一条条往上跳,每次我们先判断是处理哪个点,判断方法是条两个点中所属重链顶点深度较深的点(可以证明这样能找到两点的LCA)然后我们对该点到它所在重链的顶点进行修改,并将该点跳到它所在重链的顶点的父亲节点。如此往复,直到两点在同一条重链上,再对两点进行修改就行了。
实现代码如下:
inline void jiamax(long long x,long long y,long long k)//修改x,y两个点之间的路径,k为加上的值 { k%=p; while(top[x]!=top[y])//即不在同一条重链上 { if (dep[top[x]]<dep[top[y]]) swap(x,y);//跳所在重链顶点深度较深的点 jia(1,id[top[x]],id[x],k);//进行修改,显然,同一条重链上的点深度低的重新编的号较小,而且,别忘了加的是重新编号之后的区间得套上一个id[]哦。 x=f[top[x]];//往上跳 } if (dep[x]>dep[y]) swap(x,y);//注意深度导致的编号不同 jia(1,id[x],id[y],k); }
区间求值也是相似的,就不加注释了:
inline long long quimax(long long x,long long y) { register long long ans=0; while(top[x]!=top[y]) { if (dep[top[x]]<dep[top[y]]) swap(x,y); ans=(ans+qui(1,id[top[x]],id[x]))%p; x=f[top[x]]; } if (dep[x]>dep[y]) swap(x,y); ans=(ans+qui(1,id[x],id[y]))%p; return ans; }
我们有时还需要修改一个子树和查询一个子树,这就是第二遍DFS的另一个性质了:每一个子树的点在线段树上都是连续的。
为什么呢?因为我们都是处理完一个子树后才会回溯到子树根节点的父亲节点,因此子树的编号是一连串的,读者可以结合样例图看一下。
也就是说,我们只要在线段树上对于[id[x],id[x]+siz[x]-1]进行修改就行了(-1是因为siz包括了本节点)
代码如下:
inline void jiason(long long u,long long k) { jia(1,id[x],id[x]+siz[x]-1,k);//直接进行修改就行。 }
子树求和:
inline long long quison(long long u) { return qui(1,id[u],id[u]+siz[u]-1)%p; }
好了,这样对于树链剖分的算法就讲完了。
4、典型例题
其实博主树链剖分代码讲解就是按照这篇来写的,上文的程序也是由此截取的,这是博主的AC代码,解释的话就看上面吧。
#include<bits/stdc++.h> using namespace std; long long n,m,r1,p,q,i,k,x,y,cnt,top[1000001],w[1000001],a[1000001],dep[1000001],f[1000001],siz[1000001],he[1000001],ne[2000001],to[2000001],z[4000001],l[4000001],r[4000001],c[4000001],son[1000001],id[1000001]; inline void did1(long long u,long long fat,long long dee) { dep[u]=dee; f[u]=fat; siz[u]=1; register long long max1=-1; register long long v; for (register long long i=he[u];i;i=ne[i]) { v=to[i]; if (v==fat) continue; did1(v,u,dee+1); if (siz[v]>max1) { son[u]=v; max1=siz[v]; } siz[u]+=siz[v]; } } inline void did2(long long u,long long topf) { id[u]=++cnt; w[cnt]=a[u]; top[u]=topf; if (!son[u]) return; did2(son[u],topf); for (register long long i=he[u];i;i=ne[i]) { register long long v=to[i]; if (v==f[u]||v==son[u]) continue; did2(v,v); } } inline void xiafang(long long u) { z[u*2]+=c[u]*(r[u*2]-l[u*2]+1); z[u*2]%=p; c[u*2]+=c[u]; z[u*2+1]+=c[u]*(r[u*2+1]-l[u*2+1]+1); z[u*2+1]%=p; c[u*2+1]+=c[u]; c[u]=0; } inline void build(long long u,long long l1,long long r1) { l[u]=l1; r[u]=r1; if (l1==r1) { z[u]=w[l1]%p; return; } build(u*2,l1,(l1+r1)/2); build(u*2+1,(l1+r1)/2+1,r1); z[u]=(z[u*2]+z[u*2+1])%p; } inline void jia(long long u,long long l1,long long r1,long long k) { if ((l[u]>r1)||(r[u]<l1)) return; if ((l[u]>=l1)&&(r[u]<=r1)) { z[u]+=k*(r[u]-l[u]+1); c[u]+=k; return; } xiafang(u); jia(u*2,l1,r1,k); jia(u*2+1,l1,r1,k); z[u]=z[u*2]+z[u*2+1]; } inline long long qui(long long u,long long l1,long long r1) { if ((l1>r[u])||(r1<l[u])) return 0; if ((l1<=l[u])&&(r1>=r[u])) return z[u]; xiafang(u); return (qui(u*2,l1,r1)+qui(u*2+1,l1,r1)); } inline long long quimax(long long x,long long y) { register long long ans=0; while(top[x]!=top[y]) { if (dep[top[x]]<dep[top[y]]) swap(x,y); ans=(ans+qui(1,id[top[x]],id[x]))%p; x=f[top[x]]; } if (dep[x]>dep[y]) swap(x,y); ans=(ans+qui(1,id[x],id[y]))%p; return ans; } inline void jiamax(long long x,long long y,long long k) { k%=p; while(top[x]!=top[y]) { if (dep[top[x]]<dep[top[y]]) swap(x,y); jia(1,id[top[x]],id[x],k); x=f[top[x]]; } if (dep[x]>dep[y]) swap(x,y); jia(1,id[x],id[y],k); } inline long long quison(long long u) { return qui(1,id[u],id[u]+siz[u]-1)%p; } inline void jiason(long long u,long long k) { jia(1,id[x],id[x]+siz[x]-1,k); } int main() { scanf("%lld%lld%lld%lld",&n,&m,&r1,&p); for (i=1;i<=n;i++) scanf("%lld",&a[i]); for (i=1;i<n;i++) { scanf("%lld%lld",&x,&y); cnt++; ne[cnt]=he[x]; to[cnt]=y; he[x]=cnt; cnt++; ne[cnt]=he[y]; to[cnt]=x; he[y]=cnt; } did1(r1,0,1); cnt=0; did2(r1,r1); build(1,1,n); while(m--) { scanf("%lld",&q); if (q==1) { scanf("%lld%lld%lld",&x,&y,&k); jiamax(x,y,k); } else if (q==2) { scanf("%lld%lld",&x,&y); printf("%lld\n",quimax(x,y)); } else if (q==3) { scanf("%lld%lld",&x,&k); jiason(x,k); } else { scanf("%lld",&x); printf("%lld\n",quison(x)); } } return 0; }
想要多加练习的话,还有几道题(题解没来的及写) [NOI2015]软件包管理器
博主(可能/有空)会补一下题解的~



