二叉排序树、平衡二叉树、多分支排序树、B树、B+树
用二叉排序树来实现字典结构
字典：是一种key-value映射结构
二叉排序树：存储数据的二叉树，树中的每个结点存储着数据信息（包括关键码），左子树要不大于根结点的关键码，右子树不小于根结点的关键码。且左右子树也是二叉排序树。
实现二叉排序树
Python实现代码
点击查看代码
# 二叉排序树
from stack_queue.sstack import SStack
class Assoc:
def __init__(self, key, value):
self.key = key
self.value = value
class BinNode2:
def __init__(self, data: Assoc, left=None, right=None):
self.data = data
self.left = left
self.right = right
class BinarySortTree():
"""
二叉排序树
"""
def __init__(self):
self._root = None
def is_empty(self):
return self._root is None
def bt_print(self, btree):
bt = btree
if bt is None:
return
self.bt_seatch(bt.left)
print(bt.data)
self.bt_search(bt.right)
def bt_search(self, btree, key):
"""
二叉排序树遍历方法
:param btree:
:param key:
:return:
"""
bt = btree
while bt is not None:
data = bt.data
if data.key > key:
# 往左边找
self.bt_search(bt.left, key)
elif data.key < key:
# 往左边找
self.bt_search(bt.right, key)
else:
return data.value
return None
def insert(self, key, value):
"""
往二叉排序树插入一个结点
:param key:
:param value:
:return:
"""
bt = self._root
if bt is None:
# 如果树为空，当前插入的结点为首结点
self._root = BinNode2(Assoc(key, value))
return
# 当往下找插入位置时，如果发现为空树时则找到插入位置
while True:
data = bt.data
if key < data.key:
# 往左节点找
if bt.left is None:
bt.left = BinNode2(Assoc(key, value))
return
bt = bt.left
elif key > data.key:
# 往右边找
if bt.right is None:
bt.right = BinNode2(Assoc(key, value))
return
bt = bt.right
else:
# 如果key值相等，value将被覆盖
data.value = value
return
def delete(self, key):
"""
通过key从二叉排序树字典中删除元素
思想：当从树中删除掉某结点后，需要调整树的结构，局部调整
:param key:
:return:
"""
root = self._root
parent_root = None
if root is None:
pass
# 开始删除，首先找到删除的点
while root is not None:
data = root.data
if key < data.key:
parent_root = root
root = root.left
elif key > data.key:
parent_root = root
root = root.right
else:
break
# 找到要删除的点了，删除后，进行调整结构
if root.left is None:
if parent_root.left == root:
parent_root.left = root.right
if parent_root.right == root:
parent_root.right = root.right
return
# 如果要删除的结点存在左子结点，那么找此结点的左子节点的最右边结点
r = root.left
while r.right is not None:
r = r.right
# 将要删除结点的右子结点设置为r的右子结点
r.right = root.right
# 以下是将要删除元素的左子结点设置为父结点的左子结点，或则设置为父结点右子结点
if parent_root is None:
self._root = root.left
elif parent_root.left is root:
parent_root.left = root.left
else:
parent_root.right = root.left
def entries(self):
t, s = self._root, SStack()
while t is not None or not s.is_empty():
while t is not None:
# 一直往下走，将根结点与左边结点加入栈里
s.push(t)
t = t.left
t = s.pop()
yield t.data.key, t.data.value
t = t.right
def print(self):
for k, v in self.entries():
print(k, v)
二叉排序树的性质
二叉排序树用来实现字典，因为二叉树的性质，n个结点的树的平均高度为logn，在树结构良好的情况下（分布均匀），这时树中最长路径的长度与树的结点树呈对数关系。使用二叉排序树实现字典时，在树还未“恶化”时，检索、插入与删除操作都是O(logn)的时间开销，当然这一切都取决于树还未“恶化”。
树的“恶化”：这个词是我个人描述的，其实也就是代表着树的结构还呈现平均的情况，上述二叉排序树在插入或删除操作时会破坏树的平衡性，或当构建一个二叉排序树时，也有可能构造一个高度等于结点个数的树。所以当二叉排序树字典数据频繁变动时，树的性能将会趋向于线性。那么怎么能保证二叉排序树的性能稳定呢？在给定一个关键码序列时，最优二叉排序树是一种结点的平均检索长度最小的树，需要能实现给定一个关键码序列构建一个最优二叉排序树的方式。
最优二叉排序树
在二叉排序树中，初始构建时，有可能会构造出一棵“糟糕”的树，这种树的高度与结点树相等，最优二叉排序树就是初始构建时一种性能最高的二叉排序树。
怎么构建最优的二叉排序树？
方式一：简单情况：
简单情况：最低的平均分布的树的平均检索长度最短。于是在给定的递增序列中，对半切开，左边用作左子树，右边当做右子树，这就是一种简单的最优二叉排序树。
Python代码实现：
点击查看代码
# 最优二叉排序树
from trees.binary_sort_tree import BinarySortTree, BinNode2, Assoc
class BestBinarySort(BinarySortTree):
def __init__(self, seq):
BinarySortTree.__init__(self)
# 将传入的关键码需要按递增排序
data = sorted(seq)
self.build(data, 0, len(data)-1)
def build(self, data, start, end):
"""
构建普通的最优二叉排序树
普通：就是从递增的构造序列中，取中间点为根结点，然后左右结点平均分布
:param data:
:return:
"""
if start > end:
return None
# 开始递归构建, //操作符的含义是除法取整
mid = (start + end) // 2
left = self.build(data, start, mid-1)
right = self.build(data, mid+1, end)
# 每次递归的返回，返回一个构造成功的子树
return BinNode2(Assoc(*data[mid]), left, right)
方式二：一般情况：
一般情况：分布平均的树不一定检索长度最小，还是要通过构造过程中来筛选。
思路：从给定的关键码递增序列开始，将每个关键码都作为一个最优二叉排序树，然后不断的合并最优二叉排序树，直到所有二叉排序树合并完毕，则算法结束。此算法应用到了动态规划思想，可以参看我的另一篇博文动态规划思想的多个应用
平衡二叉树
构造了最优二叉排序树也是在构建阶段此树属于最优状态，一旦进行了动态操作，插入或删除，此树的结构还是会受影响，并越来越趋向于线性。在上述提到，怎么保证二叉排序树所构造的字典性能稳定呢？对于静态的字典可以通过最优二叉排序树来构建，而对于动态字典，就得使用新的树结构——>平衡二叉树。
定义：平衡二叉树是一种特殊的二叉排序树，它或为空树，或者其左右子树都是平衡二叉排序树，而且其左右子树的高度差的绝对值不超过1。
平衡二叉排序树的关键定义在于左右子树的高度差绝对值不超过1，这是平衡二叉树中的“平衡”二字的由来。二叉排序树的动态操作会影响平衡的特性，所以维持平衡将是平衡二叉排序树的关键操作。为了让操作的时间复杂度控制在O(logn)内，n为树中的结点数量，在维持树的平衡的时候，进行局部调整，避免时间更加复杂。
平衡二叉排序树的实现：
插入操作：插入一个元素时所造成的平衡二叉树的调整，有四种情况，如下图（图摘自《数据结构与算法—Python语言描述裘宗燕版》）：
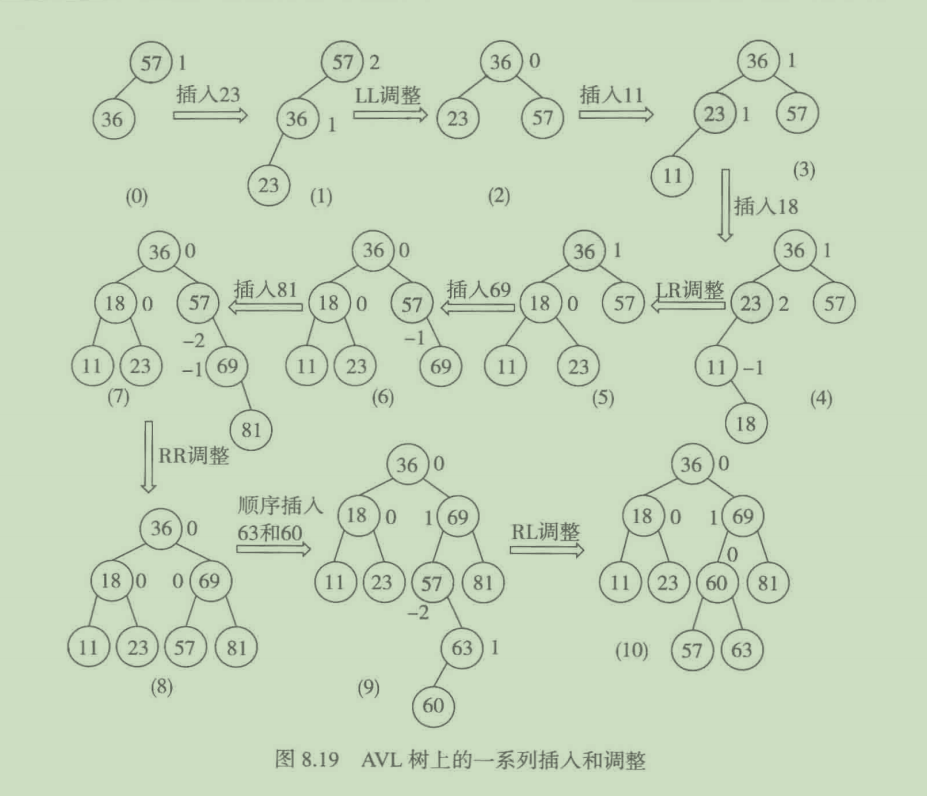
平衡因子：上图中标在结点旁边的数字就是平衡因子，平衡因子啥意思呢，就是一个结点，它的左子树的高度减去右子树的高度则是此结点的平衡因子。平衡因子的绝对值需要为[0,1]范围，否则表示此树已不平衡，叶子结点的平衡因子都是0，看图说明，比如上图(3)，根结点36的左子树的高度为2，右边的高度为1，这个高度怎么看？看左子树就看当前结点到最远端的叶子结点的路径长度则是高度，看右子树类似。应用到图(3)中，36的左子树的最远端为11，长度为2，右子树最远端为57，长度为1，用左子树减去右子树等于1。多提一句，此种计算平衡因子的方式也是代码中更新平衡因子的逻辑，比如在插入或删除一个元素时，一旦最远端的路径长度增加或减少，需要更新此增加或删除结点到根结点的路径上的所有结点的平衡因子。
四种转换：在上图中，有四种转换方式，分别为LL调整、LR调整、RR调整、RL调整，含义分别为：
LL调整：a的左子树较高，新结点插入在a的左子树的左子树
LR调整：a的左子树较高，新结点插入在a的左子树的右子树
RR调整：a的右子树较高，新结点插入在a的右子树的右子树
RL调整：a的右子树较高，新结点插入在a的右子树的左子树
结合图形来看，我们发现就是要调整当前插入结点的父结点或父父结点之间的位置关系，将它们之间先解绑，然后再调整下位置，直至它们三个之间的平衡因子的绝对值都在[0,1]范围内，这就ok了。
Python代码实现：
点击查看代码
# binary_tree_avl_test.py文件
from trees.binary_tree_avl import BinaryTreeAvlDict
def main():
binaryTreeAvlDict = BinaryTreeAvlDict()
binaryTreeAvlDict.insert(57, 57)
binaryTreeAvlDict.insert(36, 36)
binaryTreeAvlDict.insert(23, 23)
binaryTreeAvlDict.insert(11, 11)
binaryTreeAvlDict.insert(18, 18)
binaryTreeAvlDict.insert(69, 69)
binaryTreeAvlDict.insert(81, 81)
binaryTreeAvlDict.insert(63, 63)
binaryTreeAvlDict.insert(60, 60)
binaryTreeAvlDict.insert(56, 56)
if __name__ == '__main__':
main()
# binary_tree_avl.py文件
# 平衡二叉排序树
from trees.binary_sort_tree import BinarySortTree, BinNode2, Assoc
class AVLNode(BinNode2):
def __init__(self, data):
BinNode2.__init__(self, data)
# 初始时平衡因子默认为0
self.bf = 0
class BinaryTreeAvlDict(BinarySortTree):
def __init__(self):
BinarySortTree.__init__(self)
def insert(self, key, value):
"""
插入步骤：
1、如果树中为空，直接插入树中
2、如果树中不为空，插入元素后，更新元素后，看是否有平衡因子绝对值不在[0,1]之间的，如果树已不平衡，进行调整
:param key:
:param value:
:return:
"""
print("开始插入结点！")
root = self._root
if root is None:
self._root = AVLNode(Assoc(key, value))
return
# 树中结点不为空
# 关键的三个结点变量，代表的是被插入元素后受影响的那颗子树的三个结点，进行平衡调整，也是需要调整这三个结点的位置关系
# 1、parent_node代表的是受影响子树的根结点
# 2、subtree_node代表的是还未插入时的受影响子树的叶子结点，可以看做是parent_node的孩子结点
# 3、insert_node代表的是被插入的结点
parent_parent_node = None # 受影响的子树的父结点
parent_node = self._root # 受影响的子树
subtree_node = None
insert_node = None # 被插入点的父结点
parent_root = None
# 首先找到要插入的位置，并将结点插入当前位置
if key == 56:
print("56进来了！")
while root is not None:
data = root.data
if root.bf != 0:
# 得到受影响的子树（最小非平衡子树）与它的父结点
parent_parent_node, parent_node = parent_root, root
parent_root = root
if key < data.key:
# 往左找
if root.left is None:
root.left = AVLNode(Assoc(key, value))
insert_node = root.left
break
root = root.left
elif key > data.key:
# 往右找
if root.right is None:
root.right = AVLNode(Assoc(key, value))
insert_node = root.right
break
root = root.right
else:
# 如果存在key相等，将值覆盖后即可退出
root.data.value = value
return
# 得到新插入结点是插入到parent_node的左子树还是右子树
update_root = None # 更新parent_node下到插入结点所经过结点的所有平衡因子bf
left_or_right = 1 # 1代表左边，-1代表右边，代表着新插入的元素插入到parent_node的哪一边了
while parent_node is not None:
data = parent_node.data
if key > data.key:
left_or_right = -1
update_root = parent_node.right
subtree_node = parent_node.right
else:
update_root = parent_node.left
subtree_node = parent_node.left
break
# 更新从parent_node的左子树结点到插入点路径上的所有bf
while update_root != insert_node:
if key < update_root.data.key:
update_root.bf = 1 # 设置为1，往左边加结点后进行调整，左边树高1，则bf为1
update_root = update_root.left
else:
update_root.bf = -1 # 设置为-1，往右边加结点后进行调整，右边树高1，则bf为-1
update_root = update_root.right
# 如果parent_node的平衡因子为0，更新parent_node的平衡因子即可
if parent_node.bf == 0:
parent_node.bf = left_or_right
return
if parent_node.bf == -left_or_right:
# 新结点插入到了parent_node结点的另一边，那么parent_node趋向平衡
parent_node.bf = 0
return
# 以下是失衡情况
adjust_tree = None
if left_or_right == 1 and subtree_node.bf == 1:
# 当插入的结点在parent_node的左子树，且subtree_node等于1，代表新结点插入在parent_node的左子树的左子树
# LL调整，LL：a的左子树较高，新结点插入在a的左子树的左子树
print(f"结点{key}进行了LL调整")
adjust_tree = self.LL(parent_node, subtree_node)
elif left_or_right == -1 and subtree_node.bf == 1:
# 数据插到了parent_node的右子树上，且subtree_node的平衡因子为1，代表新结点插入在parent_node的右子树的左子树
# RL调整，RL：a的右子树较高，新结点插入在a的右子树的左子树
print(f"结点{key}进行了RL调整")
adjust_tree = self.RL(parent_node, subtree_node)
elif left_or_right == 1 and subtree_node.bf == -1:
# 数据插到了parent_node的左子树上，且subtree_node的平衡因子为-1，代表新结点插入在parent_node的左子树的右子树
# LR调整，LR：a的左子树较高，新结点插入在a的左子树的右子树
print(f"结点{key}进行了LR调整")
adjust_tree = self.LR(parent_node, subtree_node)
elif left_or_right == -1 and subtree_node.bf == -1:
# 数据插到了parent_node的右子树上，且subtree_node的平衡因子为-1，代表新结点插入在parent_node的右子树的右子树
# RR调整，RR：a的右子树较高，新结点插入在a的右子树的右子树
print(f"结点{key}进行了RR调整")
adjust_tree = self.RR(parent_node, subtree_node)
# 将调整后的子树给嫁接上
if parent_parent_node is None:
# 代表parent_node为平衡树的根结点
self._root = adjust_tree
else:
if parent_parent_node.left == parent_node:
parent_parent_node.left = adjust_tree
else:
parent_parent_node.right = adjust_tree
def LL(self, parent_node, subtree_node):
# a的左子树较高，新结点插入在a的左子树的左子树
# 进行旋转
parent_node.left = subtree_node.right
subtree_node.right = parent_node
subtree_node.bf = parent_node.bf = 0
return subtree_node
def RR(self, parent_node, subtree_node):
parent_node.right = subtree_node.left
subtree_node.left = parent_node
parent_node.bf = subtree_node.bf = 0
return subtree_node
def LR(self, parent_node, subtree_node):
c = subtree_node.right
parent_node.left, subtree_node.right = c.right, c.left
c.left, c.right = subtree_node, parent_node
if c.bf == 0:
# c本身就是插入结点
parent_node.bf = subtree_node.bf = 0
elif c.bf == 1:
# 新结点在c的左子树
parent_node.bf = -1
subtree_node.bf = 0
else:
# 新结点在c的右子树
parent_node.bf = 0
subtree_node.bf = 1
c.bf = 0
return c
def RL(self, parent_node, subtree_node):
c = subtree_node.left
parent_node.right, subtree_node.left = c.left, c.right
c.left, c.right = parent_node, subtree_node
if c.bf == 0:
# c本身就是插入结点
parent_node.bf = subtree_node.bf = 0
elif c.bf == 1:
# 新结点在c的左子树
parent_node.bf = 0
subtree_node.bf = -1
else:
# 新结点在c的右子树
parent_node.bf = 1
subtree_node.bf = 0
c.bf = 0
return c
下图为代码的执行结果图
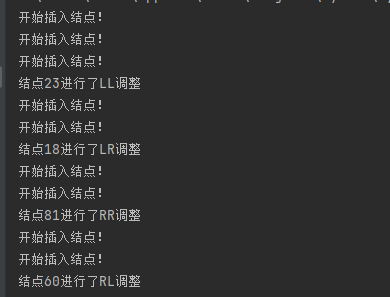
平衡二叉树代码思路解析：
（1）获取要插入结点的位置，将结点插入。（2）更新结点的平衡因子（从平衡树的根结点出发找到平衡因子不等于0的结点，从此结点往下逐步更新）。（3）如果失衡，调整平衡
一棵树：最小的受影响的二叉树，或称为最小非平衡二叉树，通过从被插入结点所遍历过的树路径中，找到平衡因子不为0的结点，此结点则为最小非平衡树的树根，如果不存在平衡因子不为0的结点，则此结点默认为根结点。
三个变量：
在上图（AVL的一系列插入和调整）中，可以看出在出现失衡情况下，只需要调整失衡时的子树的三个结点（根结点、左子树、右子树）的位置关系，并将调整后的子树嫁接到原来的树结点上，则可以恢复失衡。以下是需要维护的三个变量，一个是失衡子树的父结点，用于调整结束后的嫁接工作，第二是失衡子树的根结点，第三是失衡子树的子树。
1、parent_parent_node = None # 受影响的子树的父结点，用于调整后的拼接
2、parent_node = self._root # 受影响的子树的根结点（或称为最小非平衡子树），默认为平衡树的根结点
3、subtree_node = None # 被插入前的子树，为parent_node的子树，
注意上面第三个变量中描述的是个子树而不是结点，这也是为什么需要这个变量的原因，因为如果已经有链接关系了，只需要一个根结点就可以获取到它的子孙。可以参看上图（AVL的一系列插入和调整）中的(10)图，如果再插入一个56的结点，将调整的是（69、60子树、56）三者关系。
两种平衡：
1、在被插入结点时，所受影响的子树平衡因子为0，那么此种情况下为平衡。
2、在被插入结点时，所受影响的子树平衡因子不为0，但新结点插入到了子树空孩子的一边，那么此种情况下为平衡。
四种失衡：
1、左边高，往左边插入结点，插入的是左子结点，失衡
2、左边高，往左边插入结点，插入的是右子结点，失衡
3、右边高，往右边插入结点，插入的是左子结点，失衡
4、右边高，往右边插入结点，插入的是右子结点，失衡
说明：需要拿到三种信息，才能知道是哪种失衡状态，第一种信息，最小非平衡子树的哪边高？可以通过最小非平衡子树（也就是上面变量中的parent_node）的根结点的平衡因子来判断；第二种信息，往最小非平衡子树中插入的结点在哪一边？可以通过遍历最小非平衡子树，通过比较key值，就能拿到新插入结点插入到左边还是右边；第三种信息，插入的是左子结点还是右子结点？可以通过subtree_node的bf来判断，如果等于1则是左子结点，等于-1是右子结点。以上三个步骤都在上述代码中有体现，也是实现平衡二叉树插入操作的核心。可以判断是哪种失衡状态后就可以调用对应的调整函数。
删除操作：删除操作的步骤与插入操作类似，算法可以分为以下几步进行：
1、检索需要删除的结点
2、找到被删结点左子树的最右结点并交换两个结点的位置（这一步理解可以考虑下二叉排序树的性质，左边比根小，右边比根大）
3、实际删除结点
4、如果出现失衡就调整树的结构，恢复平衡
几种二叉排序树的总结
普通二叉排序树：检索的平均效率高，插入和删除的操作实现比较简单，平均操作效率是O(logn)，但是普通二叉排序树在动态修改时，树结构会“恶化”，树的操作效率将会逐步下降。
最优二叉排序树：适合静态字典，构建代价高，构建完成后的检索效率高，但是动态修改后去构建最优树的代价太高，于是不适合动态字典。
平衡二叉排序树：检索效率高，且动态操作（插入与删除）后可以将树维持在一个平衡状态，在长期运行和反复动态修改中，可以始终保证O(logn)的操作复杂性，缺点就是操作的实现比较复杂。
通过平衡二叉树或其它同样性质的结构实现的字典在效率上有确定性的保证，与之对应的散列表实现的字典只有概率性的保证，但是要采用二叉排序树一类结构，还要求数据（或关键码）上有一种合乎需要的序关系。
动态多分支排序树
二叉排序树是以二叉树为基础，一个结点至多有两个分支，主要是控制不同子树的高度差，保证全树高度与所存数据项树之间的对数关系，从而保证了检索效率。而多分支树也可以达到树中结点的个数与树中最长路径的长度呈对数关系，这是实现字典技术的基础。
多分支排序树是另一种实现字典的技术，由于需要保证检索需要沿着树中路径进行，于是还是需要树中结点有序。
多分支排序树的定义：
1、给定一个常量m，多分支排序树中的结点度数不能大于m
2、需要控制树中的路径长度，通过限制多分支排序树中的结点最小度数不能小于某个常量（一般是2或者是m/2）
3、树中的所有叶结点位于同一层，从根到它们的路径等长
4、通过调整兄弟结点之间的关键码以及结点分裂、合并等来维持树的良好结构
B树
一种动态的多分支排序树，B树常用来实现大型数据库（字典）的索引，B树的结点用外存存储块大小的块表示，其中记录的是关键码到数据存储位置的索引，一个结点（存储块）里可能保存很多索引。
B树的性质：
1、定义m为树中最大分支数，也称为树的阶，树中分支结点至多有m-1个排序存放的关键码，根结点至少有一个关键码，其它结点至少有kk((m-1)/2)，kk为取得不大于(m-1)/2的最大整数，所有的叶子结点位于同一层，仅仅用于表示检索失败，实际上并不需要显示。
2、如果一个分支结点有j个关键码，它就有j+1颗子树，这一结点里保存的是一个序列（P0,K0,P1,K1,...,Pj-1,Kj-1,Pj），其中Ki为关键码，Pi为子结点引用，而且Ki大于Pi所引子树里的所有关键码，小于Pi+1所引子树里的所有关键码。
B树图示：
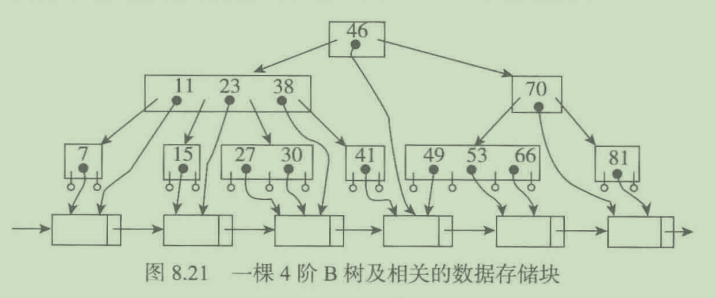
上图为一个4阶B树，图中每个结点有多个关键码，B树中的每个结点都存储着一个数据存储地址的索引值。
B+树
与B树类似的结构，但其概念和实现稍微简单一点，在实际中用的比B树更多。
B+树的性质：
一颗m阶的B+树或者为空，或者满足以下条件：
1、树中每个分支结点至多有m颗子树，除根结点外的分支结点至少有kk(m/2)颗子树，kk的定义参考B树，如果根结点不是叶子结点，至少有两棵子树
2、关键码在结点里顺序存放。分支结点里的每一个关键码关联着一棵子树，这个关键码等于其所关联子树的根结点里的最大关键码，叶结点里的每个关键码关联着一个数据项的存储位置（索引），数据项另行存储
B+树图示：
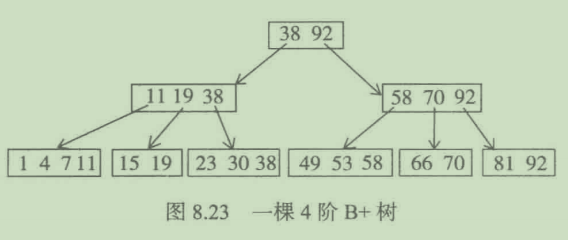
B+树与B树的对比
1、B树每一个结点都关联着数据项，B+树只有叶子结点关联着数据项，B+树比B树简单。
2、B+树的分支结点的关键码不是子树的区分关键码，而是子树的索引关键码，分支结点可以看做索引的索引，整个B+树形成一个分层索引结构。
3、B+树与B树的操作类似
总结
以上的多种树形结构是逐步扩展的实现字典结构，在二叉排序树中来实现字典结构，树结构在动态操作下将会“恶化”，于是需要一个能支持动态操作的字典，在提到支持动态操作的字典（平衡二叉树）之前，又提到了实现静态字典较好的树形结构——最优二叉排序树。平衡二叉树是一个能避免“恶化”的动态字典实现的关键结构，适合用来实现内存字典，但是在实现很大结点的树形结构中，平衡二叉树就没有优势了。于是多分支排序树就来了，它支持存储很大结点的树形结构，在一个结点中存储成千上万的关键码，整个树的结构都不过几层，B树与B+树都是多分支排序树，它们在实现数据库系统的索引上应用广泛。
