清北学堂五一数学营笔记
矩阵
https://www.luogu.com.cn/blog/531930/shou-xie-yi-ge-ju-zhen-lei。
P4159 [SCOI2009] 迷路
如果边权是
这个题有边权且很小(
我们把一个点拆成
我们把
建边我们“向内”建,由
然后是原图的建边。如果
最后我们就得到了一个大小为
由于点的范围是
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
const int mod=2009;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline int read(){
int x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n,tot,t;
inline int id(int x,int y){
return (x-1)*9+y;
}
struct Matrix{
int val[105][105];
Matrix(){
memset(val,0,sizeof(val));
}
inline void reset(){
for(int i=0;i<tot;++i) val[i][i]=1;
}
}tmp;
inline Matrix operator*(const Matrix &a,const Matrix &b){
Matrix c;
for(int i=0;i<tot;++i){
for(int k=0;k<tot;++k){
for(int j=0;j<tot;++j){
c.val[i][j]=(c.val[i][j]+a.val[i][k]*b.val[k][j]%mod)%mod;
}
}
}
return c;
}
inline Matrix ksm(Matrix a,int b){
Matrix c;
c.reset();
while(b){
if(b&1)c=c*a;
a=a*a,b>>=1;
}
return c;
}
signed main(){
n=read(),t=read(),tot=9*n;
for(int i=1;i<=n;++i){
for(int j=1;j<=8;++j) tmp.val[id(i,j)][id(i,j-1)]=1;
for(int j=1;j<=n;++j){
int x;
scanf("%1d",&x);
if(x) tmp.val[id(i,0)][id(j,x-1)]=1;
}
}
tmp=ksm(tmp,t);
println(tmp.val[id(1,0)][id(n,0)]);
return 0;
}
一个小语法
如果你在主函数中定义了一个全局变量
int k=1;
signed main(){
for(int k=2;k<=3;++k) println(k);
return 0;
}
这时候就会输出内部循环中的 ::k 就可以访问到外部的
数论
判断质数
一、试除法
先判断
显而易见的优化是,质因子总是成对出现的,因此只需要枚举较小的那个质因子(不超过
同样的,我们只需要试除质数。可以先
代码太简单,不写了。
二、Miller - Rabin
https://www.luogu.com.cn/paste/0ffg5egd
分解质因数
一、朴素做法
直接枚举
二、Pollard's rho 算法
还没过。
UPD:没讲
CF45G - Prime Problem
纯纯的找规律 & 打表题。
首先我们需要知道哥德巴赫猜想,并且知道它在本题的数据范围内已经得到了验证(也可以自己手动验证)。
首先计算出数列的和
-
如果
-
如果
-
如果
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
const int N=6005;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline int read(){
int x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n,sum,ans[N];
bool vis[N];
inline bool is_prime(int x){
if(x<2)return 0;
for(int i=2;i*i<=x;++i) if(x%i==0)return 0;
return 1;
}
inline void output(){
for(int i=1;i<=n;++i) printsp(ans[i]);
printf("\n");
}
signed main(){
n=read(),sum=n*(n+1)/2;
for(int i=1;i<=n;++i) ans[i]=1;
if(is_prime(sum)){
output();
return 0;
}
if(sum%2==1&&!is_prime(sum-2))sum-=3,ans[3]=3,vis[3]=1;
for(int i=2;i<=n;++i){
if(vis[i])continue;
if(is_prime(i)&&is_prime(sum-i)){
ans[i]=2;
break;
}
}
for(int i=1;i<=n;++i) printsp(ans[i]);
return 0;
}
逆元
若
那么怎么求逆元呢?
费马小定理:
我们发现
然后这个
快速幂计算即可,时间复杂度
所以,在
欧拉函数:
欧拉定理:
这个时候我们会发现如果一个数
这样
注意:逆元存在的充分条件是
最后的问题就是如何算出
一、暴力
枚举
二、优化
暴力的复杂度太高了,我们考虑优化。
-
当
-
当
-
当
-
加一个质因子:当
-
然后就可以得出规律了:将
所以直接分解就可以了,一个小技巧:先除后乘防止溢出。在求
inline int get_phi(int n){
int phi=n;
for(int i=2;i*i<=n;++i){
if(n%i==0){
phi=phi/i*(i-1);
while(n%i==0) n/=i;
}
}
if(n!=1) phi=phi/n*(n-1);
return phi;
}
这样时间复杂度就是
求
移项,得:
除
最后再把
最后,把
写成递推式就是
最后,由于
这种做法还可以拓展到任意
exgcd
给定
假设我们现在要求
现在我们要从这个式子推出
拆项,得:
把带
这个时候,我们发现这个式子和原来的式子形式一样了!因此:
因此只要递归算出
那递归的终止条件呢?当
代码实现时可以用一个三个元素的结构体维护
代码。
用途?
现在有一个问题:
答案是
设
提
所以得数一定是
现在要求
- 把得到的
现在只求出了一组解,求通解怎么办?
- 假设
而且有结论:上述算法取得的一组解
P1082 [NOIP2012 提高组] 同余方程
这个题既然保证有解,那么
做法一:容易发现这个
做法二:我们改写一下它的形式。既然
但是这个题要求最小正整数解。考虑通解公式,容易发现 (%mod+mod)%mod 防止负数即可。
CRT/EXCRT
用途是解如下同余方程组
如果不要求
对于普通 CRT,有一个小构造:记
证明:对于第
对于
筛法
一、暴力
暴力判断每个数是否是质数即可。试除法可以做到
二、埃氏筛
把每个数的倍数筛掉。
not_prime[1]=1;
for(int i=2;i<=n;++i){
for(int j=i+i;j<=n;j+=i){
not_prime[j]=1;
}
}
for(int i=2;i<=n;++i) if(!not_prime[i]) prime[++cnt]=i;
复杂度是多少?
优化:只需要筛质数的倍数。
not_prime[1]=1;
for(int i=2;i<=n;++i){
if(!not_prime[i]){
for(int j=i+i;j<=n;j+=i){
not_prime[j]=1;
}
}
}
for(int i=2;i<=n;++i) if(!not_prime[i]) prime[++cnt]=i;
不加证明地给出算法的复杂度:约为
其实还可以优化:设
not_prime[1]=1;
for(int i=2;i<=n;++i){
if(!not_prime[i]){
for(int j=i*i;j<=n;j+=i){
not_prime[j]=1;
}
}
}
for(int i=2;i<=n;++i) if(!not_prime[i]) prime[++cnt]=i;
三、线性筛
埃氏筛的缺点在于,每个数可能被它的质因子筛了多次。所以它的时间复杂度必然不可能达到
线性筛的思想就是,让每个数被它的最小质因子筛掉。
过程:维护 bool 数组,判断某个数是否是质数;再维护一张质数表,里面存放 break)。
const int N=1e6+5;
int n,prime[N],cnt,T;
bool not_prime[N];
inline void do_prime(){
not_prime[0]=not_prime[1]=1,cnt=0;
for(int i=2;i<=N-5;++i){
if(!not_prime[i])prime[++cnt]=i;
for(int j=1;j<=cnt&&i*prime[j]<=N-5;++j){
not_prime[i*prime[j]]=1;
}
}
}
可惜,这样还是
但是我们只需要在第
if(i%prime[j]==0)break;
这样就
为什么?
当 break 掉了)。而如果 break 掉。 这样就可以保证每个数都是由它的最小质因子筛掉,时间复杂度
代码:
const int N=1e6+5;
int n,prime[N],cnt,T;
bool not_prime[N];
inline void do_prime(){
not_prime[0]=not_prime[1]=1,cnt=0;
for(int i=2;i<=N-5;++i){
if(!not_prime[i])prime[++cnt]=i;
for(int j=1;j<=cnt&&i*prime[j]<=N-5;++j){
not_prime[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}
}
这玩意还能用来筛积性函数。
积性函数
定义:对于一个函数
举个例子:
回忆一下公式:设
那么
假设
所以
而
所以
现在我们要线性求出
首先,
由于我们会筛掉
并不行,因为两者不一定互质。什么时候不互质?
考虑证明,令
由于
容易发现后面的部分就是
这样我们就可以筛出
const int N=1e6+5;
int n,prime[N],cnt,T,phi[N];
bool not_prime[N];
inline void do_prime(){
not_prime[0]=not_prime[1]=phi[1]=1,cnt=0;
for(int i=2;i<=N-5;++i){
if(!not_prime[i])prime[++cnt]=i,phi[i]=i-1;
for(int j=1;j<=cnt&&i*prime[j]<=N-5;++j){
not_prime[i*prime[j]]=1;
phi[i*prime[j]]=phi[i]*phi[prime[j]];
if(i%prime[j]==0){
phi[i*prime[j]]=prime[j]*phi[i];
break;
}
}
}
}
BSGS 算法
Baidu Search Google Search 算法
原题链接。
一、暴力
直接枚举
时间复杂度为
代码还是放一下吧:
inline int solve(int a,int b,int p){
// 求解 a^x % p = b
int val=1;
for(int x=0;x;++x){
if(val==b)return x;
val=1ll*val*a%p;
if(val==1)return -1;// 出现循环,无解
}
}
为什么循环一定从
所以我们改一下:
inline int solve(int a,int b,int p){
// 求解 a^x % p = b
int val=1;
for(int x=0;x<p-1;++x){
if(val==b)return x;
val=1ll*val*a%p;
}
return -1;
}
这样我们就可以喜提
二、正解
由于循环节长度只有
我们将这些数分组,假设每组有
暴力扫描每一个组,复杂度还是一样的。
现在第一组还是暴力,但是我们需要考虑用更快的方法求出后面的组。
很明显,第二组的每个数都是第一组对应数的
我们可以发现,如果第二组存在
换句话说,如果第
这样我们只需要在第一组里面查找了。怎么查找?哈希或者二分。
容易发现这是一个类似分块的操作。我们需要扫描第一组,用哈希维护,时间复杂度
我代码里偷懒用了 set,还写了快速幂,时间复杂度是
代码:
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline ll read(){
ll x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
ll a,b,p;
inline ll ksm(ll a,ll b,ll p){
ll res=1;
a%=p;
while(b){
if(b&1)res=res*a%p;
a=a*a%p,b>>=1;
}
return res;
}
inline ll solve(ll a,ll b,ll p){
// 求解 a^x % p = b
ll s=sqrt(p),val=1;
set<ll>S;
for(int i=0;i<s;++i){
S.insert(val);
val=val*a%p;
}
for(int i=0;1ll*i*s<=p;++i){
// 查找第 i 组(从 0 开始,这样就查找 b/a^si 即可)
ll inv=ksm(a,i*s,p);
ll tmp=b*ksm(inv,p-2,p)%p;
if(S.count(tmp)){
// inv 就是第 i 行的第一个数
for(int j=i*s;;++j){
// 暴力查找第 i 组中满足条件的数
if(inv==b)return j;
inv=inv*a%p;
}
}
}
return -1;
}
signed main(){
p=read(),a=read(),b=read();
int ans=solve(a,b,p);
if(ans==-1)printf("no solution\n");
else println(ans);
return 0;
}
容易发现,每次的循环的
当
提供一个哈希表板子。
由于 Hash 表的时间复杂度是期望线性的,所以时间复杂度
代码:
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
const int N=1e5+5;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline ll read(){
ll x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
ll a,b,p;
inline ll ksm(ll a,ll b,ll p){
ll res=1;
a%=p;
while(b){
if(b&1)res=res*a%p;
a=a*a%p,b>>=1;
}
return res;
}
template<class P,class Q>
struct Hash_Table{
static const int mod=5e5+9;
struct Node{
P key;Q val;
int nxt;
}node[N];
int head[mod+5],cnt;
inline int get_hash(P x){return (x%mod+mod)%mod;}
inline void clear(){
for(int i=1;i<=cnt;++i){
head[get_hash(node[i].key)]=0,node[i].key=node[i].nxt=0;
Q tmp;
swap(node[i].val,tmp);
}
cnt=0;
}
inline void insert(P key){
int val=get_hash(key);
node[++cnt].key=key;
node[cnt].nxt=head[val];
head[val]=cnt;
}
inline Q &operator[](const P key){
int u=get_hash(key);
for(int i=head[u];i;i=node[i].nxt){
P v=node[i].key;
if(v==key)return node[i].val;
}
insert(key);
return node[cnt].val;
}
inline bool count(const P key){
int u=get_hash(key);
for(int i=head[u];i;i=node[i].nxt){
P v=node[i].key;
if(v==key)return 1;
}
return 0;
}
};
Hash_Table<ll,int>mp;
inline ll BSGS(ll a,ll b,ll p){
// 求解 a^x % p = b
ll s=sqrt(p),val=1;
for(int i=0;i<s;++i) mp[val]=i,val=val*a%p;
if(mp.count(b))return mp[b];
ll inv=ksm(ksm(a,s,p),p-2,p),tmp=b%p;
for(int i=1;1ll*i*s<=p;++i){
// 查找第 i 组(从 0 开始,这样就查找 b/a^si 即可)
tmp=(tmp*inv)%p;
if(mp.count(tmp))return mp[tmp]+i*s;
}
return -1;
}
signed main(){
p=read(),a=read(),b=read();
int ans=BSGS(a,b,p);
if(ans==-1)printf("no solution\n");
else println(ans);
return 0;
}
也可以换成 unorderep_map 或者 gp/cc_hash_table,但是性能会差一点。
组合数学
基础知识
加法原理:两种选择是有关系/矛盾的,不能同时选择(同一阶段)。
乘法原理:两种选择是没有关系的,可以同时选择(不同阶段)。
排列:从
对于第一个人,有
由于每个人的选择是独立的,所以乘法原理:
ZHX 语录:小学奥数里用
组合:从
组合
定义式:
现在来考虑一些性质:
-
-
-
递推式:
-
-
当
相当于证明选偶数个物品的方案数等于选奇数个物品的方案数的方案数。
考虑递推式:
-
二项式定理:
-
把
例题
一、
首先考虑每个数只能选一次的情况。将选的数排序,实际上就是求不等式
那么我们怎么把
二、求
- 部分分一:
弱智档,输出
- 部分分二:
递推求组合数即可。
- 部分分三:
递推求出阶乘和阶乘逆元,然后套公式即可。
- 部分分四:
先约分,得:
容易发现,把乘法拆开,分子和分母的项数都是
由于最后的答案一定是整数,所以我们 gcd,所以时间复杂度
还是写一下代码:
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline int read(){
int x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n,m,fz[1005],fm[1005],mod;
ll ans;
int gcd(int x,int y){
return y?gcd(y,x%y):x;
}
signed main(){
n=read(),m=read(),mod=read();
for(int i=1;i<=m;++i) fz[i]=n-i+1,fm[i]=i;
for(int i=1;i<=m;++i){
for(int j=1;j<=m;++j){
int g=gcd(fz[i],fm[j]);
fz[i]/=g,fm[i]/=g;
}
}
ans=1;
for(int i=1;i<=m;++i) ans=(ans*fz[i])%mod;
println(ans);
return 0;
}
- 部分分五:
这里引入一种新的定理:Lucas 定理。
内容:
其中因为
终止条件:
实际上,观察上述式子,发现答案实际上就是将
那么
这样我们就得到了一个迭代做法:先暴力预处理出组合数,用短除法将
时间复杂度
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,p,C[105][105];
int num_a[105],tot_a,num_b[105],tot_b;
inline int Lucas(int a,int b,int p){
memset(num_a,0,sizeof(num_a));
memset(num_b,0,sizeof(num_b));
tot_a=tot_b=0;
while(a) num_a[++tot_a]=a%p,a/=p;
while(b) num_b[++tot_b]=b%p,b/=p;
int ans=1;
for(int i=1;i<=tot_a;++i) ans=1ll*ans*C(num_a[i],num_b[i])%p;
return ans;
}
signed main(){
scanf("%d%d%d",&n,&m,&p);
C[0][0]=1;
for(int i=1;i<p;++i){
C[i][0]=1;
for(int j=1;j<p;++j) C[i][j]=(C[i-1][j]+C[i-1][j-1])%p;
}
printf("%d\n",Lucas(n,m,p));
return 0;
}
实际上直接处理阶乘和阶乘逆元就可以达到
#include<bits/stdc++.h>
const int N=1e5+5;
using namespace std;
int T,n,m,p,fac[N],invfac[N];
int num_a[105],tot_a,num_b[105],tot_b;
inline int ksm(int a,int b){
int res=1;a%=p;
while(b){
if(b&1)res=1ll*res*a%p;
a=1ll*a*a%p,b>>=1;
}
return res;
}
inline int C(int n,int m){
if(n<m||n<0||m<0)return 0;
return 1ll*fac[n]*invfac[m]%p*invfac[n-m]%p;
}
inline int Lucas(int a,int b,int p){
memset(num_a,0,sizeof(num_a));
memset(num_b,0,sizeof(num_b));
tot_a=tot_b=0;
while(a) num_a[++tot_a]=a%p,a/=p;
while(b) num_b[++tot_b]=b%p,b/=p;
int ans=1;
for(int i=1;i<=tot_a;++i) ans=1ll*ans*C(num_a[i],num_b[i])%p;
return ans;
}
signed main(){
scanf("%d",&T);
while(T--){
scanf("%d%d%d",&n,&m,&p);
fac[0]=1,n+=m;
for(int i=1;i<p;++i) fac[i]=1ll*fac[i-1]*i%p;
invfac[p-1]=ksm(fac[p-1],p-2);
for(int i=p-2;i>=0;--i) invfac[i]=1ll*invfac[i+1]*(i+1)%p;
printf("%d\n",Lucas(n,m,p));
}
return 0;
}
假设要求
质因数分解,
然后直接上 CRT 就行。
实际上,当
但是如果
习题
一、给定
-
-
原题是 Luogu P4369。
代码:
#include<bits/stdc++.h>
using namespace std;
int x,k;
signed main(){
scanf("%d%d",&x,&k);
for(int i=1;i<k;++i) printf("%d %d\n",i,0);
printf("%d %d\n",x-k+1,1);
return 0;
}
二、比较
对数函数的性质:
同理,有
如果
这样,我们只需要求
我们算一下:
现在怎么算阶乘的
所以
然后我们就可以递推算出阶乘的
这样我们就可以比较大小了。
至于底数
实际上类似于放缩法,缩小答案的范围然后计算。
代码(把缺省源砍了):
#include<bits/stdc++.h>
//typedef __uint128_t ulll;
const int N=1e6+5;
using namespace std;
int n1,m1,n2,m2;
double fac[N];
inline double logC(int n,int m){
return fac[n]-fac[m]-fac[n-m];
}
signed main(){
cin>>n1>>m1>>n2>>m2;
fac[0]=0;
for(int i=1;i<=N-5;++i) fac[i]=fac[i-1]+log(i);
double _1=logC(n1,m1),_2=logC(n2,m2);
if(_1>_2) printf("A > B\n");
else if(_1==_2) printf("A = B\n");
else printf("A < B\n");
return 0;
}
时间复杂度
还有个问题:这里用的 double,精度怎么办?
精度误差影响的是小数点后好几位,和这个题没关系。
三、选
首先,最大的组合数是什么?
考虑杨辉三角的性质,明显是最后一行最中间的那个数(有偶数列的话就除二即可)。
那第二大的呢?
明显是在最大的上下左右。现在不知道谁更大,比较一下即可(上一题刚说过)。
然后从第二大的数又可以往四周扩充几个点。维护一个候选集,每次从候选集里面挑选一个最大的,取出来之后更新候选集,重复
很明显,这是一个类似 BFS 的过程。
注意判重。
Luogu 原题是 P4370。
代码(我每次加入的是当前点周围八联通的点):
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
const int N=1e6+5;
const int dx[8]={-1,-1,0,1,1,1,0,-1};
const int dy[8]={0,1,1,1,0,-1,-1,-1};
const int mod=1e9+7;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline int read(){
int x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n,k,facc[N],ifac[N];
double fac[N];
map<int,map<int,bool> >mp;
inline ll ksm(ll a,ll b){
ll res=1;
a%=mod;
while(b){
if(b&1)res=res*a%mod;
a=a*a%mod,b>>=1;
}
return res;
}
inline double logC(int n,int m){
return fac[n]-fac[m]-fac[n-m];
}
inline bool outmp(int x,int y){
return x<0||x>n||y<0||y>n;
}
struct Binom{
int x,y;
// C(x,y)
Binom(int _x=0,int _y=0):x(_x),y(_y){}
inline bool operator<(const Binom &b)const{return logC(x,y)<logC(b.x,b.y);}
};
priority_queue<Binom,vector<Binom>,less<Binom> >pq;
inline ll C(int n,int m){
if(n<m||n<0||m<0)return 0;
return 1ll*facc[n]*ifac[m]%mod*ifac[n-m]%mod;
}
signed main(){
n=read(),k=read(),fac[0]=0,facc[0]=1;
for(int i=1;i<=n;++i) fac[i]=fac[i-1]+log(i),facc[i]=1ll*facc[i-1]*i%mod;
ifac[n]=ksm(facc[n],mod-2);
for(int i=n-1;i>=0;--i) ifac[i]=1ll*ifac[i+1]*(i+1)%mod;
pq.push(Binom(n,(n+1)/2));
int cnt=0;
ll ans=0;
while(cnt<k){
int x=pq.top().x,y=pq.top().y;
pq.pop();
if(mp[x][y])continue;
mp[x][y]=1;
ans=(ans+C(x,y))%mod,cnt++;
for(int i=0;i<8;++i){
int xx=x+dx[i],yy=y+dy[i];
if(outmp(xx,yy))continue;
pq.push(Binom(xx,yy));
}
}
println(ans);
return 0;
}
四、P3746 [六省联考 2017] 组合数问题
原题链接。
这个题
我们记
现在我们来介绍几个求和变形的技巧:
一、增加枚举量
把
二、交换枚举顺序
明显交换两个
三、分离无关变量
容易发现此时
然后我们把式子整理一下:
我们会发现,第二个
我们使用一个经典套路:给他扩充一维,凑成矩阵乘法:
这个时候我们把
对比原式,只需要令
这样就能用矩阵乘法了。
有
我们有
很明显,只有当
所以,
但还有一个问题:
我们考虑证明:
把
实际上,因为
这样,如果
然后我们就可以直接进行矩阵乘法了(由于预处理时已经解决了负数的情况,所以直接从
这样我们就做完了。时间复杂度
代码:
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
const int N=55;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline int read(){
int x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n,p,k,r,C[N][N];
struct Matrix{
int n,m;
ll val[N][N];
Matrix(int _n=0,int _m=0){
n=_n,m=_m;
memset(val,0,sizeof(val));
}
}f0,D;
inline Matrix operator*(const Matrix &a,const Matrix &b){
Matrix c(a.n,b.m);
for(int i=0;i<c.n;++i){
for(int k=0;k<a.m;++k){
for(int j=0;j<c.m;++j){
c.val[i][j]=(c.val[i][j]+a.val[i][k]*b.val[k][j]%p)%p;
}
}
}
return c;
}
inline Matrix ksm(Matrix a,int b){
Matrix c=a;
b--;
while(b){
if(b&1)c=c*a;
a=a*a,b>>=1;
}
return c;
}
signed main(){
n=read(),p=read(),k=read(),r=read();
C[0][0]=1;
for(int i=1;i<=k;++i){
C[i][0]=1;
for(int j=1;j<=k;++j) C[i][j]=(C[i-1][j]+C[i-1][j-1])%p;
}
f0.n=1,f0.m=k+1;
f0.val[0][0]=1;
for(int j=1;j<=k;++j) f0.val[0][j]=0;
D.n=D.m=k+1;
for(int r=0;r<=k;++r){
for(int j=0;j<=k;++j){
if(r>=j) D.val[r][r-j]+=C[k][j];
else D.val[r][r-j+k]+=C[k][j];
}
}
Matrix F=f0*ksm(D,n);
println(F.val[0][r]);
return 0;
}
抽屉原理
把
推广:把
习题
一、POJ 3370
给定
奇怪的地方是
构造:强制令选的数连续。做一遍前缀和,那么需要满足 vector,把前缀和的编号插入里面,最后找到 size()>1 的一组,取出里面的两个编号即可。
代码:
#include<cstdio>
#include<vector>
const int N=1e5+5;
using namespace std;
int c,n,a[N],sum[N];
vector<int>box[N];
signed main(){
while(1){
scanf("%d%d",&c,&n);
if(!c&&!n)break;
for(int i=0;i<c;++i) box[i].clear();
sum[0]=0;
for(int i=1;i<=n;++i){
scanf("%d",a+i);
sum[i]=(sum[i-1]+a[i]%c)%c;
}
for(int i=0;i<=n;++i) box[sum[i]%c].push_back(i);
for(int i=0;i<c;++i){
if(box[i].size()>1){
int l=box[i][0],r=box[i][1];
for(int i=l+1;i<=r;++i) printf("%d ",i);
break;
}
}
printf("\n");
}
return 0;
}
二、P2218 [HAOI2007]覆盖问题
原题链接。
平面上有
首先发现答案满足单调性,考虑二分。
现在的问题就是如何 check:找到最左、最右、最上、最下的四个点,然后画一个大长方形;根据抽屉原理,必然有一个正方形要盖住两个。很明显这个正方形要放在大长方形的角上。由于点数很小,可以直接暴力枚举盖哪个角。使用 dfs 递归三层即可,具体来说:
第一层递归:找到四个极限点,枚举盖住哪个角,进入下一层;
第二层递归:找到没被覆盖的四个极限点,枚举盖住哪个角;
第三层递归:找到没被覆盖的四个极限点,判断横纵坐标的最大差值是否
注意使用下一个正方形的时候要清空当前被覆盖的点。
代码:
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
const int N=2e4+5;
const int inf=1e9+1;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline int read(){
int x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n,flag[N];
struct Point{
int x,y;
Point(int _x=0,int _y=0):x(_x),y(_y){}
inline void reset(){x=y=0;}
}a[N];
struct Square{
Point up_left,down_right;
Square(){
up_left.reset();
down_right.reset();
}
};
inline bool in(Point a,Square b){
// 判断 a 是否在 b 内
return a.x>=b.up_left.x&&a.x<=b.down_right.x&&a.y>=b.down_right.y&&a.y<=b.up_left.y;
}
bool dfs(int k,int dep){
// k * k,当前是第 dep 个正方形
Point L(inf,0),R(-inf,0),U(0,-inf),D(0,inf);
for(int i=1;i<=n;++i){
if(a[i].x<L.x&&!flag[i]) L=a[i];
if(a[i].x>R.x&&!flag[i]) R=a[i];
if(a[i].y>U.y&&!flag[i]) U=a[i];
if(a[i].y<D.y&&!flag[i]) D=a[i];
}
if(max(1ll*R.x-L.x,1ll*U.y-D.y)<=k) return 1;
if(dep==3) return 0;
Square r[4];
r[0].up_left=Point(L.x,U.y),r[0].down_right=Point(L.x+k,U.y-k);// 左上角
r[1].up_left=Point(R.x-k,U.y),r[1].down_right=Point(R.x,U.y-k);// 右上角
r[2].up_left=Point(L.x,D.y+k),r[2].down_right=Point(L.x+k,D.y);// 左下角
r[3].up_left=Point(R.x-k,D.y+k),r[3].down_right=Point(R.x,D.y);// 右下角
for(int i=0;i<4;++i){
// 使用第 i 个正方形
for(int j=1;j<=n;++j) if(!flag[j]&&in(a[j],r[i])) flag[j]=dep;// 覆盖
if(dfs(k,dep+1)) return 1;
for(int j=1;j<=n;++j) if(flag[j]==dep) flag[j]=0;
}
return 0;
}
inline bool check(int k){
for(int i=1;i<=n;++i) flag[i]=0;
return dfs(k,1);
}
signed main(){
n=read();
for(int i=1;i<=n;++i) a[i].x=read(),a[i].y=read();
int l=0,r=2*inf;
while(l<r){
int mid=l+((r-l)>>1);
if(check(mid)) r=mid;
else l=mid+1;
}
println(l);
return 0;
}
容斥原理
那么我们有:
同理可得:
推广到
习题
一、N 对夫妻问题
做完了吗?并没有,因为情况会算重。因此,加回来(使两对夫妻强制相邻):
同理,最终可得:
这个
二、P9118 [春季测试 2023] 幂次/ HDU 2204
可以啊,春测出原题。
首先我们发现
记 powl(1.0*n,1.0/i) 就可以求出来(是 long long,一定要开 powl!!!)。
然后发现
不超过一百是因为
我们发现编号较小的
最后再加上
代码:
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
ll n,ans,dp[105];
int k;
signed main(){
scanf("%lld%d",&n,&k);
for(int i=100;i>=k;--i){
dp[i]=powl(1.0*n,1.0/i)-1;
for(int j=2;j*i<=100;++j) dp[i]-=dp[i*j];
}
ans=1;
for(int i=k;i<=64;++i) ans+=dp[i];
printf("%lld\n",ans);
return 0;
}
HDU 2204 就把
矩阵 - 二
高斯消元
原理已经写过了,见本文最开头的链接。
用处:
一个题,输入一个数,输出一个数,通常会怎么做?
打表!
分块打表!
OEIS!
找规律!
这个过程就可以用高消。
比如,一个数列在
我们猜测:答案是形如
解出来,得:
试一下,好像不对。那就加一次,加个未知数。最终可以试出来
这个解方程的过程就可以使用高斯消元。
限制条件:答案必须是形如若干个
这实际上是一种骗分技巧。
矩阵求逆
定义:见模板题。
考虑如下矩阵:
容易发现,它和单位矩阵的唯一区别就是第
如果用它左乘一个矩阵,那么将会交换这个矩阵的第二、第三行。
再考虑如下矩阵:
如果它左乘一个矩阵,那么将会把那个矩阵的第一行
我们会发现,这正好是高斯消元的操作!
这样,高斯消元的过程就可以转化为矩阵乘法了。
我们考虑把
怎么一起消呢?把两个矩阵放一块即可。
代码还是在文章最开头的博客里。
概率与期望
概率
假设我们要扔骰子,那么扔出来的结果
既然事件是集合,那么它们之间也可以进行运算。设
那减法呢?
样本空间内每个样本点都有一个概率,每个样本点的概率不一定相等。一个事件的概率就是事件内样本点的概率之和。
接下来介绍概率的一些性质:
-
-
假设样本空间内共有
-
如果
条件概率:
再举个例子,如果
实际上,条件概率有一个更简单的公式:
解释:如图,
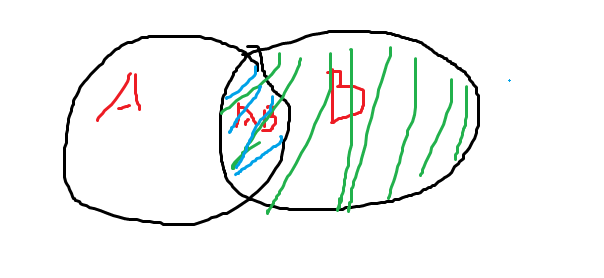
如果
所以,还可以得出
独立事件:如果
实际上,对比条件概率的公式,有:
这也可以解释:由于这两个事件独立,所以
比如,扔两次骰子,这两个事件就是互相独立的。
期望
还是扔骰子,每个数的概率都是
期望,实际上就是每个事件的权值(比如扔骰子的期望)
那如果是扔出来的数的平方的期望呢?同理,为:
接下来,介绍一下期望的性质:
- 期望的和
实际上,这在任何情况下都适用:
这也是对的。这样,就可以大大降低运算量。
严谨证明?不会
习题
一、课件 P111
某小区有男
很明显,这是求
剩下懒得约分了。
二、课件 P117 - 小葱过河
问题在于比较
发现指数可以约掉,问题变为比较
考虑放缩法,由于
约分,得:
所以,答案是不过河走那
三、课件 Question 11 - 小胡抛硬币
操作二和操作三之间的那个点非常关键,我们考虑枚举它的坐标。
显然,最坏情况下会走无限步,所以
-
首先,我们需要走到
-
然后,我们需要走到
-
最后,我们需要原路返回。很明显,我们一共需要抛
把上面三个部分乘起来(不是一个阶段),然后枚举
我们考虑用求和变形技巧化简式子。
首先,把能合并的合并,有:
然后我们介绍第四个求和变形的技巧:
- 换元法:我们令
分离无关变量:
这是什么?二项式定理!
所以:
剩下的是什么?是等比数列。
我们可以使用等比数列求和公式:
所以:
分子分母取相反数,得:
在极限意义下,
问题来了:当
实际上,当
四、BZOJ 2396
可以在 Dark BZOJ 上交。网址。
梯子在这里。
我们可以构造一个
首先,
但是反过来对吗?
明显不对,比如
但是我们多随几次,正确率就很高了。
代码(我随了十次):
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
//typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
//typedef __int128 lll;
//typedef __uint128_t ulll;
const int N=1005;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline ll read(){
ll x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n;
struct Matrix{
int n,m;
ll val[N][N];
Matrix(int _n=0,int _m=0){
n=_n,m=_m;
memset(val,0,sizeof(val));
}
inline void Reader(){
for(int i=0;i<n;++i) for(int j=0;j<m;++j) val[i][j]=read();
}
inline void Output(){
for(int i=0;i<n;++i){
for(int j=0;j<m;++j) printsp(val[i][j]);
printf("\n");
}
}
inline bool operator==(const Matrix &b)const{
for(int i=0;i<n;++i) for(int j=0;j<m;++j) if(val[i][j]!=b.val[i][j]) return 0;
return 1;
}
}A,B,C;
inline Matrix operator*(const Matrix &a,const Matrix &b){
Matrix c(a.n,b.m);
for(int i=0;i<c.n;++i){
for(int k=0;k<a.m;++k){
for(int j=0;j<c.m;++j){
c.val[i][j]+=a.val[i][k]*b.val[k][j];
}
}
}
return c;
}
mt19937 Rand(time(0));
inline bool check(Matrix a,Matrix b,Matrix c){
// 检查 a * b 是否 = c
Matrix Vector(c.m,1);
for(int i=0;i<Vector.n;++i) Vector.val[i][0]=Rand();
return a*(b*Vector)==c*Vector;
}
inline void solve(){
A.n=C.n=A.m=B.n=B.m=C.m=n;
A.Reader(),B.Reader(),C.Reader();
for(int i=1;i<=10;++i){
if(!check(A,B,C)){
printf("No\n");
return;
}
}
printf("Yes\n");
}
signed main(){
while(~scanf("%d",&n)) solve();
return 0;
}
注意 check 函数的最后,要加括号,不然复杂度就伪了。
这题在 luogu 上有个原:P10102。
不过这题只需要随一次就行了,题解说错误率是
贴个码:
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define gt getchar
#define pt putchar
#define fst first
#define scd second
#define SZ(s) ((int)s.size())
#define all(s) s.begin(),s.end()
#define pb push_back
#define eb emplace_back
typedef long long ll;
typedef double db;
typedef long double ld;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N=3005;
const int mod=998244353;
using namespace std;
using namespace __gnu_pbds;
typedef pair<int,int> pii;
template<class T,class I> inline void chkmax(T &a,I b){a=max(a,(T)b);}
template<class T,class I> inline void chkmin(T &a,I b){a=min(a,(T)b);}
inline bool __(char ch){return ch>=48&&ch<=57;}
template<class T> inline void read(T &x){
x=0;bool sgn=0;static char ch=gt();
while(!__(ch)&&ch!=EOF) sgn|=(ch=='-'),ch=gt();
while(__(ch)) x=(x<<1)+(x<<3)+(ch&15),ch=gt();
if(sgn) x=-x;
}
template<class T,class ...I> inline void read(T &x,I &...x1){
read(x);
read(x1...);
}
template<class T> inline void print(T x){
static char stk[70];short top=0;
if(x<0) pt('-');
do{stk[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top) pt(stk[top--]);
}
template<class T> inline void printsp(T x){
print(x);
putchar(' ');
}
template<class T> inline void println(T x){
print(x);
putchar('\n');
}
int T,n,a[N][N],b[N][N],c[N][N],d[N];
int res1[N],res2[N],res3[N];
inline void add(int &a,int b){
a+=b;
if(a>=mod) a-=mod;
}
mt19937 Rand(time(0));
inline void solve(){
read(n);
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) read(a[i][j]);
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) read(b[i][j]);
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) read(c[i][j]);
for(int i=1;i<=n;++i) d[i]=Rand()%mod,res1[i]=res2[i]=res3[i]=0;
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
add(res1[i],1ll*d[j]*a[j][i]%mod);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
add(res2[i],1ll*res1[j]*b[j][i]%mod);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
add(res3[i],1ll*d[j]*c[j][i]%mod);
}
}
for(int i=1;i<=n;++i) if(res2[i]!=res3[i]) return printf("No\n"),void();
printf("Yes\n");
}
signed main(){
read(T);
while(T--) solve();
return 0;
}
显然
但是原来的代码过不了,说明不用封装的时候别 xjb 封装净增常数。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理