CF542E Playing on Graph

图论思维好题，值得一做。

考虑怎样的情况是一定不合法的。结论：图不合法当且仅当存在奇环。

充分性证明：（1）三角形不合法；（2）任意缩奇环中的两个点将产生一个更小的奇环。

必要性证明：没有奇环的图为二分图，而二分图一定可以缩成链（*）

因为连接两条链会产生一条长度为两条链的和的一条新链，故考虑在每个二分联通子图中找出最长链即可。

考虑以一个点\(x\)作为链的起点，建一棵\(bfs\)树。

由于是二分图，\(bfs\)树同一层节点之间没有连边。

由于是\(bfs\)树，每个点的连边只能在相邻一层的范围内，且必定和上一层节点有连边。

那么我们把同一层节点缩在一起，就可以得到一条链（这也证明了*结论）。

思考为何此链为最长链。考虑若结论错误，则必存在如下回环的结构：

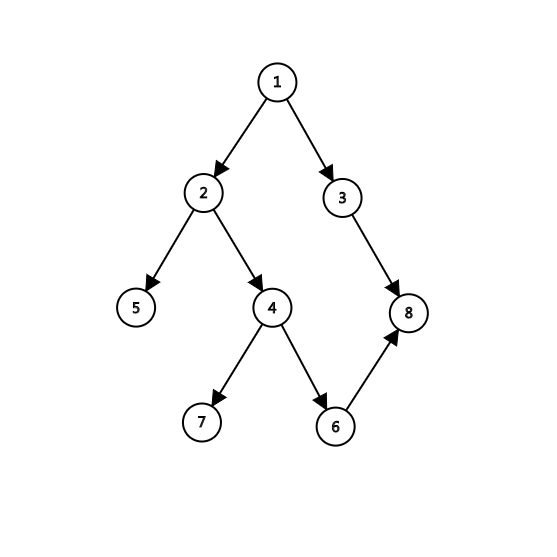
如图中的\(1\rightarrow 2\rightarrow 4\rightarrow 6\rightarrow 8\)

为了保持这条链的结构，则只能想办法通过缩\(1\rightarrow 8\)上的点断开\(1\rightarrow 8\)，然而缩点并不干扰连通性，故不可能。

时间复杂度\(\Theta(n^2)\)，由于\(n\leq 1000\)，可以通过本题。

参考了这篇博客，他写的很好。

代码如下，仅供参考：

#include<bits/stdc++.h>
using namespace std;
#define inf 1e9
const int N=1005;
const int maxn=2e5+10;
int n,m,dis[N],len[N],ans;
inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
	return x*f;
}
int beg[N],nex[maxn],to[maxn],w[maxn],e;
inline void add(int x,int y){
	e++;nex[e]=beg[x];
	beg[x]=e;to[e]=y;
}
int bel[N],col[N],scc,flag;
inline void dfs(int x){
	bel[x]=scc;
	for(int i=beg[x];i;i=nex[i]){
		int t=to[i];
		if(!bel[t])col[t]=1^col[x],dfs(t);
		else if(col[x]==col[t])flag=1;
	}
}
queue<int>q;
inline void bfs(int x){
	memset(dis,-1,sizeof(dis));
	q.push(x);dis[x]=0;
	while(!q.empty()){
		int x=q.front();
		q.pop();
		for(int i=beg[x];i;i=nex[i]){
			int t=to[i];
			if(dis[t]==-1){
				dis[t]=dis[x]+1;
				q.push(t);
			}
		}
	}
}
int main(){
	n=read(),m=read();
	int x,y;
	for(int i=1;i<=m;i++){
		x=read(),y=read();
		add(x,y),add(y,x);
	}
	for(int i=1;i<=n;i++)
		if(!bel[i])scc++,dfs(i);
	if(flag)return puts("-1"),0;
	for(int i=1;i<=n;i++){
		bfs(i);
		for(int j=1;j<=n;j++)
			len[bel[j]]=max(len[bel[j]],dis[j]);
	}
	for(int i=1;i<=scc;i++)
		ans+=len[i];
	printf("%d\n",ans);
	return 0;
}

深深地感到自己的弱小。