动态规划理解-Dynamic Programming

   【原文见： http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=dynProg】   

    Dynamic programming (简称DP)可以用来解决一类很重要的问题。解决这类问题将会极大的提高你的能力。我将试着帮助您了解如何使用DP来解决问题。这篇文章以例子作为基础，因为空谈理论不太容易理解。

    注意:  如果您不太想阅读某节或者已经知道了所要讨论的话题-略过它去读下面的部分。

Introduction (Beginner)

什么是动态规划,它怎样描述?

    动态规划作为一种算法技巧，通常基于一个递推方程和一个(或者多个)初始状态。一个问题的子问题可以从前面已经知道结果的问题中得到。使用DP通常可以得到多项式的时间复杂度，因此比起回溯，暴力等方法，它显得更加快些。
    现在我们借助一个例子来了解下DP的基础知识:
给定N个硬币,它们的面值是(V1,V2,...,VN)，并且提供一个总和为S。现在需要找出一个方案，使得用最少的硬币构成S(我们可以无限次使用某种面值的硬币),或者说明根本不可能有一种方案可以组成S。
      现在让我们开始构造一个DP的解决方案: 首先我们需要找到一个已经使用最优方案的状态，借助它，我们可以得到下一个最优方案的状态。

"状态"是什么意思?

    它是一个用来描述某个问题的子问题,某种情况的一个方式。例如，一个状态可以是某个硬币总和i(i <= S)。比状态i更小的状态可以是任意的硬币总和j(j < i)。为了找到一个状态i,我们需要找到所有的小的状态j(j < i)。找到组成硬币总和i的最少硬币总数之后，我们可以很容易的计算下一个状态--i+1的最优方案。

怎样找出这些状态?

      非常简单-对于每一个硬币j,Vj<=i，查询一下构成i-Vj硬币总和所需要的最少硬币数目(我们之前已经计算过了)。不妨假设这个数字是m,如果m+1小于所求得硬币总和为i的最少硬币数量,我们更新它的状态。为了更好的理解这个问题,我们举例如下: 给定面值为1，3和5的硬币,给定的硬币总和S为11。
 
     首先我们标记状态0(硬币总和0)所需要的最少硬币数目为0.下面我们计算硬币总和1。首先，我们需要标记出这个状态未找到最优解（赋值为无穷大就可以了）。然后我们看到只有面值为1的硬币小于等于当前的总和。通过分析，我们可以看到1-V1=0,并且硬币为0的方案已经计算好了。因为我们在这个方案基础上加上了1，因此我们得到了总和为1的一个方案，所需硬币个数为1。对于这个硬币总和，这是唯一能够找到的方案。我们记下状态。然后我们处理下一个状态-总和为2.我们发现少于这个总和的只有第一个硬币1。对于硬币总和(2-1)=1的最优解是硬币1.硬币1加上第一个硬币将得到硬币总和为2，并且可以用2枚硬币得到硬币总和2。这对于硬币总和2来说是最优的也是仅有的方案。下面我们继续处理硬币总和3。由于我们已经分析了两种硬币总和，并且第一个硬币和第二个硬币的面值为1和3。我们先看第一个，不难发现，可以通过2(3-1)构建出总和为3的一种方案。对于硬币总和为2来说我们找到的最优解法需要2枚硬币，因此硬币总和3的新的方案需要3枚硬。现在让我们来看第二个硬币。我们可以从0的基础上假上3得到硬币总和3.我们知道硬币总和为0的情况需要0枚硬币。因此硬币总和3仅需要一枚硬币即可-3。我们看到这个方案要比前面一个方案所需要的硬币数量上，因此我们更新它，并且标记它仅需要一枚硬币就能得到。对于硬币总和4，我们进行同样的处理，得到的结果是2个-1+3。如此下去。

伪代码:

Set Min[i] equal to Infinity for all of i
Min[0]=0

For i = 1 to S
For j = 0 to N - 1
   If (Vj<=i AND Min[i-Vj]+1<Min[i])
Then Min[i]=Min[i-Vj]+1

Output Min[S]

下面是一些硬币总和的方案数: 

Sum Min. nr. of coins Coin value added to a smaller sum to
obtain this sum (it is displayed in brackets)
0 0 -
1 1 1 (0)
2 2 1 (1)
3 1 3 (0)
4 2 1 (3)
5 1 5 (0)
6 2 3 (3)
7 3 1 (6)
8 2 3 (5)
9 3 1 (8)
10 2 5 (5)
11 3 1 (10)



    结果我们就得到了一个组成硬币总和11需要3枚硬币的方案。此外，如果如果我们记录下从前一个状态得到当前状态所需要的硬币，我们可以找出组成该硬币总和所需要的所有硬币。例如:要组成硬币总和11，我们可以通过面值为1的硬币加上面值为10的硬币。为了得到10，我们需要得到5，而5需要从0，因此我们找到了所使用到的硬币:1,5和5。

   了解了DP的一些基本的套路，现在让我们从一个不同的角度来看待这个问题。无论何时对于一个硬币总和我们发现了一个更优的解，我们都需要去更新它。在这种情况下状态并不是连续计算的。继续考虑上面的那个例子。已知了硬币总和为0需要0枚硬币。现在我们试图在所有已经知道的结果中加上第一个，硬币（面值为1）。如果硬币总和t比起它的前一个状态需要的硬币数量更少，我们将更新它。对于第二个硬币，第三个硬币，和剩下的都是这样处理。例如，我们首先在硬币总和0上加上1得到硬币总和1.因为我们还未找到一个方法组成1-因此这是目前找到的最佳方案，我们标记S[1]=1。通过在硬币总和1上加上1，我们得到了硬币总和2，我们标记S[2]=2。然后对于第一个硬币依次下去。当第一个硬币处理完之后，取出第二个硬币（面值为3），并在所有已经找出的硬币总和上加上3。在0上加3我们得到了硬币总和3需要一枚硬币，到目前为止，S[3]是等于3的，而现在新的方案要比这个先前的方案要更加的好，我们更新它并将它标记为S[3]=1。在硬币总和1上加上相同的硬币，我们得到了可以用2枚硬币得到硬币总和4。之前我们发现的硬币总和4需要4枚硬币组成；现在找到了一个更好的方案，我们更新S[4]为2。对于下面的硬币总和，我们照着上面这样一次下面-一旦一个更优的方案找到，结果将会被更新。


Elementary

   之前我们已经讨论过了非常简单的例子。现在让我们看看在一些复杂问题中如何找出一种从一个状态转移到另外一个状态的方法。在此之前，我们将会介绍一个新的词汇--转移关系，它使得一个较低的一个状态能和较高的状态联系在一起。
    
    让我们看看它是如何工作的：

给定N个数字序列-A[1],A[2],...,A[N]。找出最长不下降子序列。

    正如上面所说，我们需要找出怎样定义代表子问题的一个"状态"，并找出一个解决方案。注意在大多数情况下，状态只依赖与较低的状态而独立与较高的状态。我们定义状态i为最后数字为A[i]的最长不下降子序列。这个状态只保存这个序列的长度。注意对i<j而言，状态i和j是独立的，也就是说在计算j状态的时候，是不会影响状态i的。现在让我们看看这些状态怎样互相联系的。在找出所有小于i的状态解决方案之后，我们会找状态i，首先我们初始化它的结果为1，也就是仅仅包含自身。现在对每个j<i，我们看从它是否能够到达状态i。只有当A[j]<=A[i]以后才可以,才能保证整个序列不下降。 因此如果S[j](为状态j找出的方案)+1(A[i]被增加到以A[j]作为结尾的序列中)要比状态i已经找到的方案要更加好的话(也就是 S[j] + 1>S[i])，我们使得S[i]=S[j]+1。这样我们可以不断的找出每一个状态i的最优方案，知道最后一个状态N。

    现在我们看看对于一个随机生成的序列: 5,3,4,8,6,7 整个过程如何进行: 


I The length of the longest
non-decreasing sequence
of first i numbers		 The last sequence i from
which we "arrived"
to this one
1 1 1 (first number itself)
2 1 2 (second number itself)
3 2 2
4 3 3
5 3 3
6 4 4



练习题:
    给定一个有N(1<N<=1000)个顶点和正权重的无向图。找出从顶点1到顶点N的最短路径，或者说明这样的路径不存在。

    提示:在每一步中，在所有没有被检查的顶点中，如果找出从1到该点的一个最短路径，找出具有最短路径的一条。

试着解决TopCoder比赛中的下面一些问题:

Intermediate

    现在让我们看看如何解决2维DP问题。
问题:
   一个拥有N*M个单元的格子，每一个里面都有着一定数量的苹果，数量已经给定。现在你位于左上角。每一步你可以向下走或者向右走。问你能够收集到最多多少个苹果。

    这个问题可以向其他DP问题一样来解决；几乎没有差别。首先我们需要找出一个状态。首先我们需要注意到到某个单元里最多有两种方法-要么从它的左边过来(如果当前格子不是在第一列的话)，要么从上方过来(如果它不是在最上面的行的话)。为了找到该单元的最优方案，我们首先需要找到到达它的单元的最优方案。从上面的叙述中，我们可以很容易的得到转移关系:
S[i][j]=A[i][j]+max(S[i-1][j],if i>0; S[i][j-1],if j>0) (这里的i代表行，j代表列。左上角的坐标为{0,0}；A[i][j]为i,j单元格中的苹果数量)。

    S[i][j]需要在每行中从左到右计算，并且从上到下计算每一行，或者从上到下计算每一列然后从左到右处理每一列。

伪代码:

For i = 0 to N - 1
   For j = 0 to M - 1
   S[i][j] = A[i][j] +
      max(S[i][j-1], if j>0 ; S[i-1][j], if i>0 ; 0)

Output S[n-1][m-1]

下面是TopCoder比赛中的一些题目，作为练习之用：

Upper-Intermediate

这节将讨论如何处理带有约束条件的DP问题。

下面是一个例子：
       给定一个拥有N个顶点和正权重的无向图G。你在出发前拥有M钱，为了通过顶点i，你需要付S[i]钱。如果你没有足够的钱-你不能通过顶点i。现在要求在上面的条件下找出从顶点1到顶点N的最短路径；或者说明这样的路径不存在。如果存在多条相同长度的路径，输出最便宜的一条。条件: 1<N<=100;0<=M<=100；对每个顶点i，0<=S[i]<=100。正如我们所看到的，这和经典的Dijkstra问题(找出两个顶点间的最短距离)不同的是，这里有一个额外的提交。在经典Dijkstra问题中我们用到了一个一维数组Min[i]，用来标记已经找到的从起点到i的最短距离。尽管如此，在这个问题中，我们应该也要保存我们拥有钱的信息。因此将数组扩展到M[i][j]来代表从起点到顶点i的最短距离剩下j钱，也是合情合理的。这样问题就被规约到普通的寻找路径的算法了。在每一步中我们找到没有标记的状态(i,j)，然后我们将其标记为已访问过(后面将不再使用)，对每个邻居结点，我们查看是否到它的最短距离可以更新。这个方案将会由记录最小值的Min[N-1][j]来表示(状态中具有相同值的最大的j，也就是最短路径的距离一样)。

伪代码:

Set states(i,j) as unvisited for all (i,j)
Set Min[i][j] to Infinity for all (i,j)

Min[0][M]=0

While(TRUE)

Among all unvisited states(i,j) find the one for which Min[i][j]
is the smallest. Let this state found be (k,l).

If there wasn't found any state (k,l) for which Min[k][l] is
less than Infinity - exit While loop.

Mark state(k,l) as visited

For All Neighbors p of Vertex k.
   If (l-S[p]>=0 AND
    Min[p][l-S[p]]>Min[k][l]+Dist[k][p])
      Then Min[p][l-S[p]]=Min[k][l]+Dist[k][p]
   i.e.
If for state(i,j) there are enough money left for
going to vertex p (l-S[p] represents the money that
will remain after passing to vertex p), and the
shortest path found for state(p,l-S[p]) is bigger
than [the shortest path found for
state(k,l)] + [distance from vertex k to vertex p)],
then set the shortest path for state(i,j) to be equal
to this sum.
End For

End While

Find the smallest number among Min[N-1][j] (for all j, 0<=j<=M);
if there are more than one such states, then take the one with greater
j. If there are no states(N-1,j) with value less than Infinity - then
such a path doesn't exist.


下面是一些用来练习的TC中的题目：

Advanced

 下面的问题需要非常好的观察才能够将他们规约到动态规划的问题。

Problem StarAdventure - SRM 208 Div 1: 

 给定一个拥有M行，N列的矩阵(N*M)。在每一个格子中有一些苹果，你从矩阵的左上角出发，可以向下或者向右走。你需要到达右下角。然后你需要通过每一步向上走或者向左走回到左上角。回到左上角之后，你需要回头再到右下角。找出你能够收集的最大苹果数。当你经过一个格子的时候-你会收集到其中所有的苹果。条件: 1 < N,M <= 50;每个格子里面的苹果数在0到1000之间(包括0和1000)。


 首先我们会注意到这个问题和经典的问题（在这篇文章的第三节提到的）有点相似，在那个问题中我们只需要从左上走到右下，然后收集尽量多的苹果。如果能将这里的问题规约到那个问题就太好了。
再仔细的读题-我们应该怎样修改才能够使得它能够使用DP来解决呢? 首先我们观察到我们可以将第二条路径(从右下角走到左上角)看作从左上走到右下的一条路径。这个没有什么区别，因为一条从底到上的路线，可以看作相反方向从上到底的路线。通过这种方法，我们得到了三条从上到下的路径。这无疑减少了问题的难度。当两条路径相交时(如下图),我们将称呼这三条路径叫做 左，中，右。




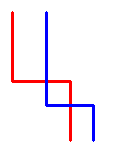
我们可以将他们考虑成下面的图片，而不影响结果:



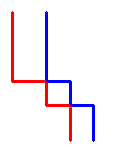
这样我们得到了三条路径，我们将他们考虑为左，中和右。此外，我们还会看到一个最优的方案是不会有相交的地方的(出了左上角和右下角)。因此对于每一行y(除了第一行和最后一行),他们三条线的x坐标分别为x1[y],x2[y]和x3[y]: x1[y]<x2[y]<x3[y]。 在这步做完之后，DP的方案就变得非常明显了。考虑第y行。假定我们已经找到了能够获得最大苹果的路径, x1[y-1],x2[y-1]和x3[y-1]。从他们基础之上，我们找到对于第y行的最优策略。现在我们已经找到了由一行转移到另一行的唯一的方法。设Max[i][j][k]代表在y-1行，并且三条路径的终点在i,j和k能得到的最大苹果数。 对于下一行y行，对于每一个M[i][j][k]加上在单元格(y,i),(y,j)和(y,k)中的苹果数。接着我们继续向下走。在我们移动之后，我们需要考虑到路径可能向右移动了。为了避免出现路径相交的情况。我们首先应该考虑左边路径的右边，然后考虑中间的路径，然后右边的路径。为了更好的理解向右移动，取出每一个可能的对，k(j<k)，对于每一个i(i<j)考虑从位置(i-1,j,k)移动到位置(i,j,k)。左边的路径完成之后，处理中间的，做法类似，最后处理最右边的。


TC中的练习题

附加的注意点:
    当我们阅读完问题之后并着手解决它时，首先看看它的约束条件。如果一个多项式级的算法，那么一个DP的方案是可行的。在这种情况下，试着去找出如果存在一个状态(子问题)，能否推出下一个状态(子问题)。如果发现了之后，应当考虑如何从一个状态转移到另外一个状态。如果它看起来是DP问题，但是你找不出状态，那么试图将其转换为另外一个问题(就像上面第5节的问题一样)。

文中提到的问题:

TCCC '03 Semifinals 3 Div I Easy - ZigZag
TCCC '04 Round 4 Div I Easy - BadNeighbors
TCCC '04 Round 1 Div I Med - FlowerGarden
TCO '03 Semifinals 4 Div I Easy - AvoidRoads
TCCC '03 Round 4 Div I Easy - ChessMetric
TCO '03 Round 4 Div I Med - Jewelry
SRM 150 Div I Med - StripePainter
SRM 197 Div II Hard - QuickSums
SRM 165 Div II Hard - ShortPalindromes
SRM 208 Div I Hard - StarAdventure
SRM 178 Div I Hard - MiniPaint
 

posted @ 2010-12-09 22:46  BuildNewApp  阅读(575)  评论(0)  编辑  收藏  举报