马科维兹资产组合选择模型

组合构造问题可以归纳为多个风险资产和一个无风险资产的情况。在两风险资产的例子中，该问题可分为三步：
首先，确定可行集的风险收益权衡；
然后，通过计算使资本配置线斜率最大的个资产权重权重确定最优风险组合；
最后确认最合适的投资组合，由无风险资产和最优风险组合构成。
投资者面临的风险收益机会，由风险资产的最小方差边界(\(minimum-variance \; frontier\))给出。该边界线是由给定组合期望收益下方差最低的组合点描绘的曲线，在给定期望收益、方差和协方差数据，描绘的图如下图所示：

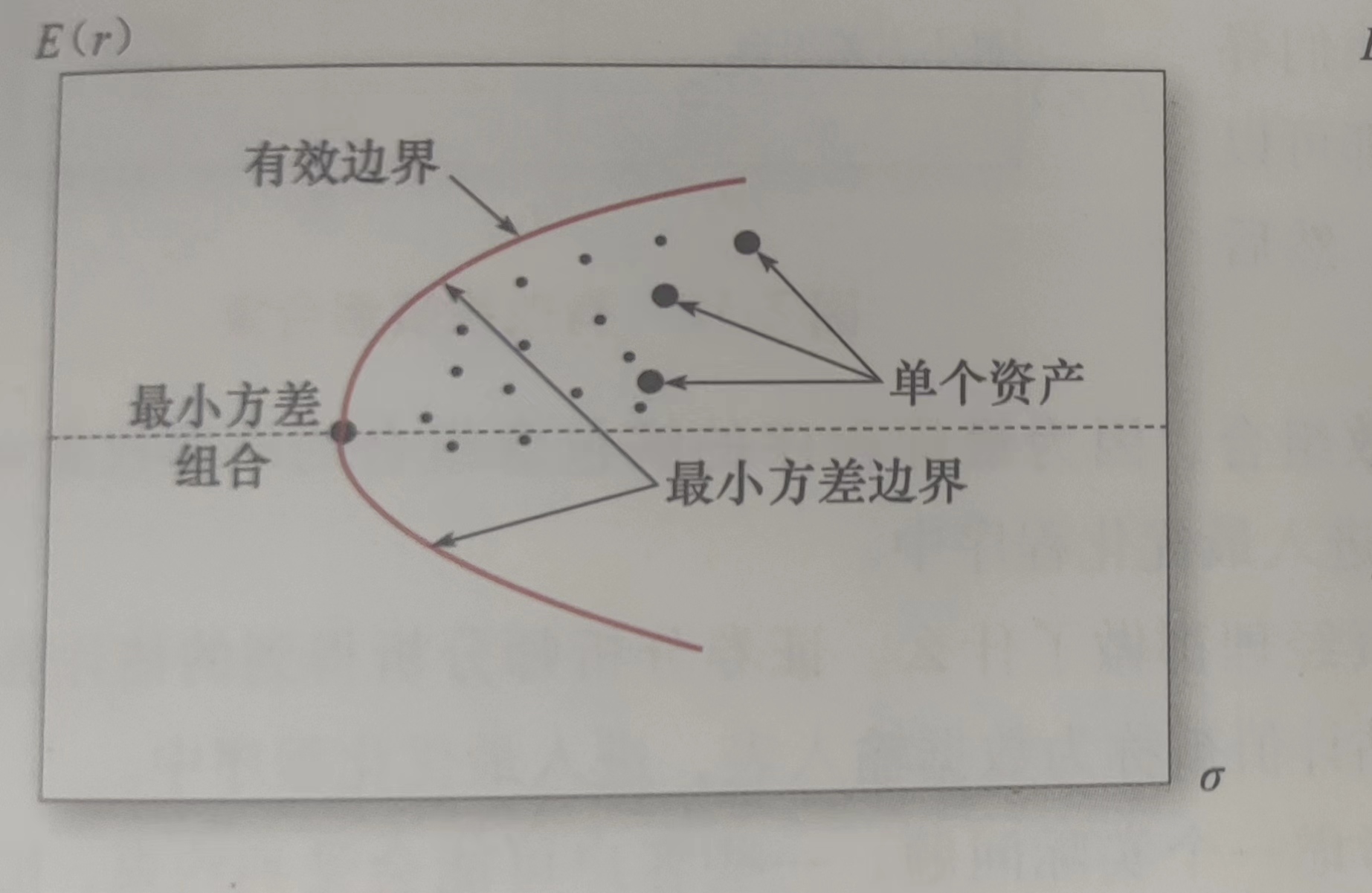
可以注意到所有单个资产都在有效边界右侧，至少在存在卖空机制时是这样的（当不存在卖空机制时，同等风险下，最高收益的证券一定在有效边界上，有效边界上的证券，在同等收益时，方差是最小的。当存在卖空机制时，可以通过卖空低收益、买进高收益证券的方式构建出更高收益或更低波动性的更优组合）。说明由单个资产构成的风险组合不是最有效的，分散化投资可以提升期望收益降低风险。
所有最小方差边界上最小方差组合上方的点提供最优的风险和收益，因此可以作为最优组合，这一部分被称为风险资产有效边界(\(efficient \; frontier \; of \; risky \; assets\))。对于最小方差点下的组合，其正上方就存在具有相同标准差但期望收益更高的组合。报酬-波动比率最高的资本配置线如下图所示：

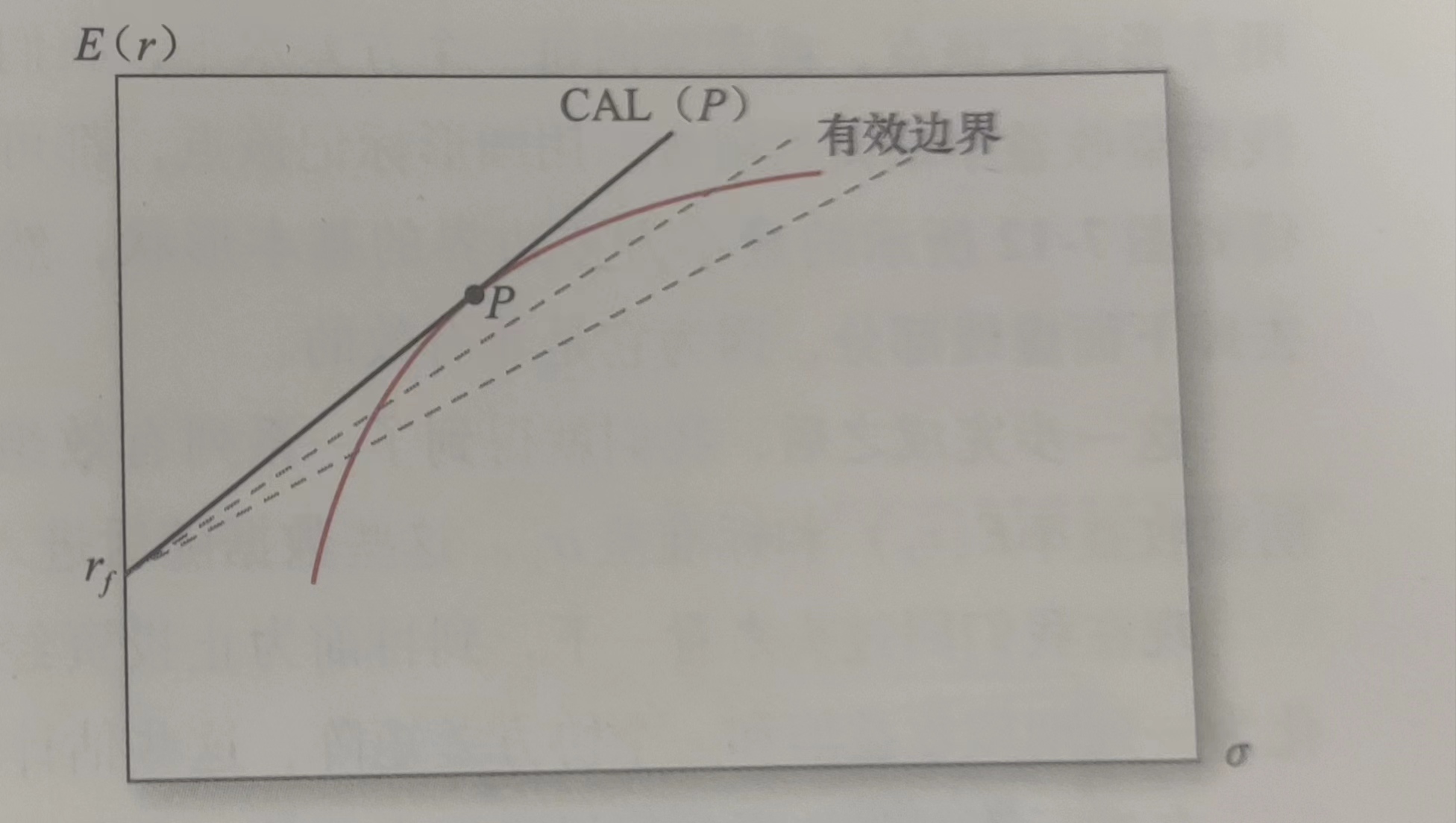
该条资本配置线与有效边界相切，切点是最优风险组合\(P\)。
最后一步是投资者在最优风险资产\(P\)和短期国库券之间选择合适的比例构成的最终组合，如下图所示：

进一步考虑构造组合的每一步细节，第一步中，风险收益分析，投资经理需要每个证券的期望收益率和标准差、写证券之间的协方差矩阵的估计值。投资经理现在有\(E(R_i)\)和\(n*n\)的协方差矩阵，矩阵对角线是\(n\)个\({\sigma_i}^2\)，其余是\(n^2-n=n(n-1)\)个协方差值，关于对角线对称，因此只有一半的值需要估计。如果有50支证券需要进行组合管理，需要\(50\)个期望收益，\(50\)个标准差，\(50*(49/2)\)个协方差。
一旦这些估计完成，任意风险组合（各资产权重为\(w_i\)）的期望收益和方差都可以通过协方差矩阵或通过下式延申公式计算得到：

\[E(r_p)=\sum_{i=1}^n w_i*E(r_i) \]

\[{\sigma_p}^2=\sum_{i=1}^n \sum_{j=1}^n w_i*w_j*Cov(r_i,r_j) \]

风险资产组合边界背后的核心原理是，对于任意风险水平，我们只关注期望收益率最高的组合，或者说，边界是给定期望收益风险的最小组合集。