算法题-最长回文子串-动态规划

 

动态规划方法---解题思路

1. 定义dp[i][j] 容器，其中i, j表示为字符串中i到j的子串，是否为回文

2. dp初始化

     2.1 dp[i][i] = true;

     2.2 if s[i] == s[i+1] 则 dp[i][i+1] = true；

3. 状态转移方程：如果dp[i+1][j-1] == true && s[i] == s[j] 则 dp[i][j] == true;

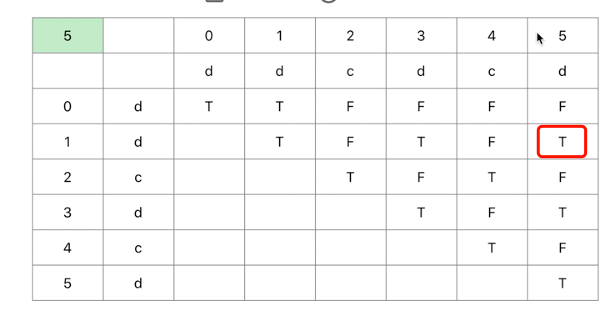
下图为具体dp实现过程

 

代码如下

class Solution {
public:
    string longestPalindrome(string s) {
        int len=s.size();
        if(len==0||len==1)
            return s;
        int start=0;//回文串起始位置
        int max=1;//回文串最大长度
        vector<vector<int>>  dp(len,vector<int>(len));//定义二维动态数组
        for(int i=0;i<len;i++)//初始化状态
        {
            dp[i][i]=1;
            if(i<len-1&&s[i]==s[i+1])
            {
                dp[i][i+1]=1;
                max=2;
                start=i;
            }
        }
        for(int l=3;l<=len;l++)//l表示检索的子串长度，等于3表示先检索长度为3的子串
        {
            for(int i=0;i+l-1<len;i++)
            {
                int j=l+i-1;//终止字符位置
                if(s[i]==s[j]&&dp[i+1][j-1]==1)//状态转移
                {
                    dp[i][j]=1;
                    start=i;
                    max=l;
                }
            }
        }
        return s.substr(start,max);//获取最长回文子串
    }
};