常见查找算法

常见的查找主要有：

1：顺序查找

2：二分查找

3：分块查找

4：哈希查找

5：斐波那契查找

6：树表查找

7：插值查找

主要介绍一下在牛客网做题常碰见的四种查找方法。

1.顺序查找：

顺序查找：顺序查找适合于存储结构为顺序存储或链接存储的线性表

复杂度分析：　
　　平均查找长度为（n+1）/2 最好1 最坏n
　　时间复杂度为O(n)

       平均时间为 n/2

       

2.二分查找：

二分查找：二分查找的数组必须是有序的，每次将需要查找的数据与中间的数据进行比较，不断缩小查找范围，最终查找到合适的位置。其中表必须有序且只能以顺序的方式进行存储。（二分查找后，对不符合的标号，不要移动指针即 I=middle+1或j=middle-1）

复杂度分析：

         最坏条件下，关键词比较次数为log2（n）+1,向下取整

         时间复杂度为O(logn)。

如何求二分查找的平均查询长度：例题：具有12个关键字的有序表，折半查找的平均查找长度为多少？O(log₂(n))

画出判定树如下

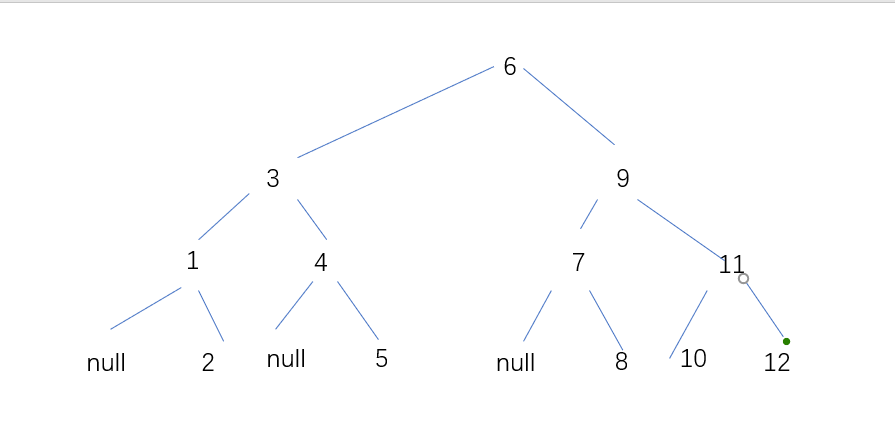
第一层长度为1以此递推，（1*1+2*2+3*4+5*4）=37/12

 

3.分块查找：

分块查找：分块查找是折半查找和顺序查找的一种改进方法，分块查找由于只要求索引表是有序的，对块内节点没有排序要求，因此特别适合于节点动态变化的情况。

4 hash查找

哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制，那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1)；如果没有时间限制，那么我们可以使用无序数组并进行顺序查找，这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。

其中为了提高散列的查找效率，可以采用设计冲突少的散列函数与处理冲突时避免产生聚集（堆积的现象）。

面试常见题：分块查找，hash查找，折半查找，顺序查找，按照最差时间复杂度排序为：顺序查找，分块查找，二分查找，hash查找。