两条线段相交判断学习理解

两条线段相交判断可以分为两步：

1,快速排斥实验

2,跨立实验

详细解释：

第一步检查以线段A为对角线的矩形和以线段B对角线的矩形是否相交，如果不相交则两条线段必然不相交，可以快速排除，如果相交就继续检查是否有交点；

所以第一步也叫做快速排斥实验，首先先进行第一步的研究：

      

如果知道，如果cd边的最大点的x值小于ab边的最小点的x值 ,或者cd边最大点的y值小于ab边的最小点的y值可以说明分别以两线段为对角线的矩形不相交；

代码表示如下:

max(C.x,D.x)<min(A.x,B.x)或者max(C.y,D.y)<min(A.y,B.y)

同样也需要检查上面的边的代号反过来的：

max(A.x,B.x)<min(C.x,D.x)或者max(A.y,B.y)<min(C.y,C.y)

如果上面的四条判断有一个为真，则代表两线段必不可交，否则应该进行第二步判断；

当通过第一步后会有下面四种可能：

跨立实验：

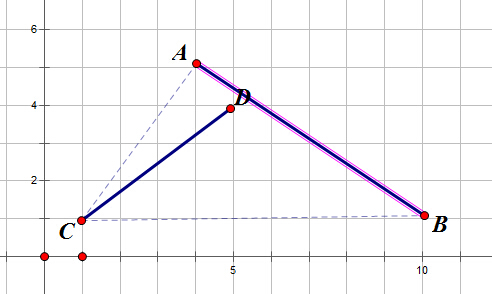
如果两线段相交那么就意味着它们互相跨立，即如上图点A和B分别在线段CD两侧，点C和D分别在线AB两侧。

即向量(A-C)和(B-C)分别在向量(D-C)两边，则向量(A-C)和(D-C)的叉乘积与(B-C)和(D-C)的叉乘积符号相反，根据右手定则，它们的叉乘积方向一个向下一个向上，是方向相反的

平行线。则它们的点乘小于零。如果向量(A-C)和(B-C)在向量(D-C)同一侧，则它们叉乘积同向，因为根据右手定则都向一个方向指向，所以它们是符号相同的平行线，即点乘大于零；

公式是：

（(A-C)x(D-C))*((B-C)x(D-C))<0;

同样需要证明向量(D-B)和向量(C-B)在向量(A-B)的两侧，（(D-B)x(A-B))*((C-B)x(A-B))<0;这两个同时成立才行；

但是对于中间那个图，则不满足上面的两个公式了，它也是成立的；此时公式中该如何表达呢？

即当（(A-C)x(D-C))*((B-C)x(D-C))=0 或者（(D-B)x(A-B))*((C-B)x(A-B))=0时，下面给出行证明当这两个公式等于零时为中间那个图的情形

如果等于零，那么代表公式(A-C)x(D-C)或者(B-C)x(D-C)等于0，（它两个不可能垂直在）；

即（A-C）和(D-C)可能共线或者（B-C）和（D-C）可能共线，（或者另外两对里面出现共线的），这样他们就一定会是相交的。