KMP 算法
前缀函数
定义
定义字符串 \(s\) 和它的长度 \(n\),字符串 \(s\) 可以写作 \(s_0s_1s_2s_3...s_n\)
定义真前缀为:从 \(s\) 的首部开始到某个位置 \(i\) 结束的子串,但不包括 \(s\) 本身
定义真后缀为:从 \(s\) 的某个位置 \(i\) 开始到 \(s\) 的尾部结束的子串,但不包括 \(s\) 本身
定义 \(s\) 的前缀函数为:\(\pi(i)\) 为 \(s_0 ... s_i\) 中最长的相同前后缀长度
递推
递推基础:\(\pi(0) = 0\)
证明:因为真前缀/真后缀不包括串本身,长度为\(1\)的子串\(s_0\)不存在真前缀/真后缀,所以长度显然是 \(0\),前缀函数的值也是 \(0\)
递推步骤:对于每个 \(i > 0\),比较\(s_{\pi(i-1)}\)和\(s_i\)
-
如果\(s_{\pi(i-1)}=s_i\),那么\(\pi(i) = \pi(i-1) + 1\)
-
如果\(s_{\pi(i-1)}\neq s_i\),那么再次比较\(s_i\)和\(s_{\pi(\pi(i-1)-1)}\),重复这个递推步骤,直到\(\pi...(\pi(\pi(i-1)-1)) = 0\)仍然不相同,那么\(\pi(i) = 0\)
证明:
-
首先考虑求出\(\pi(i-1)\)的时候发生了什么:我们得到 \(s_0...s_{\pi(i-1)-1} = s_{i-\pi(i-1)}...s_{i-1}\),等式左部是真前缀,等式右部是真后缀。那么既然\(s_{\pi(i-1)}=s_i\)的话,我们可以把真前缀和真后缀都往前推进一步,得到:\(s_0...s_{\pi(i-1)-1}s_{\pi(i-1)} = s_{i-\pi(i-1)}...s_{i-1}s_i\),所以\(\pi(i) = \pi(i-1) + 1\)
图示:

-
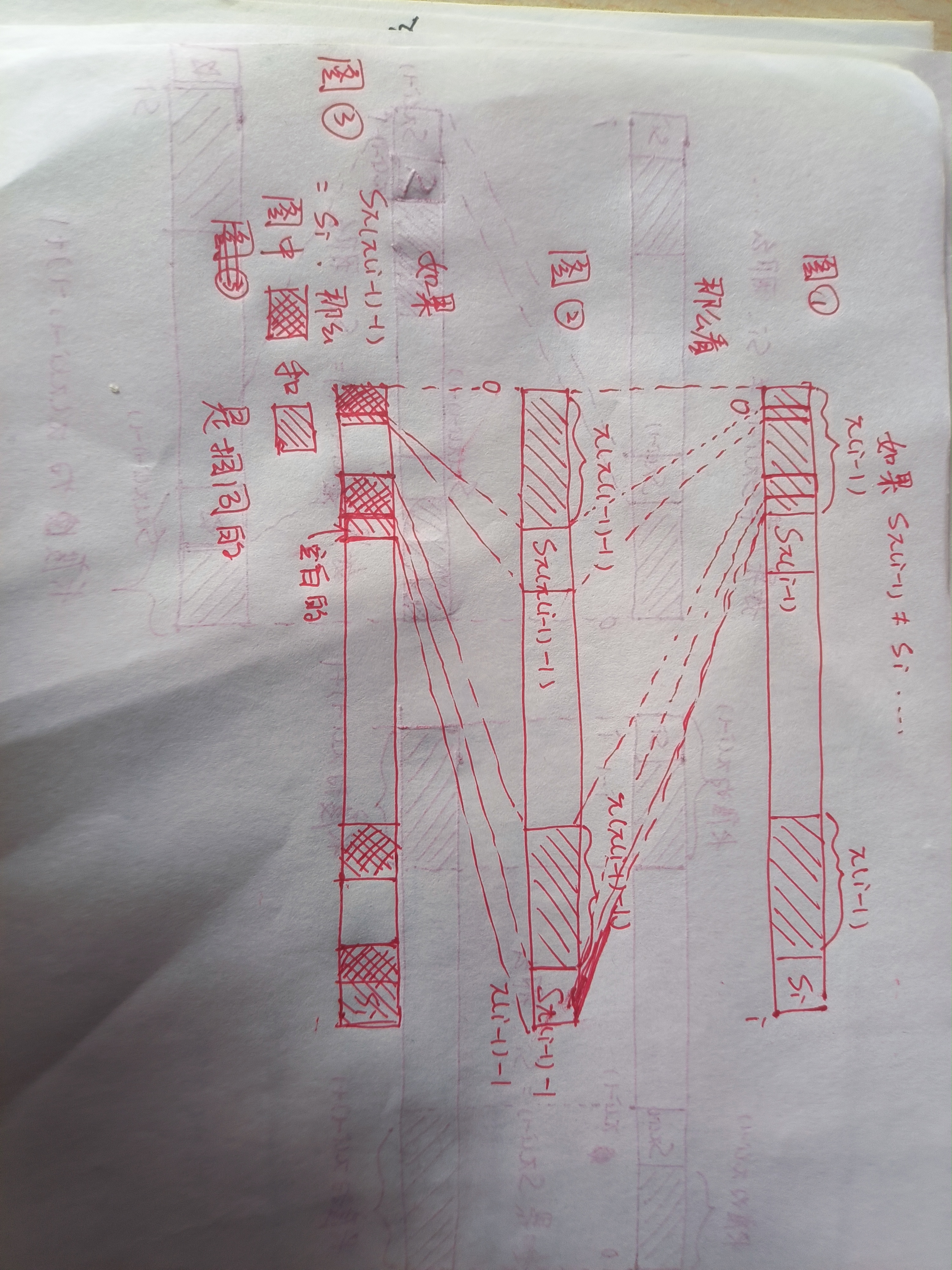
\(s_{\pi(i-1)}\neq s_i\) 会稍微麻烦一些,因为这意味着我们已经没法使用\(s_0...s_{\pi(i-1)-1} = s_{i-\pi(i-1)}...s_{i-1}\)来推进了,我们需要尝试更短的真前缀/真后缀。容易发现,找更短的真前缀/真后缀的过程和当前问题的结构是一样的,我们可以利用前缀函数 \(\pi(\pi(i-1)-1)\) 以及其对应的真前缀/真后缀 \(s_0...s_{\pi(\pi(i-1)-1)-1} = s_{\pi(i-1)-\pi(\pi(i-1)-1)}...s_{\pi(i-1)-1}\)。如果我们运气很好,找到了\(s_i = s_{\pi(\pi(i-1)-1)}\),那么有如下的推理:
因为 \(\pi(\pi(i-1)-1)\) 有:$$s_0...s_{\pi(\pi(i-1)-1)-1} = s_{\pi(i-1)-\pi(\pi(i-1)-1)}...s_{\pi(i-1)-1} ①$$
又因为 \(\pi(i-1)\) 有:$$s_0...s_{\pi(i-1)-1} = s_{i-\pi(i-1)}...s_{i-1}②$$
可以观察到式子\(①\)等号左部和右部都是式子\(②\)的等号左部的一部分,那么你可以在式子\(②\)的等号右部截取同样长的一个后缀,使得下面这个等式仍然成立(一种传递性):$$s_0...s_{\pi(\pi(i-1)-1)-1} = s_{i-\pi(\pi(i-1)-1)}...s_{i-1}$$
又因为\(s_i = s_{\pi(\pi(i-1)-1)}\),所以$$s_0...s_{\pi(\pi(i-1)-1)-1}s_{\pi(\pi(i-1)-1)} = s_{i-\pi(\pi(i-1)-1)}...s_{i-1}s_i$$
这意味着我们可以推进一步,否则就递归的进行这个过程。
图示:
KMP 算法
KMP 算法被用来高效地解决子串匹配问题:在一个很长的字符串 \(s\)(下面我们简称为母串)中查询是否有子串 \(p\) 出现,比如判定子串hello出现在helloworld中。KMP 算法的核心思想就是用上面定义的前缀函数减少匹配次数。
传统暴力
传统暴力的思路非常简单:枚举子串在母串中的起始位置,对于一个可能的起始位置,依次检查字符是否相同,如果不同,那么推进到下一个起始位置。
for (int i = 0; i < s.length(); i++)
for(int j = 0; l < p.length(); j++) {
if (s[i] != p[j]) break;
if (j == p.length() - 1) printf("Find at %d", i);
}
假设母串和子串的长度分别是 \(n\) 和 \(m\),算法复杂度显然是 \(O(n*m)\) 的
KMP 算法
KMP 算法利用前缀和后缀来避免不必要的比较。假设我们有母串 aaaaaaba 和子串 aaab:
假设我们已经枚举到母串中 \(i = 2\) 的位置,在检查中发现母串中 \(i = 5\) 和子串中 \(j = 3\) 的位置符号不相同(简称为失配)。那么在下一步,我们有必要从母串中 \(i = 3\) 的位置开始吗?
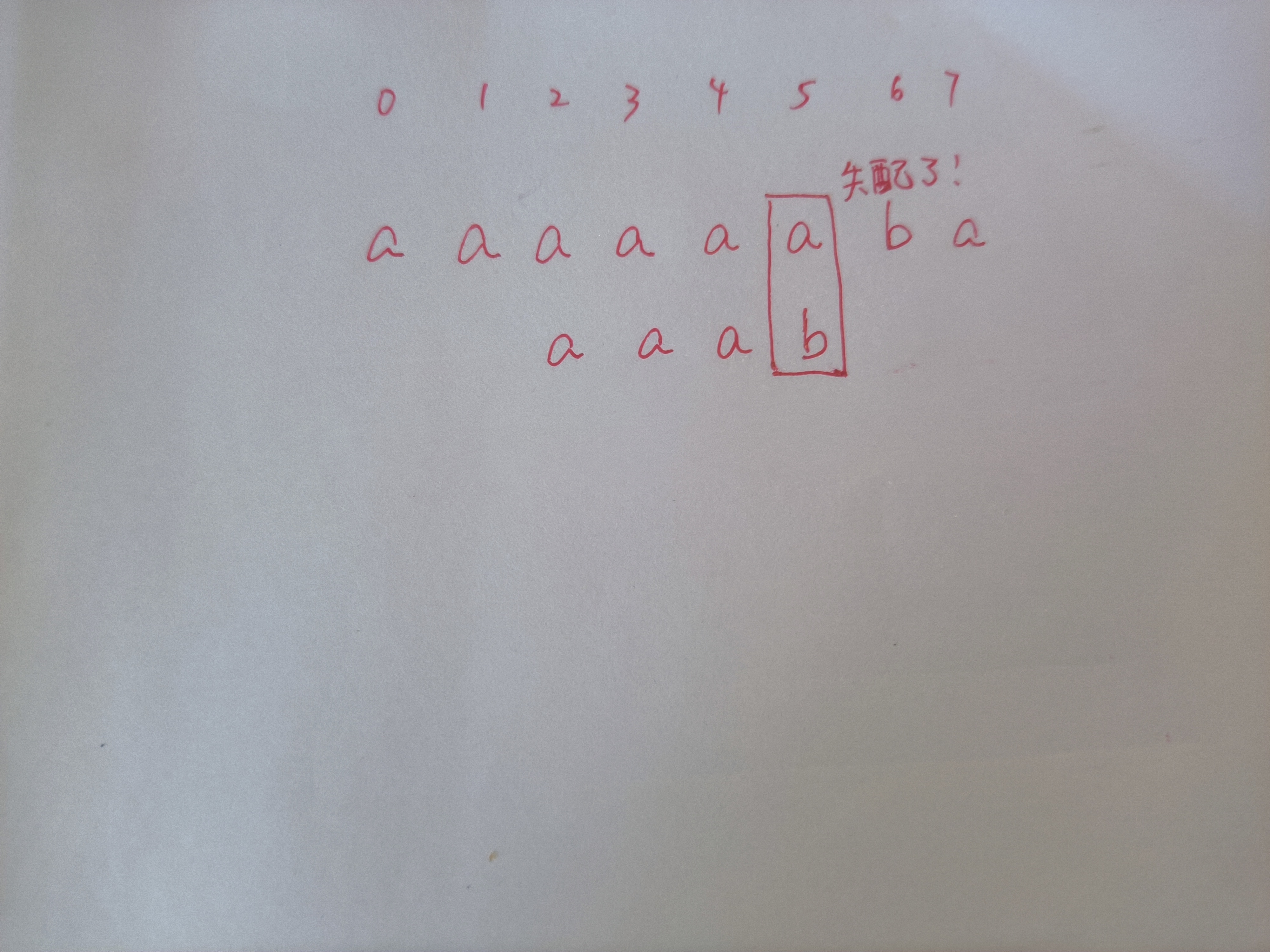
既然都这么问了,肯定不需要。因为母串中的 \(i = 2, 3, 4\) 和子串中的 \(j = 0, 1, 2\) 已经匹配上了,也就是 \(s_2s_3s_4 = p_0p_1p_2\)。经历过上面前缀函数的磨练,你也能发现对于子串来说 \(\pi(2) = 2\),那么 \(p_0p_1 = p_1p_2\),那么显然有 \(p_0p_1 = s_3s_4\)(和上面前缀函数相似的“传递”)。这意味着在下一个起始位置:母串中的\(i = 3\),我们不再需要检查\(s_3s_4\)是否等于\(p_0p_1\),直接检查\(s_5\)和\(p_2\)是否相同。显然,这么做节省了很多步骤。
让我们尝试把情况泛化:
假设在母串的位置 \(i\) 和子串的位置 \(j\) 发生了失配,即\(s_i \neq p_j\):
-
\(j \neq 0\),那么下一个要比较 \(s_i\) 和 \(p_{\pi(j-1)}\)
-
\(j = 0\),应该枚举母串的下一个位置 \(i\)
如果没有失配,那么同时推进 \(i\) 和 \(j\)。
证明:TBD
#include<bits/stdc++.h>
using namespace std;
string s1, s2;
#define maxn 2000010
int nxt[maxn];
int main() {
cin >> s1 >> s2;
memset(nxt, 0, sizeof(nxt));
for (int i = 1; i < s2.size(); i++) {
if (s2[i] == s2[nxt[i - 1]]) {
nxt[i] = nxt[i - 1] + 1;
} else {
int j = nxt[i - 1];
while (j > 0 && s2[i] != s2[j]) j = nxt[j - 1];
if (s2[i] == s2[j]) j++;
nxt[i] = j;
}
}
int j = 0;
for (int i = 0; i < s1.size(); i++) {
while (j > 0 && s1[i] != s2[j]) j = nxt[j - 1];
if (s2[j] == s1[i]) j++;
if (j >= s2.size()) {
printf("%d\n", i - s2.size() + 2);
j = nxt[j - 1];
}
}
for (int i = 0; i < s2.size(); i++) {
printf("%d ", nxt[i]);
}
return 0;
}
复杂度分析
KMP 的计算复杂度是 \(O(n + m)\)
证明:
TBD



 浙公网安备 33010602011771号
浙公网安备 33010602011771号