一小时速通计组

计算机组成与设计课程复习

与 CSAPP 中类似的部分做了忽略或者简化

性能的度量

知识回顾

七个伟大思想：

1. 利用抽象简化设计

2. 加速经常性事件

3. 通过并行提高性能

4. 通过流水线提高性能

5. 通过预测提高性能

6. 存储层次

7. 通过冗余提高可靠性

对于某个计算机 X，定义性能和执行时间的关系表达式：

\[\text{性能}_X = \frac{1}{\text{执行时间}_X} \]

描述时钟周期和时钟频率的关系：

\[\text{时钟周期} = \frac{1}{\text{时钟频率}} \]

对于某个程序，CPU执行时间的计算公式：

\[ \text{CPU执行时间} = \text{CPU时钟周期数} \times \text{时钟周期} \\ = \text{CPU时钟周期数} \times \frac{1}{\text{时钟频率}} \]

指令平均时钟周期数

\[\text{CPI} = \frac{\text{CPU时钟周期数}}{\text{指令数}} \]

基本性能公式

\[\text{CPU执行时间} = \text{CPI} \times \text{指令数} \times \text{时钟周期} = \frac{\text{CPI} \times \text{指令数}}{\text{时钟频率}} \]

SPEC 分值

\[\text{SPEC}_X = \frac{\text{基准测试程序在 X 上的执行时间}}{\text{基准测试程序在标准机器上的执行时间}} \]

课后练习

解答思路：

a. $ \text{时钟周期} = \frac{1}{\text{时钟频率}} $

$ \text{每秒执行的指令数} = \frac{1}{{\text{时钟周期}}\times{\text{CPI}}} $

b. $ \text{时钟周期数} = \text{时钟频率} \times \text{CPU执行时间} $

$ \text{指令数} = \frac{\text{时钟周期数}}{\text{CPI}} $

c. $ \text{时钟频率} = \frac{1}{\text{时钟周期}} = \frac{CPI \times \text{指令数}}{\text{CPU执行时间}} $

解答思路：

a. $ \text{整体CPI} = \Sigma \text{CPI}_i \times \text{比例}_i $

b. $\text{时钟周期总数} = \text{整体CPI} \times \text{指令总数} $

RISC-V 指令集

知识回顾

1. 简单即规整

2. 更少即更快

存储程序概念

lui 指令：取左移 12 位后的 20 位立即数，目的是给一个寄存器赋一个 32 位的值；比如：将 0x12345678 放入 x19

lui x19, 0x12345
addi x19, x19, 0x678

通过使用 x0 寄存器，跳转-链接指令也可以实现无条件跳转

jal x0, 0x1000

在 RISC-V 中，栈指针是寄存器 x2，也称为 sp；按照历史惯例，栈按照从高到低的方向增长

x5 ~ x7, x28 ~ x31：caller-saved 寄存器，称为临时寄存器 t0 ~ t6 (temporary)

x8 ~ x9, x18 ~ x27：callee-saved 寄存器，称为保存寄存器 s0 ~ s11 (saved)

x10 ~ x17：参数寄存器 a0 ~ a7 (argument)

x10 ~ x11：返回值寄存器 a0 ~ a1

x1：返回地址寄存器 也称 ra (return address)

关于 RISC-V 对过程的支持，以递归实现的阶乘函数为例：

观察栈的变化以及 x1 的使用

RISC-V 的内存（memory）存储模型

一些 RISC-V 编译器使用帧指针 fp (frame pointer) 或者寄存器 x8 来指向过程帧（在一个过程中存储在栈上的寄存器或者局部变量，也称活动记录）的第一个字（实际上就是保存了一个地址）

保留加载字（lr.w）和条件存储字（sc.w）指令，用于实现原子操作；这两个指令按序使用，如果保留加载指令指定的内存位置的内容在条件存储指令执行到同一地址前发生了变化，则条件存储指令失败且不会把数据写回内存。这是一种指令对的方法，用于实现原子（atomic）操作（在两个操作之间不能插入其他操作，就像原子不可分一样）。

比如，实现一个原子交换（atomic swap）操作：

again: lr.w x10, (x20)
       sc.w x11, x23, (x20)
       bne x11, x0, again
       addi x23, x10, 0

lr.w 做了两件事：1. 从 x20 指向的内存位置读取一个字到 x10；2. 把 x20 指向的内存位置设置保留标记

sc.w 在把 x23 写进 x20 指向的内存位置之前，先判断 x20 指向的内存位置有没有设置保留标记，如果有，写入成功，x11 被设置为 0；如果没有，写入失败，x11 被设置为 1；无论成功与否，x20 指向的内存位置的保留标记都会被 sc 清除

指路

在第二个例子中，x20 指向了一个锁

课后习题

addi x12, x30, 8 // x12 = &A[f+1]
ld x30, 0(x12) // x30 = A[f+1]
add x30, x30, x5 // x30 = A[f+1] + A[f]
sd x30, 0(x31) // B[g] = A[f+1] + A[f]

addi x5, x0, x0 // x5 = 0
slli x5, x28, 3 // x5 = i * 8
add x5, x5, x10 // x5 = &A[i]
addi x6, x0, x0 // x6 = 0
slli x6, x29, 3 // x6 = j * 8
add x6, x6, x11 // x6 = &B[j]
ld x7, 0(x5) // x7 = A[i]
ld x5, 0(x6) // x5 = B[j]
add x5, x5, x7 // x5 = A[i] + B[j]
sd x5, 64(x11) // B[8] = A[i] + B[j]

我们用 Compile Explorer 做一下

int square(int A[], int B[], int i, int j) {
    B[8] = A[i] + B[j];
}

编译结果是

square(int*, int*, int, int):
        addi    sp,sp,-32 // 保存用到的 saved 寄存器
        sw      ra,28(sp) // 保存 ra 寄存器 (x1)
        sw      s0,24(sp) // 保存 s0 寄存器 (x8)
        addi    s0,sp,32 // x8 = sp + 32 过程帧寄存器 (fp)
        sw      a0,-20(s0) // 保存 &A[0]
        sw      a1,-24(s0) // 保存 &B[0]
        sw      a2,-28(s0) // 保存 i
        sw      a3,-32(s0) // 保存 j
        lw      a5,-28(s0) // a5 = i
        slli    a5,a5,2 // a5 = i * 4
        lw      a4,-20(s0) // a4 = &A[0]
        add     a5,a4,a5 // a5 = &A[i]
        lw      a3,0(a5) // a3 = A[i]
        lw      a5,-32(s0) // a5 = j
        slli    a5,a5,2 // a5 = j * 4
        lw      a4,-24(s0) // a4 = &B[0]
        add     a5,a4,a5 // a5 = &B[j]
        lw      a4,0(a5) // a4 = B[j]
        lw      a5,-24(s0)// a5 = &B[0]
        addi    a5,a5,32 // a5 = &B[8]
        add     a4,a3,a4 // a4 = A[i] + B[j]
        sw      a4,0(a5) // B[8] = A[i] + B[j]
        ebreak // 退出

发现编译器选择使用 fp 作为基地址

观察 jal 和 jalr 分配给立即数的位数即可

同样，使用 Compile Explorer 做个小实验

int g (int a, int b);

int f (int a, int b, int c, int d) {
    return g(g(a, b), c + d);
}

编译结果是

f(int, int, int, int):
        addi    sp,sp,-32 // 保存现场
        sw      ra,28(sp) // 保存 ra
        sw      s0,24(sp) // 保存 s0
        addi    s0,sp,32 // s0 = sp + 32 过程帧寄存器
        sw      a0,-20(s0) // 保存 a0
        sw      a1,-24(s0) // 保存 a1
        sw      a2,-28(s0) // 保存 a2
        sw      a3,-32(s0) // 保存 a3
        lw      a1,-24(s0) // a1 = b
        lw      a0,-20(s0) // a0 = a
        call    g(int, int) // g(a, b)
        mv      a3,a0 // a3 = g(a, b)
        lw      a4,-28(s0) // a4 = c
        lw      a5,-32(s0) // a5 = d
        add     a5,a4,a5 // a5 = c + d
        mv      a1,a5 // a1 = c + d
        mv      a0,a3 // a0 = g(a, b)
        call    g(int, int) // g(g(a, b), c + d)
        mv      a5,a0 // a5 = g(g(a, b), c + d)
        mv      a0,a5 // 返回值
        lw      ra,28(sp) // 恢复现场
        lw      s0,24(sp)
        addi    sp,sp,32
        jr      ra

这里的 mv 应该是 RISC-V 的伪指令

总结一下：保存现场（使用的 saved 寄存器、过程帧寄存器） -> 执行函数调用 -> 恢复现场

计算机的算术运算

知识回顾

串行乘法：模拟手工执行的乘法运算

人类是这么进行手工运算的：

实际上，对于乘数的每一位，如果是 1，就把被乘数加到结果对应的位上（具体表现为左移）；如果是 0，就不加

那么可以自然而然地设计出如下串行乘法器

左边是控制单元，右边是数据通路

如果每个步骤花费一个时间周期，那么执行一个三十二位乘法需要将近一百个时间周期，这在时间上的花费是巨大的；时间上的优化考虑并行，对被乘数和乘数的移位可以并行执行；空间上的优化有点意思，观察到 Product 寄存器一开始的右三十二位没有被使用，执行一轮后是右三十一位，以此类推，而乘数寄存器在乘法结束时右三十二位也没有被使用，在倒数第二轮乘法结束时右三十一位没有被使用，那么可以考虑将二者合并，共用一个六十四位寄存器

更高的集成度使得我们可以用更多的加法器来并行执行乘法，下面是一个快速乘法器硬件图：

每一层的加法器都可以并行执行，这样可以大大减少乘法的时间开销，达到 log(n) 的时间复杂度

除法不考 😋 浮点表示参考 CSAPP 中关于 IEEE754 的部分

ALU的设计：很容易设计一个 1-Bit 的加法器（3 个输入，2 个输出）

串联起来，可以得到一个 32-Bit 行波进位加法器

如果我们把这个 1-Bit 的加法器扩展：减法、与、或，那么就要引入控制位 invert 和 operation；注意，对于理想中的 \(a-b\) 实际上得到 \(a+\overline{b}\)，想要得到真正的减法结果，需要把 carry-in 设为 1

还需要支持 slt 指令，slt rd, rs1, rs2 的意思是如果 rs1 < rs2，则 rd = 1，否则 rd = 0

新增了一条 set 线路，用于把结果放入 result0，这样的话，如果 rs1 < rs2，那么 result = 0000...0001，否则 result = 0000...0000

还需要支持 beq 指令，这个比较简单，加入一个或门判断是否为全 0 即可

这样，我们就得到了一个简化的 ALU，用 Verilog 描述如下

module ALU(
    input [3:0] ctrl,
    input [31:0] A,B;
    output [31:0] result;
    output zero;
);
    assign zero = (result == 32'b0);
    always @(*) begin
        case(ctrl)
            4'b0000: result = A + B;
            4'b0001: result = A - B;
            4'b0010: result = A & B;
            4'b0011: result = A | B;
            4'b0100: result = A < B ? 32'b1 : 32'b0;
            default: result = 32'b0;
        endcase
    end
endmodule

在后面的单周期 CPU 设计中，会有完整版本的 ALU

课后习题

实现一个支持六种运算的 ALU

// 32-Bit ALU with 6 operations
module alu (
  A, B, ALUOp, // Inputs
  C // Output
);

input[31:0] A, B; // rs1, rs2
input[2:0] ALUOp; // op
output reg[31:0] C; // res

always @(*) begin
  case(ALUOp)
    // unsigned addition
    3'b000: C = A + B;
    // unsigned subtraction
    3'b001: C = A - B;
    // and
    3'b010: C = A & B;
    // or
    3'b011: C = A | B;
    // logical right-shift
    3'b100: C = A >> B;
    // arithmetic right-shift
    3'b101: C = ($signed(A)) >>> B;
    // unsigned greater
    3'b110: C = (A > B) ? 1 : 0;
    // signed greater
    3'b111: 
      begin
        if (A[31] == 0 && B[31] == 1) C = 1;
        else if (A[31] == 1 && B[31] == 0) C = 0;
        else C = (A > B) ? 1 : 0; // 好像没必要这么做？
      end
  endcase
end  
endmodule

单周期 CPU

知识回顾

这一部分实现的单周期 CPU 支持 7 条指令 lw, sw, add, sub, and, or, beq

程序的执行可以粗略划分为：1. 取指 2. 执行 两个大阶段

逻辑设计方法：

RISC-V 中实现的数据通路包含两种不同类型的逻辑单元：组合逻辑单元（处理数据值的单元）和状态单元（存储状态的单元）；组合逻辑单元的输出仅依赖于当前输入，给定相同的输入，产生相同的输出，输入变化了输出也立即发生变化；状态单元有内部存储功能，至少有两个输入（写入的数据和时钟信号）和一个输出（前一个周期写入的数据）；包含状态的逻辑部件也称为时序的，输出取决于输入和状态

单周期 CPU 采用时钟边沿触发

和之前的 RISC-V 指令集保持一致，处理器处理的数据宽度为 32 位

COD 书上介绍了如何从具体的功能模块抽象成独立的逻辑单元，这里不再赘述；

几乎每个单元都有一个控制信号，用于控制这个单元的工作；理想的解决方案是设计一个单元，通过指令的操作码（funct opcode）可以产生所有的控制信号，这个单元称为控制单元

对于 R 型指令，数据通路可以描述为：

从 Im 里面取指 -> Control 产生控制信号（RegWrite = 1, ALUSrc = 0, MemtoReg = 0, MemWrite = 0, MemRead = 0, Branch = 0） -> 从 RegFile 读取 rs1, rs2 -> ALU 计算 -> 结果写回 RegFile -> PC + 4

对于 I 型指令中的计算指令（比如 addi），数据通路可以描述为：

从 Im 里面取指 -> Control 产生控制信号（RegWrite = 1, ALUSrc = 1, MemtoReg = 0, MemWrite = 0, MemRead = 0, Branch = 0） -> 从 RegFile 读取 rs1 -> 立即数产生单元产生立即数 -> ALU 计算 -> 结果写回 RegFile -> PC + 4

对于 I 型指令中的访存指令（比如 lw），数据通路可以描述为：

从 Im 里面取指 -> Control 产生控制信号（RegWrite = 1, ALUSrc = 1, MemtoReg = 1, MemWrite = 0, MemRead = 1, Branch = 0） -> 从 RegFile 读取 rs1 -> 立即数产生单元产生立即数 -> ALU 计算 -> 访存 -> 结果写回 RegFile -> PC + 4

对于 S 型指令，数据通路可以描述为：

从 Im 里面取指 -> Control 产生控制信号（RegWrite = 0, ALUSrc = 1, MemtoReg = 0, MemWrite = 1, MemRead = 0, Branch = 0） -> 从 RegFile 读取 rs1 -> 立即数产生单元产生立即数 -> ALU 计算 -> 把 ReadData2 读出来的写进Memory中对应ALU计算结果的地址 -> PC + 4

有意思的一点是，只有通过这个数据通路，才能完全理解为什么 sw 和 lw 在汇编中长相相同，对应的 32 位指令却不同：lw 和 sw 的写入目标不同，一方面要满足简单即规整的设计原则，是 rs1 rs2 rd 字段位置一致，另一方面还要满足数据通路的设计要求，如果 ReadData1 读出来的是要写入的数据，这个通路就不能运行了

“简单即规整”！

对于 SB 型指令，数据通路可以描述为：

从 Im 里面取指 -> Control 产生控制信号（RegWrite = 0, ALUSrc = 0, MemtoReg = 0, MemWrite = 0, MemRead = 0, Branch = 1） -> 从 RegFile 读取 rs1, rs2 -> ALU 计算 -> ALU 计算结果控制二路选择器 -> 选择器选择 PC + 4 或者 PC + offset

课后习题

没习题，单周期 CPU：https://github.com/Su1furicAcid/SingleCycleCPU

多周期 CPU

知识回顾

实际上，单周期 CPU 的时钟频率受限于最慢的那一步，比如访存，这会让 CPU 浪费很多时间；而且，我们在上面把 CPU 划分成了很多单元，在某个单元工作时，其他单元竟然是空闲的，这也造成了一定的浪费

我们将 CPU 划分为五个阶段：取指（IF），译码（ID），执行（EX），访存（MEM），写回（WB）

流水线冒险：

流水线提高了效率，同时也引入了一些问题，比如结构冒险（硬件资源出现竞争）、数据冒险（某条指令依赖于之前还未完成的指令）、控制冒险（分支指令依赖于之前的指令）

1. R 型指令引起的数据冒险

对于下面这种情况：

add x19, x0, x1
sub x2, x19, x3 

这是一种用 nop 指令解决数据冒险的方法；然而可以发现，下一个 R 型指令依赖的数据在上一个 R 型指令的 EXE 阶段就已经计算出来了，没有必要等到 WB 阶段才写回，可以加入一个旁路，把计算结果直接传递给下一个指令

称为前递或者旁路

对于更复杂的情况：

sub x2, x1, x3
and x12, x2, x5
or x13, x6, x2

第一条指令分别和第二条指令、第三条指令都发生了数据冒险！而且不同于上面的例子，第一条指令和第三条指令发生的冒险，需要一个从 MEM 后出发的旁路（而不是 EXE）；在后面的实现过程中我们会讨论这个问题

2. Load 引起的数据冒险

对于下面这种情况：

lw x19, 0(x1)
add x2, x19, x3

同样的，我们依赖的数据在 Mem 阶段就已经得到了，可以直接传递给下一个指令

与 R 型指令引起的数据冒险不同，Load 引起的数据冒险需要在 MEM 阶段解决

在具体流水线的实现中，这样的分类方式会带来好处

通过编译器优化，可以减少数据冒险的发生

3. 控制冒险

对于下面这个例子：

add x19, x0, x1
beq x19, x0, 0x100

在绝大多数情况下，我们不可能在 ID 阶段就计算出分支的结果；为了避免无效的等待，可以预测分支的结果，在静态预测下，我们认为分支总是发生 / 不发生；在动态预测下，我们可以通过历史记录来预测分支的结果

在具体讨论如何利用历史记录预测前，先介绍流水线化的数据通路：

大部分的数据都是从左往右流动的，但是 PC 和 RegFile 的写入是逆向流动的；这两种逆向流动分别导致了控制冒险和数据冒险，想象一条流动的河流，下游有一个投石器向上游投掷颜料，那么颜料将会污染先前流动的水（这其实是个科幻小说的例子来着 😃 ）

数据通路的表示：多周期流水线图、单周期流水线图

之前在设计单周期 CPU 时提到了组合逻辑单元——当输入变化时，输出立即发生变化。这会引起一个问题，后面进来的指令会把前面的指令冲刷掉：假设 EXE 阶段需要 200 个时钟周期，而 MEM 阶段需要 300 个时钟周期，那么 MEM 的数据必然会受到 EXE 的影响

引入流水线寄存器，用于暂存上一个阶段的数据，这样就可以解决这个问题

然而这图有问题，RegFile 的写入是在 WB 阶段，然而这个线却从 IF / ID 连出来，写入的地址和数据来自于下一条指令

从单周期流水线图判断当前周期：

关于数据通路还有两个问题没有解决：1. 流水线下的控制信号 2. 前递或旁路

类似于单周期 CPU，在 ID 阶段产生控制信号；将控制信号分为三组（EXE：ALUOp，ALUSrc；MEM：MemWrite，MemRead，Branch；WB：MemtoReg，RegWrite）

现在考虑前递，这块怪复杂的；在考虑前递时要结合流水线寄存器（数据存在了哪里？数据又要去往哪个流水线寄存器？）

考虑两种类型的数据冒险，第一种发生在上一条指令的 EXE 之后和当前指令的 EXE 之前；第二种发生在上一条指令的 MEM 之后和当前指令的 EXE 之前；分别对应着图中 sub - and 和 sub - or 两对指令

判断条件：

EX/MEM.RegisterRd = ID/EX.RegisterRs1 // 1a
EX/MEM.RegisterRd = ID/EX.RegisterRs2 // 1b
MEM/WB.RegisterRd = ID/EX.RegisterRs1 // 2a
MEM/WB.RegisterRd = ID/EX.RegisterRs2 // 2b

我初看的时候有个疑问：为什么使用这个阶段的流水线寄存器呢？整体前移一个阶段不是也可以吗？当然可以，判断受限于前递的实现方式，看下面就明白了。

当 RegWrite = 0 或者要写入 0 号寄存器时，前递也不应该发生，在判断时应当加上这两个条件；为什么不依靠 RegFile 的鲁棒性解决（如果 RegFile 写的很好，能够独立的解决这种情况）？同样，看下面的实现就明白了，观察旁路在什么时候发生作用？

太美了 😭

回到这个例子：

sub x2, x1, x3
and x12, x2, x5
or x13, x6, x2

同时出现了两个数据冒险，显然应该使用最近的数据来前递，那么 MEM 类型的前递仅仅在 EXE 类型的前递不发生时才发生

对于 load 引起的数据冒险，需要额外多等待一个周期，这个怎么实现捏

判断条件很简单：

ID/EX.MemRead = 1 and (ID/EX.RegisterRd = IF/ID.RegisterRs1 or ID/EX.RegisterRd = IF/ID.RegisterRs2)

一样的还要附加：

ID/EX.RegisterRd != 0 and ID/EX.RegWrite = 1

为啥这次判断这么早？因为我们要塞入 nop 指令

nop 的实现分如下几步：

1. IF/ID 寄存器的值不能改变

2. ID/EX 的所有控制信号写0

3. PC 不能进行 PC + 4 或者其他改变

当塞入 nop 指令后，后面的处理与 R 型指令的 MEM 类型前递相同

相比于全部覆写 0，还是增加一个选择器更有性价比，这也体现了流水线的妙处

对于控制冒险，首先考虑实现静态分支预测：

假如预测有问题，那么我们需要把被错误执行的指令清空：假设所有的分支指令都在 MEM 阶段得到值，那么就要清空 IF/ID 和 ID/EX 两个寄存器；但是要明确一个很简单的问题，不会出现没有清空完全的情况，毕竟得到值的时候，分支指令还在流水线里（我怎么会有这个疑问）

但是这样仍然造成了两次停顿，太慢了。一方面我们考虑动态分支预测，另一方面我们考虑把得到分支指令的值的阶段提前到 ID 阶段。分支地址计算很容易提前，额外添加一个加法器即可，复杂的是判断分支条件：

1. 新的前递逻辑

2. 万一有数据冒险呢

这部分是太复杂了吗，怎么书上没细说（

采用分支预测缓存或者历史分支表（BHT）来预测分支结果：

1 位预测机制：如果预测不正确，那么就改变预测结果（对预测位取反），否则保持不变

2 位预测机制：定义两位有限状态机，00表示强不跳转，01表示弱不跳转；10表示弱跳转，11表示强跳转

2 位预测机制仅仅使用特定分支的信息，同时使用局部分支和最近执行分支的全局行为的信息可以得到更高的预测准确率，也即相关预测器；另一种分支预测方法是使用锦标赛预测器，对于每个分支使用多种预测器，并最终给出最佳的预测结果。

流水线的部分接近结束，最后两个话题是异常（或者叫例外）和中断；在很多情况下经常不区分异常和中断，在这里我们认为异常指处理器内部的意外的控制流变化，中断指处理器外部事件引起的控制流变化

当异常发生时，在系统异常程序计数器（SEPC）中保存发生异常的指令地址，同时将控制权转交给操作系统；RISC-V 设置系统例外原因寄存器（SCAUSE）来保存异常原因，还有一些机器比如 x86 则采用向量中断的方式，用基址寄存器加上编码后的例外原因（作为偏移）作为目标地址完成控制流转换

前面说过，已经将分支指令提前到 ID 阶段，那么当发生异常时，我们需要把异常指令的地址保存到 SPEC 中，同时把 PC 的值设置为异常处理程序的地址；还需要 IF.Flush 和 EXE.Flush 两个控制信号，用于清空流水线

RISC-V 中使用 0000 0000 1C09 0000 作为异常处理程序的地址

SEPC 寄存器保存引发异常的指令的地址，SCAUSE 保存最高优先级的异常原因

课后习题

作业除了有点麻烦还怪糖的 🤔

这道题没办法解释啊...姑且认为是计算关键路径上的元件就好...这题什么玩意...

写了几个答案，妈的说服不了自己，不贴了

1. 对于需要将内存写回寄存器的指令会执行错误：load

2. 对于需要做立即数加法的指令会执行错误：I 型指令，store；jalr 算不算要看具体实现，我给出的单周期 CPU 实现中，对于 jalr 定义了一个加法器，所以不会错，如果从 ALU 做计算，那么会有问题

大而快！层次化存储

知识回顾

特码的写不动了，我上课学了这么多东西？

时间局部性：如果一个数据被访问，那么在不久的将来它可能再次被访问

空间局部性：如果一个数据被访问，那么在不久的将来它附近的数据也可能被访问

这两个局部性是存储器层次化的基础

CPU -> Cache(SRAM) -> Memory(DRAM) -> Disk

SRAM（静态随机存取存储器）

具体工作原理

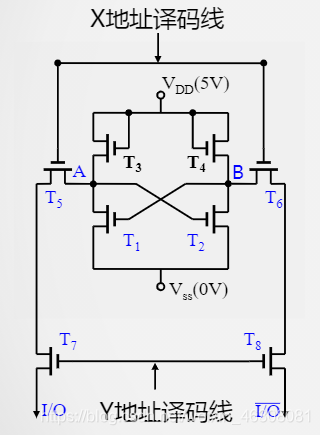
“随机”：从任何位置读取数据的时间代价都是一样的

“静态”：相对于DRAM，数据在 SRAM 中不需要刷新

因为 VDD 的存在，SRAM 属于易失性存储器

DRAM（动态随机存取存储器）

具体工作原理

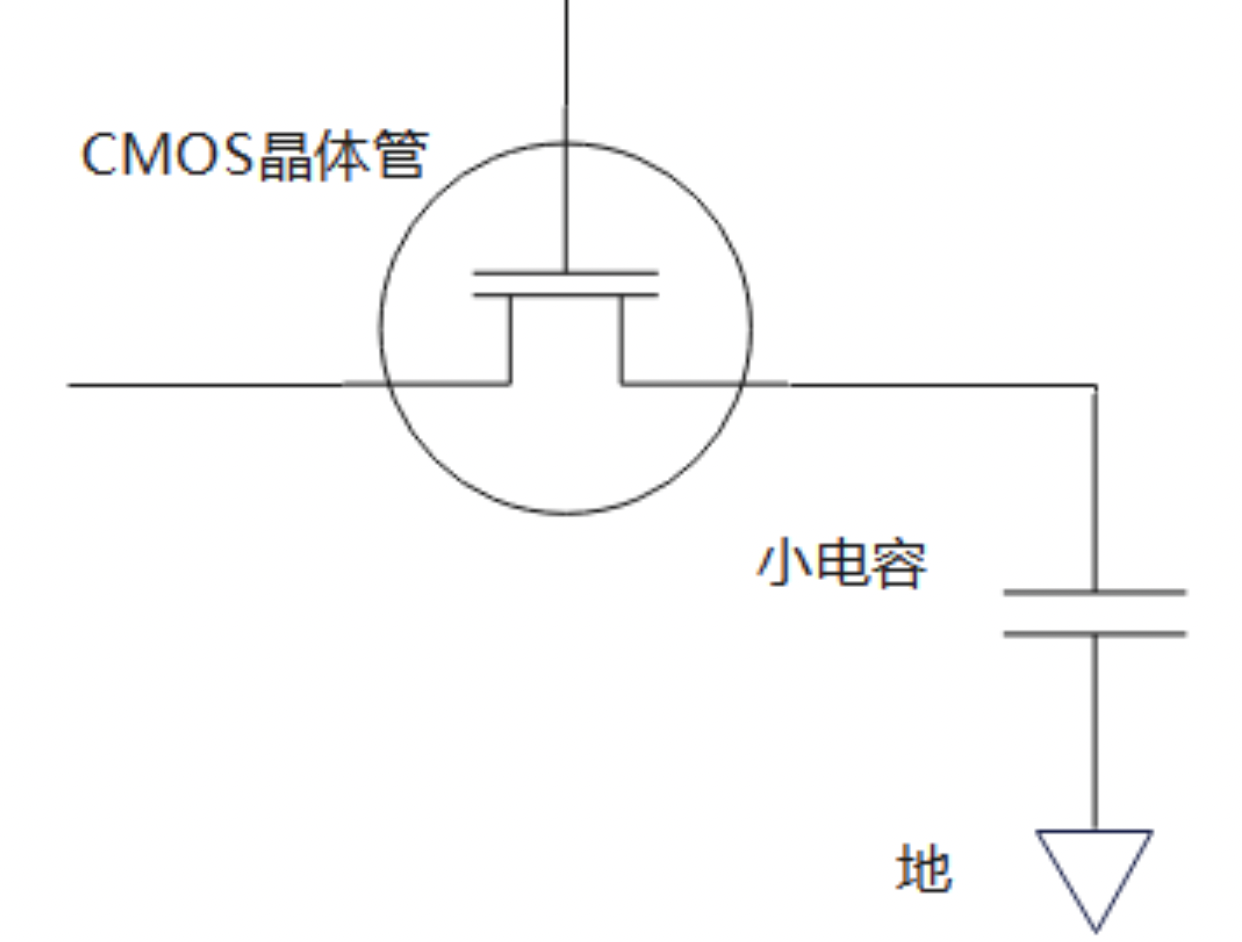
因为 DRAM 使用单个电容接地来存储，面临两个问题：1. 电容的电荷会泄漏，需要周期性刷新 2. 读取数据时，电容的电荷会被读取，“流出来”，需要读出后反写回去

“随机”：从任何位置读取数据的时间代价都是一样的

“动态”：相对于 SRAM，数据在 DRAM 中需要刷新和反写

显然 DRAM 属于易失性存储器，不上电刷新全消失给你看

现代 DRAM 以体（bank）的方式来组织结构

为更好地优化与处理器的接口，DRAM 添加了时钟，被称为同步 DRAM；双倍数据传输率意味着在时钟的上升沿和下降沿都可以进行数据传输；在 DRAM 的内部结构，允许同时对多个体发送一个地址来同时读和写这些 bank，称为交叉地址访问

Flash

分为 NOR 和 NAND 两种；NOR 常用在嵌入式系统中的指令存储器；NAND 常用在 USB 设备

Flash 的写操作会对器件本身产生磨损，大多数的 Flash 都支持耗损均衡（wear leveling）来将发生多次写的块的数据映射到较少被写的块

磁盘

每个磁盘通常包含多个盘片；每个盘片表面被分为若干同心圆，称为磁道；每条刺刀按顺序被划分为上千个扇区，扇区的容量一般为 512 ~ 4096 字节；一个扇区如下所示：

|GAP 1|ID|GAP 2|DATA|ECC|GAP 3|...

GAP 为间隙，ID 为扇区 ID，DATA 为数据，ECC 为纠错码；在 ID 和 DATA 中使用了循环冗余校验（CRC）技术

每个盘面都分配有一个磁头，各个盘面的磁头平行连接在一起，因此磁头的移动可以同时读写每个盘面的每一条磁道

操作系统通过三步完成对磁盘的数据访问：

1. 寻道：将磁头定位到正确的磁道上方，耗费的时间称为寻道时间

2. 旋转：等待所需的扇区旋转到磁头下方，耗费的时间称为旋转时间

3. 传输：将数据从磁盘传输到内存，耗费的时间称为传输时间

硬件结束了，终于来到抽象的 Cache 和 Memory 的世界 😂

Cache 是 Memory 部分内容的映像，与 Memory 之间以块为单位进行交换；那么想要建立一个 Cache，面临两个问题：1. 如何确定数据在 Cache 中的位置 2. 如何确定 Cache 中的数据是我需要的数据呢

为了解决这俩问题，我们引入了 Cache 的映射方式（类似于 Hash），有三种映射方式：直接映射、全相联映射、组相联映射：

假设我们建立的 Cache 有 n 个块，每个块是 1 个字（4 个字节）

1. 直接映射：取模运算天然的把自然数集合划分为 n 个互不相交的子集；同样地，我们把内存地址对 n 取模的结果作为 Cache 的索引；这样会带来新的问题，n+1 和 2n+1 会映射到同一个位置，这种现象称为冲突，我们把内存地址对 n 整除的结果称为标记；这种方式的一个天然优势是其天然的符合二进制的移位运算

\[\text{Cache Index} = \text{Memory Addr} \mod n \]

但是，无效数据不仅仅来自于冲突，还有可能来自于 Cache 启动时的随机数据，为了避免这种情况，我们引入了有效位（valid bit）；当 Cache 中的数据有效时，valid bit 为 1，否则为 0；当进行一次有效的写入时，valid bit 会被置为 1

一次失效并写入 Cache 的过程：

注意到题目中使用 Word Addr 而非 Memory Addr，因为每个 Cache 块的大小我们认为是 4 个字节（1 个字），所以我们需要将 Byte Addr 右移 2 位来得到 Word Addr，用 Memory Addr 就太宽泛了（没有指定大小）

2. 全相联映射：在直接映射中，假如真的有个需求要访问 n+1，2n+1，3n+1 ... 一方面，冲突太多，Cache 再快，写入也是需要时间的；另一方面，大量的 Cache 被浪费了。为了根治这个问题，我们可以设计这样一个 Cache：Memory 中的某个数据块可能与任意一个 Cache 块相连（或者说是映射到），这样的 Cache 称为全相联映射

这样做的话，Tag 位的长度就会加长，以整个子地址作为 Tag，每次访问时要对每一个 Cache 块进行比较，这也带来了时间开销

还有一个问题，如果 Cache 塞满了，我又要添加一个新的数据进入 Cache，我该替换谁？一种策略是先进先出（FIFO），最常用的另一种策略是最近最少使用（LRU），即替换最近最少被访问的 Cache 块

3. 组相联映射：组相联是介于直接映射和全相联映射之间的一种平衡；Cache 被划分为若干个组，每个组中包含若干 Cache 块；组中的 Cache 块与 Memory 数据块是全相联的，Memory 数据块又以直接映射的方式映射到每个组中

\[\text{Cache Index} = \text{Memory Addr} \mod \text{Number of Groups} \]

m 路组相联映射：每个组中有 m 个 Cache 块，此时，组内 Tag 等于 Memory Addr 整除组数的结果；直接映射和全相联映射都可以看作组相联的特例

对于 Cache 的写入，如果 Cache 命中有两种策略：写回（write back）和写直达（write through）；写回策略是指新值写入 Cache 中，只有在 Cache 块被替换时才写回到 Memory，写直达策略是指每次写入 Cache 时也写入 Memory

为了在替换 Cache 块时区分 Cache 块有没有被改写，引入脏位（Dirty）记录块是否被修改

如果 Cache 没命中，分为写分配（write allocate）和非写分配（write no-allocate）；写分配是指将数据块从 Memory 读入 Cache 后再写入 Cache（也就是写返回），非写分配是指直接写入 Memory

Cache 的性能评估：

\[\text{等待存储访问的时钟周期数} = \frac{访存操作数目}{程序指令数目} \times \frac{失效次数}{访存操作数目} \times \text{写失效代价} \]

\[\text{实际CPI} = \text{基准CPI} + \text{等待存储访问的时钟周期数} \]

直接看不太好理解，下面的例题不错：

\[\text{平均存储访问时间(AMAT)} = \text{命中时间} + \text{失效率} \times \text{失效代价} \]

\[\text{可用性} = \frac{\text{平均修复时间MTTF}}{\text{平均修复时间MTTF} + \text{平均失效间隔时间MTTR}} \]

现代 Cache 大多支持多级 Cache，此时有：

\[\text{全局缺失率} = \text{L1缺失率} \times \text{L2缺失率} \]

在 Cache 的基础上，考虑矩阵乘法如何在 CPU 上优化

// 矩阵乘法
for (int i = 0; i < n; i++) {
    // 主要研究下面这个循环
    for (int j = 0; j < n; j++) {
        for (int k = 0; k < n; k++) {
            C[i][j] += A[i][k] * B[k][j];
        }
    }
}

如果 Cache 恰好可以保存 3 个 \(n*n\) 的矩阵，那实际上不会发生任何失效；如果更小，不可避免的会发生多次失效，下面具体分析一下这个过程：

假设 Cache 块的大小为 4 Byte，一共有 8 个 Cache 块，全相联，矩阵为 8 * 8的 int 类型，忽略 Cache 对 C 造成的影响

计算 C[0][0] 时：

访问 A[0][0] 和 B[0][0]，均未命中，把 A[0][0 ~ 3] 和 B[0][0 ~ 3] 放进了 Cache

访问 A[0][1] 和 B[1][0]，A[0][1] 命中，B[1][0] 未命中，把 B[1][0 ~ 3] 放进了 Cache

访问 A[0][2] 和 B[2][0]，A[0][2] 命中，B[2][0] 未命中，把 B[2][0 ~ 3] 放进了 Cache

访问 A[0][3] 和 B[3][0]，A[0][3] 命中，B[3][0] 未命中，把 B[3][0 ~ 3] 放进了 Cache

访问 A[0][4] 和 B[4][0]，A[0][4] 未命中，B[4][0] 未命中，把 A[0][4 ~ 7] 和 B[4][0 ~ 3] 放进了 Cache

访问 A[0][5] 和 B[5][0]，A[0][5] 命中，B[5][0] 未命中，把 B[5][0 ~ 3] 放进了 Cache

访问 A[0][6] 和 B[6][0]，A[0][6] 命中，B[6][0] 未命中，用 B[6][0 ~ 3] 替换了 B[0][0 ~ 3]

访问 A[0][7] 和 B[7][0]，A[0][7] 命中，B[7][0] 未命中，用 B[7][0 ~ 3] 替换了 B[1][0 ~ 3]

A 发生了 2 次失效，B 发生了 8 次失效，总共 10 次失效

然后计算 C[0][1]，上面的故事重演

容易发现，失效来源于 A 的相邻 Cache 块没有被提前放进来，可以称其为空间局部性失效；还来源于B 的历史 Cache 信息并没有被充分利用（而被轻易替换掉了），可以称其为时间局部性失效

如下的分块矩阵乘法可以减少失效：

void do_block(int n, int si, int sj, int sk, int **A, int **B, int **C) {
    for (int i = si; i < si + BLOCK_SIZE; i++) {
        for (int j = sj; j < sj + BLOCK_SIZE; j++) {
            for (int k = sk; k < sk + BLOCK_SIZE; k++) {
                C[i][j] += A[i][k] * B[k][j];
            }
        }
    }
}

void dgimm(int n, int **A, int **B, int **C) {
    for (int si = 0; si < n; si += BLOCK_SIZE) {
        for (int sj = 0; sj < n; sj += BLOCK_SIZE) {
            for (int sk = 0; sk < n; sk += BLOCK_SIZE) {
                do_block(n, si, sj, sk, A, B, C);
            }
        }
    }
}

易证分块算法的正确性，接下来分析其为什么优化了 Cache 的性能

对于上面那个例子，当计算到 A[0][3] * B[3][0] 时，接下来不再继续计算 A[0][4] * B[4][0]，而转向去计算 A[1][0] * B[0][1]，充分利用了 B 的历史 Cache 信息

参考

奇偶校验：在奇校验中，如果数据单元中1的数量已经是奇数，则校验位设置为0；否则，校验位设置为1。同理，在偶校验中，如果数据单元中1的数量已经是偶数，则校验位设置为0；否则，校验位设置为1。

汉明编码：

奇偶校验码不能纠正错误，也无法检测到偶数个错误；汉明校验使用更多的校验码来确定单个错误的位置：

1. 从左到右从 1 开始编号

2. 将编号为 2 的幂次方的位作为奇偶校验位

3. 剩余其他位作为数据位

4. 校验位 1（0001）检查编号最后一位同样为 1 的数据位，进行偶校验；校验位 2 （0010）检查编号倒数第二位同样为 1 的数据位，进行偶校验；以此类推

前面讨论了 Memory <-> Cache，现在讨论 Disk <-> Memory 的数据传输

现代操作系统为进程创建一个虚拟内存空间，这一技术允许在多个进程之间高效安全的共享内存，加强了对各个程序地址空间额隔离，同时也允许程序使用比物理内存更大的内存空间（虚拟内存会自动地管理物理内存和磁盘之间的数据传输）

本书中的 Cache 对应着物理地址空间

虚拟存储很类似于 Cache，但是使用的术语不同。虚拟存储块称为页，虚拟存储失效称为缺页失效，虚拟地址向真实地址的转换称为地址转换。

这里的 RISC-V 使用三十二位地址，图中假设物理内存为 1GiB，需要 30 位地址，页大小为 4KiB，需要 12 位地址，相应的，物理页号为 18 位，虚拟页号为 20 位

• 这里的页是全相联

• 最近最少使用（LRU）算法

• 采用写回法而非写直达法（写穿透），因此需要一个额外的脏位

我们使用页表来实现地址转换。页表使用虚拟地址中的页号作为索引，找到相应的物理页号（值得注意的是，页表本身并不储存虚拟页号）；有效位的定义与 Cache 类似。与前文的思想相同，每个进程都有一张独立的页表。

完全准确地执行 LRU 的成本是巨大的，为了帮助操作系统估算最近最少使用的页，RISC-V 提供了一个引用位（或者叫使用位），当该页被访问时这个位被用来记录，操作系统定期将引用位清零

反向页表：参考

多级页表：参考

由于页表存储在主存中，因此程序每个访存请求至少需要两次访存，第一次访存获得物理地址，第二次访存获得数据。访存同样具备局部性，因此，现代处理器通常包含一个特殊的 Cache 追踪最近使用过的页表项，称为 TLB（Translation Lookaside Buffer）

这张图展示了 TLB 命中后如何在 Cache 中或者 Memory 中找到数据的过程

想要更深入理解，得看习题：

课后习题

5.2.1

访存地址以字地址的形式给出，每个Cache块为1个字，所以给出的地址在数值上等于主存块号

在直接映射下：

访存地址	二进制地址	Cache 块号	Tag	是否命中
0x03	0000 0011	3	0	失效
0xb4	1011 0100	4	11	失效
0x2b	0010 1011	11	2	失效
0x02	0000 0010	2	0	失效
0xbf	1011 1111	15	11	失效
0x58	0101 1000	8	5	失效
0xbe	1011 1110	14	11	失效
0x0e	0000 1110	14	0	失效
0xb5	1011 0101	5	11	失效
0x2c	0010 1100	12	2	失效
0xba	1011 1010	10	11	失效
0xfd	1111 1101	13	15	失效

5.2.2

在直接映射下：

访存地址	二进制地址	主存块号	Cache 块号	Tag	是否命中
0x03	0000 0011	1	1	0	失效
0xb4	1011 0100	90	2	11	失效
0x2b	0010 1011	21	5	2	失效
0x02	0000 0010	1	1	0	命中
0xbf	1011 1111	95	7	11	失效
0x58	0101 1000	44	4	5	失效
0xbe	1011 1110	95	7	11	命中
0x0e	0000 1110	7	7	0	失效
0xb5	1011 0101	90	2	11	命中
0x2c	0010 1100	22	6	2	失效
0xba	1011 1010	93	5	11	失效
0xfd	1111 1101	126	6	15	失效

5.2.3

在直接映射下：

对于C1，8个Cache块，每个Cache块为1个字

访存地址	二进制地址	Cache 块号	Tag	是否命中
0x03	0000 0011	3	0	失效
0xb4	1011 0100	4	22	失效
0x2b	0010 1011	3	3	失效
0x02	0000 0010	2	0	失效
0xbf	1011 1111	7	23	失效
0x58	0101 1000	0	11	失效
0xbe	1011 1110	6	23	失效
0x0e	0000 1110	6	0	失效
0xb5	1011 0101	5	22	失效
0x2c	0010 1100	4	3	失效
0xba	1011 1010	5	23	失效
0xfd	1111 1101	7	31	失效

对于C2，4个Cache块，每个Cache块为2个字

访存地址	二进制地址	主存块号	Cache 块号	Tag	是否命中
0x03	0000 0011	1	1	0	失效
0xb4	1011 0100	90	2	22	失效
0x2b	0010 1011	21	1	3	失效
0x02	0000 0010	1	1	0	失效
0xbf	1011 1111	95	3	23	失效
0x58	0101 1000	44	0	11	失效
0xbe	1011 1110	95	3	23	命中
0x0e	0000 1110	7	3	0	失效
0xb5	1011 0101	90	2	22	命中
0x2c	0010 1100	22	2	3	失效
0xba	1011 1010	93	1	23	失效
0xfd	1111 1101	126	2	15	失效

对于C3，2个Cache块，每个Cache块为4个字

访存地址	二进制地址	主存块号	Cache 块号	Tag	是否命中
0x03	0000 0011	0	0	0	失效
0xb4	1011 0100	45	1	22	失效
0x2b	0010 1011	10	0	3	失效
0x02	0000 0010	0	0	0	失效
0xbf	1011 1111	47	1	23	失效
0x58	0101 1000	22	0	11	失效
0xbe	1011 1110	47	1	23	命中
0x0e	0000 1110	3	0	0	失效
0xb5	1011 0101	45	1	22	失效
0x2c	0010 1100	11	0	3	失效
0xba	1011 1010	46	1	23	失效
0xfd	1111 1101	63	1	31	失效

使用方案C2，C2 的命中率最高，缺失率最低

做这道题的时候注意字地址和 Cache 块的大小之间的联系

5.3.1

Cache 总大小 32KiB

\[32 \times 2^{10} = 2^5 \times 2^{10} = 2^{15} \text{ Byte} \]

块大小为 2 个字

\[2 \times 4 = 2^4 \text{ Byte} \]

Cache 块数

\[\frac{2^{15}}{2^4} = 2^{11} \text{ 块} \]

对于 64 位字节地址，Tag 的长度

\[64 - 11 - 4 = 49 \text{ 位} \]

添加 1 位有效位，所以总共 50 位

这 50 位是为了满足正确 32KiB 存储所付出的索引代价，计算总位数

\(2^{15} * 8 + 2^{11} * 50 = 364544 \text{ 位}\)

5.3.2

计算方法类似

5.10.1

\(f_1 = \frac{1}{0.66ns} = 1.515GHz\)

\(f_2 = \frac{1}{0.90ns} = 1.111GHz\)

5.10.2

\[\text{平均存储访问时间(AMAT)} = \text{命中时间} + \text{失效率} \times \text{失效代价} \]

\(AMAT_1 = \frac{0.66ns + 0.08 * 70ns}{0.66} = 9.48 cycles\)

\(AMAT_2 = \frac{0.90ns + 0.06 * 70ns}{0.90} = 5.67 cycles\)

5.10.3

\[\text{等待存储访问的时钟周期数} = \frac{访存操作数目}{程序指令数目} \times \frac{失效次数}{访存操作数目} \times \text{写失效代价} \]

\[\text{实际CPI} = \text{基准CPI} + \text{等待存储访问的时钟周期数} \]

\(CPI_1 = 1 + 1 * 0.08 * \frac{70}{0.66} + 0.36 * 0.08 * \frac{70}{0.66} = 12.54\)

\(CPI_2 = 1 + 1 * 0.06 * \frac{70}{0.90} + 0.36 * 0.06 * \frac{70}{0.90} = 7.35\)

注意不要忽略了指令存储器的访问

5.10.4

\(AMAT_1 = \frac{0.66ns + 0.08 * (5.62 + 0.95 * 70ns)}{0.66} = 9.74 cycles\)

5.10.5

\(CPI_1 = 1 + 1 * 0.08 * \frac{5.62 + 0.95 * 70}{0.66} + 0.36 * 0.08 * \frac{5.62 + 0.95 * 70}{0.66} = 13.40\)

5.18.1

页大小指实际物理内存分页时页的大小，也就是说，当页大小为 4KiB 时，page offset 为 12 位

虚拟地址空间大小为 43 位，因此页表项数目为 \(2^{43 - 12} = 2^{31}\)

页表需要物理内存为 \(2^{31} * 4 = 2^{33}\) 字节

5.18.4

\(\frac{4 KiB}{4 B} = 2^{10}\)

实际上就是计算一个树的深度，这棵树的叶子节点有 \(2^{31}\) 个，每个非叶子节点可以有 \(2^{10}\) 个子节点

容易得出需要 4 层

期末试题解析

放一点具有复习价值的题目

21-22 hy期末试卷A

Q1.

指令 beq 所在的地址为 0x0000 0000 0008 0024，转移目标地址为 0x0000 0000 0008 0010，则此指令中立即数的十六进制表示为

首先做一个十六进制减法，得到立即数的十进制表示为 -(16 + 4) = -20

其次，这个题目考察的是指令中的立即数，通过 SB 指令格式可知，立即数是 -20 / 2 = -10

所以答案是 0xFFFFFFF6

实际上，编译器更倾向于使用 beq label 的形式，而不是 beq $rs, $rt, offset 的形式

Q2.

考虑一个循环，在程序中会被调用多次。每次执行时，循环结束时的分支指令会发生 9 次跳转到循环开始，之后产生 1 次不跳转。采用 1 位预测机制和采用 2 位预测机制的准确率分别是

这个题一开始我觉得有些奇怪，他没有给出初始状态

后来明白实际上要求的是期望值，而非一次执行的结果

对于 1 位预测机制，假设初始状态为不跳转，那么显然会有 8 次正确预测，2 次错误预测，准确率为 80%

对于 2 位预测机制，假设初始状态为弱跳转，那么显然会有 9 次正确预测，1 次错误预测，准确率为 90%

之所以这么设置，是因为这样可以保证每次执行时进入这个状态机和离开这个状态机的状态是一样的，可以保证每次执行的动作相同，得出的自然就是期望值

Q3.

假定一个磁盘的转速为 7200RPM，磁盘的平均寻道时间为 8ms，内部数据传输率为 4MB/s，不考虑排队等待时间，则读一个 512B 扇区的平均时间大约为

7200 RPM -> 7200 rounds per minute -> 120 rounds per second

总时间 = 等待旋转的期望时间（1/2 圈）+ 寻道时间 + 传输时间

算出来约为 12.29 ms

Q4.

假定主存地址为 32 位，按字节编址，主存和 Cache 之间采用直接映射方式，主存块大小为 4 个字，每字 32 位，采用回写(write back)方式，则能存放 4K 字数据的 Cache 的总容量的位数至少是

Cache 能存放 4K 字数据（数据容量为 4K），块大小为 4 个字，所以 Cache 块数为 1K = 2^10，Cache 块号需要 10 位

主存地址为 32 位字节地址，主存块大小为 4 个字也即 2^4=16 字节，所以块内偏移占 4 位

Tag 需要 32 - 10 - 4 = 18 位

需要 1 位有效位

写回法需要一个 1 位的脏位

所以 Cache 需要的总容量的位数为 (Tag + Valid + Dirty) * Cache 块数 + 4K * 4 * 8 = (20 + 16 * 8) * 2^10 = 148K

（这里不区分 K 和 Ki）

Q5.

假设有一个虚构的 8 位浮点数标准，称为“minifloat”（如：S E EEMMMM，其中符号字段 1 位，指数字段 3 位，尾数字段 4 位），其它属性和 IEEE754 标准一样（如：偏阶，非规格化数值，∞， NaNs，等等）。
（1）请问偏阶是多少？在[1, 4)范围内有多少个 minifloat？（4 分）
（2）请写出大于 1 的最小 minifloat 数，用十进制数表示。（3 分）
（3）用一条 RISC_V 整数运算指令实现 times2，假设 f（上面粗体显示）最左边的“E”位为 0。（3 分）

minifloat times2 ( minifloat f ) { return f * 2.0; }
times2: ______ a0, a0, ______ # 假设 f 存在寄存器 a0 最低字节
jalr x0， 0(x1)

（1）偏阶 = 2^(n-1) - 1 = 2^(3-1) - 1 = 3；

枚举 [1, 4) 范围内的 minifloat

E = 1, M = 0000 ~ 1111, 表示范围从 1 ~ 2 - 1/16

E = 2, M = 0000 ~ 1111, 表示范围从 2 ~ 4 - 1/16

一共 16 + 16 = 32 个

（2）大于 1 的最小 minifloat 数为 1.0001，对应的十进制数为 1 + 1/16 = 1.0625

（3）考虑把 E + 1 即可

minifloat times2 ( minifloat f ) { return f * 2.0; }
times2: addi, a0, a0, 0x10
jalr x0, 0(x1)

Q6.

在增加了阻塞单元的流水线上执行如下指令序列：

nop
nop
lw x10, 0(x10)
addi x10, x11, -4
add x12, x12, x10

从取第一条指令开始计时，请在下面的表格中填写各时钟周期阻塞单元的输入输出信号状态值：

画出多周期流水线图可以很快求解，就是有点麻烦，没啥思维难度

总体来说卷子还行，难度一般 😊

21-22 hy期末试卷B

？我犯天条了我做英文卷子啊

怎么考汉明编码，还得复习下

Q1.

Write the RISC_V assembly code that creates the 32-bit constant 0x20014924 and stores that value to register x19.

lui x19, 0x20014
ori x19, x19, 0x924

利用 lui 把一个 32 位常数赋值给寄存器

If the current value of the PC is 0x1FFFF000, can you use beq to get to the pc address as stored in register x19? You must clearly show your work to receive credit.

考虑 SB 型指令包含 12 位立即数（实际上是 13 位）

那么 SB 型指令能够跳转的范围有 0x1000 ~ 0x0FFE，无法跳转到 0x20014924

Q2.

RISC_V assembly code, Argument n in $x10, Result in $x1.

int power(int n) 
{ 
    if (n==0) { 
        return(1); 
    } else { 
        return(2*power(n-1)); 
    } 
}

Loop: 
    addi sp, sp, (1) 
    sd x1, (2)
    sd x10, 0(sp)
    bne (3), x0, (4) 
    addi x10, x0, (5) 
    addi sp, sp, (6) 
    jalr x0, (7) 
L1：
    addi x10, x10, (8) 
    jal x1, (9) 
    ld x10, 0(sp)
    ld x1, (10) 
    addi sp, sp, (11) 
    add x10, x10, (12) 
    jalr x0, (13) 

其实难度也还可以接受，注意 jalr 的格式

Loop: 
    addi sp, sp, -16 
    sd x1, 8(sp)
    sd x10, 0(sp)
    bne x10, x0, L1 
    addi x10, x0, 1 
    addi sp, sp, 16 
    jalr x0, 0(x1)
L1：
    addi x10, x10, -1 
    jal x1, Loop 
    ld x10, 0(sp)
    ld x1, 8(sp) 
    addi sp, sp, 16
    add x10, x10, x10 
    jalr x0, 0(x1) 

Q3.

考虑在上面的数据通路中添加一个新的指令 ss rs1, rs2, imm，功能是 Mem[rs1] = rs2 + imm，加入新的硬件单元

考虑在 ALU 中完成 rs2 + imm，这需要我们在二进制指令中交换 rs1 和 rs2 的位置

需要有一条线路从 ALU result 连接到 Data Memory 的 Write data，与原来的线路通过一个二路选择器，还需要一个线路从 Read data 2 连接到 Address，同样一个二路选择器

这题有点意思哈 😊

Q4.

Using Hamming Error Correction Code, how many check bits are needed for 64-bit data to find two errors and correct one error?

2^p >= 64 + p + 1

p = 7

又因为要能够检测两个错误，所以需要 p+1 = 8 位校验位

21-22 ai期末试卷A

Q1.

若有两种机器采用了不同方法来设计条件分支指令：
（a）P1：通过比较指令设置条件码，然后对条件码进行测试以决定分支。
（b）P2：分支指令中包含了比较操作。
在两种机器中，除了条件分支指令需要 2 个时钟周期之外，其他所有指令都只需 1 个时钟周期。原始的待执行指令中分支指令占 20%，对于 P1，需增加与分支指令数量相同的比较指令；而对于 P2，则不需要。已知 P2 的时钟周期是 P1 的 1.25 倍，那么：

（1）P1 的 CPI 是多少？（4 分）
（2）P2 的 CPI 是多少？（4 分）
（3）哪一个机器更快？（2 分）

这题标答是对的我直接吃

（1）P1 的 CPI = (8 * 1 + 2 * 2 + 2 * 1) / 12 = 7/6

（2）P2 的 CPI = (8 * 1 + 2 * 2) / 10 = 1.2

（3）CPU 运行时间 = 指令数 * CPI * 时钟周期；计算可得 P2 更快

Q2.

func:
    addi sp, sp, -16
    sd x1, 8(sp)
    sd x10, 0(sp)
    addi x5, x10, -1
    bge x5, x0, L1
    addi x10, x0, x0
    addi sp, sp, 16
    jalr x0, 0(x1)
L1:
    addi x10, x10, -1
    jal x1, func
    addi x6, x10, 0
    ld x10, 0(sp)
    ld x1, 8(sp)
    addi sp, sp, 16
    mul x7, x10, x10
    add x10, x6, x7
    jalr x0, 0(x1)

翻译成 C 代码

long long func(long long a) {
    if (a >= 1) {
        return a * a + func(a - 1);
    } else {
        return 0;
    }
}

Q3.

你正在设计处理器的 cache 系统，假设已经准备采用 write-allocate（写分配）
策略，块大小为 64B，所有的 load 和 store 都是针对 8 字节的位置进行的。总线支持 8B 和 64B 的事务处理，也就是从内存既能读写 8B 数据也能读写 64B 的数据。
（1）你不确定应该使用 write-back（写回）还是 write-through（直写）策略中的哪一种。于是你运行了一个 benchmark 程序，它每秒产生 10 亿次写操作而没有读操作，你的cache 的命中率为 X，那么在程序稳定时，两种写策略的写带宽（bytes/second）分别应该为多少？

出现了一个新概念——写带宽：写带宽是指写操作的数据量，单位是字节/秒

对于 write-back，考虑只有每次 Cache miss 并且发生替换的时候 Cache 块才会被写回 Memory，虽然只写 8 字节，但是每次写回一整块，所以为 64 字节，所以写带宽为 10^9 * (1 - X) * 64

对于 write-through，每次写操作都会写回 Memory，所以写带宽为 10^9 * min(8, 64) = 10^9 * 8

20-21 zg期末试卷A

Q1.

在一个没有旁路（前递/forwarding）和冒险检测的五阶段流水线中，寄存器在前
半个周期写，后半个周期读。如果想正确运行如下代码，至少需要插入几条 NOP 指令。

addi x11, x1, 5
ld x12, 0(x2)
add x13, x11, x12
addi x14, x12, 15
add x15, x13, x11

画多周期流水线图，可以看出需要插入 3 条 NOP 指令

Q2.

我合理怀疑今年考 load