一些NPC问题的证明
《算法设计与分析》期末复习
团集
把 SAT 在多项式时间内归约到团集
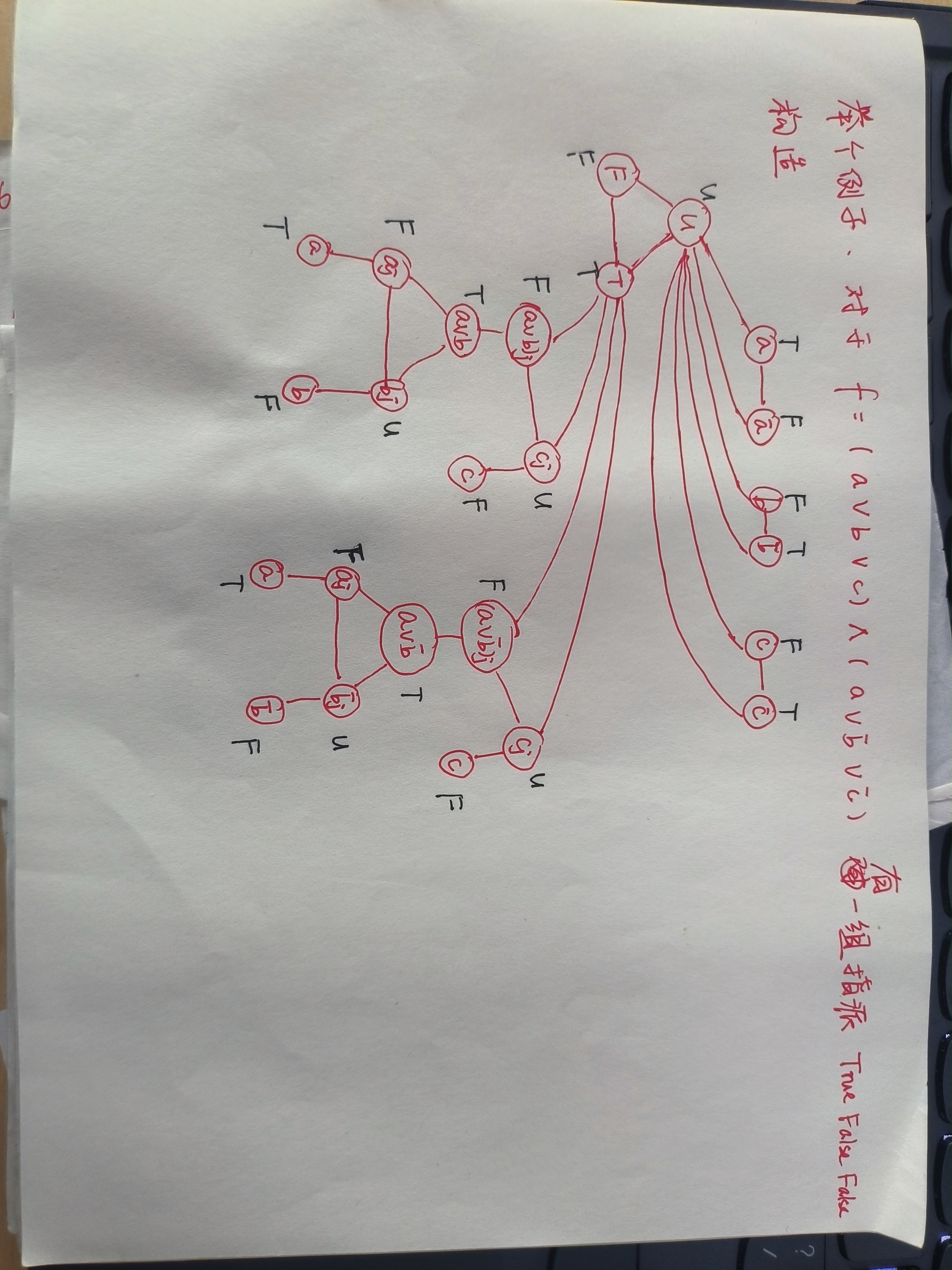
对于一个可满足性实例 $ f = C_1 \wedge C_2 \wedge ... \wedge C_m $
建立一张图 $ G (V, E) $
现在证明可满足性实例 \(f\) 是可满足的当且仅当 \(G(V,E)\) 有一个大小为 \(m\) 的团集
"=>"：可满足性实例 \(f\) 是可满足的，说明每个子句中最少都有一个文字为 1，认为文字为 1 在这张新建立的图中是被选中的，根据图的定义就得到了一个大小为 \(m\) 的团集
"<="：图中有一个大小为 \(m\) 的团集，假设有一个字句不为 1，那么至少有一个子句中有两个对应的文字被选中，根据定义这两个点没有边相连，所以假设错误
顶点覆盖
把 SAT 在多项式时间内归约到顶点覆盖
对于一个有 \(n\) 个文字 \(x_1, x_2, ..., x_n\) 的含有 \(m\) 个子句的可满足性实例 \(f = C_1 \wedge C_2 \wedge ... \wedge C_m\)
建立一张图 \(G(V,E)\)
-
对于任意 \(x_i\)，把\((x_i, \overline{x_i})\) 加入 \(E\) 中
-
对于一个子句 \(C_i\)，对于任意 \(x_i, x_j\)，均把它们相连加入 \(E\) 中，也就是构建一个大小为 \(|C_i|\) 的完全子图（上面说的团）
-
对于一个子句 \(C_i\)，把 \(C_i\) 内的任意文字 \(x_i\) 与 1. 中对应的点相连
-
令 $ k = n + \Sigma (|C_i| - 1) $
下面证明可满足性实例 \(f\) 是可满足的当且仅当 \(G(V,E)\) 有一个大小为 \(k\) 的顶点覆盖
"=>"：对于一个文字 \(x_i\)，如果其被指派为 1，那么在 \(G\) 中选择 \(x_i\)，否则选择 \(\overline{x_i}\)；因为每个子句中至少有一个文字为 1，对于每个子句组成的团，存在至少一个顶点 \(x_i\)，与之对应的文字被选中，那么 \((x_i, x_i)\) 这条边已经被覆盖了，再选择团（一个完全子图）内其他的所有点，一共 \(|C_i| - 1\) 个，所以我们找到了一个大小为 \(k\) 的顶点覆盖
"<="：\(G\) 有一个大小为 \(k\) 的顶点覆盖，首先考虑 1. 中构建的边必然要被覆盖，所以 \(x_i, \overline{x_i}\) 至少有一个被选中；又因为我们对每个子句构造了一个完全子图，它的顶点覆盖至少要 $ |C_i| - 1 $ 个点被选中；这样我们就保证的每个子句的结果必然为 1
独立集
考虑到顶点覆盖和独立集是完全相反的，完全可以把顶点覆盖在多项式时间内归约到独立集
图 \(G(V, E)\) 有顶点覆盖 \(S\) 当且仅当有独立集 $ V-S $
"=>"：图 \(G(V, E)\) 有一个顶点覆盖 \(S\)，对于图内的任意一条边 \((x_i, x_j)\)，\(x_i, x_j\) 至少有一个在 \(S\) 内，那么在 \(V-S\) 中，就不存在 \((x_i, x_j)\) 这条边
"<="：反之，对于图内任何一条边 \((x_i, x_j)\)，\(x_i, x_j\) 不可能同时出现在 \(V-S\) 中，那么至少有一个出现在 \(S\) 中
实际上，独立集也可以在多项式时间内归约到团集（图 \(G\) 的一个独立集是图 \(\overline{G}\) 的一个团集），又因为归约本身的传递性，顶点覆盖也可以归约到团集
3-SAT问题
显然是要把 SAT 在多项式时间内归约到 3-SAT
最麻烦的地方在于，SAT 中的某个子句可能含有任意字，且彼此之间是析取；我们要怎么转化成析取-（3项）合取形式的式子
对于一个子句 $ C_i $，有 $ C_i = x_1 \vee x_2 \vee ... \vee x_k $
当 $ k = 3 $，这是我们所希望的，不用做任何操作
当 $ k = 1 $，我们考虑加入两个额外变量，构造新的子句 $ C_i' = (x_1 \vee y_1 \vee y_2) \wedge (x_1 \vee \overline{y_1} \vee y_2) \wedge (x_1 \vee y_1 \vee \overline{y_2}) \wedge (x_1 \vee \overline{y_1} \wedge \overline{y_2}) $
当 \(x_1 = 0\)，令 \(y_1 = y_2 = 0\)；当 \(x_1 = 1\)，令 \(y_1 = y_2 = 1\)
当 $ k = 2 $，考虑加入一个额外变量，新的子句 $ C_i' = (x_1 \vee x_2 \vee y_1) \wedge (x_1 \vee x_2 \vee y_1) $
当 $ k >= 4 $，加入 $ k + 1 $ 个额外变量，新的子句
这个我还看到了很多构造方案，我觉得本质都差不多
既然在可满足性问题的一组解下，这个子句必然为 1，对于句内任何一个 \(x_i = 1\)，都可以很轻易构造出 \(y_1, ..., y_{k+1}\) 的一组解使得整个句子值为 1
所以完成了 SAT 到 3-SAT 的归约
3-Colorability 3着色问题
考虑将 3-SAT 归约到 3-Colorability
这个构造有点复杂 😦 但是很有意思 😃
很容易把 3-Colorability 归约到 k-Colorability
3 Dimensional Match 三维匹配问题
可以考虑把 3-Colorability 在多项式时间内归约到三维匹配问题
Hamilton Cycle / Path 哈密顿回路 / 路径问题
这群学数学的脑子怎么长的？
我倾向于构造的这张图对于 SAT / 3-SAT 归约到哈密顿回路都适用
哈密顿回路通过添加边权可以归约到旅行商问题
那么对于哈密顿路径，我们考虑将哈密顿回路在多项式时间内归约到哈密顿路径
上面的pdf已经给出了方案，将哈密顿路径中的某个点 \(v_i\) 拆成两个点 \(v_{i_1}\) 和 \(v_{i_2}\)，\(v_{i_1}\)只分配入度信息，\(v_{i_2}\) 只分配出度信息，两点之间不相连，这样就把一个路径断开了
Google 确实比 Bing 好用
Subset Sum 子集和问题
这个问题可以归约到 Set-Partition 划分问题和背包问题，所以提前列出来
不是哥们你考这个？
