9-Simple Typed Lambda Calculus

函数类型

因为纯粹的 lambda 演算是 turing 完备的，因此只有运行时才能够完全确定类型，比如：

if <complex evaluation> then true else (λx.x)

定义函数类型：λx.t: →；为了更加精确，加入参数 T1 T2，得到如下递归定义：

定义：类型 Bool 上的简单类型集合是由下列语法产生的：

T ::=
      Bool  (布尔类型)
      T → T  （函数类型）

类型构造子是右结合的，即 T1 → T2 → T3 ≡ T1 → (T2 → T3)，这也与直觉相吻合

类型关系

首先遇到的问题是：对于一个 abstraction，怎么知道参数是什么类型？

• 给参数添加类型注释（相当于给参数指派一个类型）；称为显式类型化 explicitly typed

• 分析抽象体，通过体中囿变量的行为逆推断参数类型；称为隐式类型化 implicitly typed

TaPL 集中讨论第一种方案

既然已知参数类型，那么函数结果的类型显然是抽象体的类型，表示为：

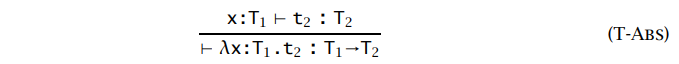
类型上下文 typing context

由于项 x 可能包含 lambda 抽象，所以为了保证推导的准确性，需要若干个同样的类型注释（也可以理解成一个指派 / 假设），因此我们拓展一下类型关系，添加一个类型上下文 typing context，记为 Γ；原先 t : T 的类型关系被扩展为 Γ ├ t : T 的一个三元关系；同时 comma 算子 , 被用来扩展 Γ，比如：Γ , x : T 意味着新的绑定 binding 被加入了这个上下文之中，Γ 可以看作从变量到类型的一个函数

为了防止新绑定和旧绑定之间的冲突，要求选择的变量名称不同于 Γ 中已经存在的变量名称

类型关系

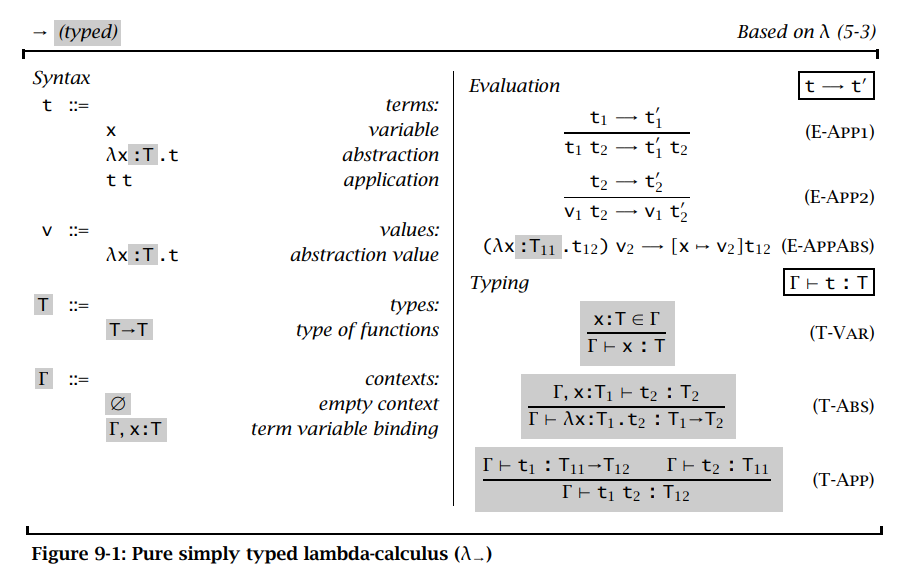
练习：不带基础类型的纯简单类型 lambda 演算实际是退化的，即没有良定项，为什么？

类型集合为空，归纳定义缺少 base

\(\lambda_\rightarrow\) 称为简单类型的 lambda 演算

简单类型的 lambda 演算的类型规则同样可以构建一棵推导树，比如说明 (λx : Bool .x) true 在 Γ 为空时类型为 Bool ：

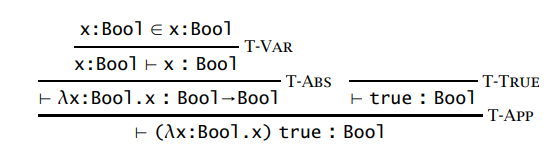
练习：证明 f : Bool → Bool ├ f (if false then true else false) : Bool

\(\frac{\frac{f:Bool \rightarrow Bool \in f:Bool \rightarrow Bool}{f:Bool \rightarrow Bool} \frac{if false then true else false}{false:Bool}}{f (if false then true else false):Bool}\)

练习：找一个上下文集合 Γ 使得在这个上下文中 f x y 有类型 Bool

可以描述成f : S → T → Bool, x : S, y : T

类型的性质 Properties

引理：（类型关系的逆）

定理：（类型唯一性）在一个给定的类型上下文 Γ 中，项 t 至多有一个类型

练习：是否存在某上下文 Γ 和类型 T 使得 Γ ├ x x : T？

假设存在，则根据逆引理(3)有 Γ ├ x : T' Γ ├ x : T' → T 进而有 T' → T = T' 这导致了无限长的递归形式的类型，而因为基础类型的存在使目前的简单类型系统的类型是有限长的，出现矛盾

引理：（典型形式）

利用典型形式引理可以证明进展定理

定理：（进展）假设 t 是封闭的 closed 良类型的项，则 t 要么是一个值，要么存在某个 t' 使得 t → t'

分不同情况讨论

引理：（置换）如果 Γ ├ t : T 并且 Δ 是 Γ 的一个替换 permutation，则 Δ ├ t : T

引理：（弱化）如果 Γ ├ t : T 并且 x ∉ dom(Γ) 则 Γ , x : S ├ t : T

引理：（代换引理）如果 Γ , x : S ├ t : T 并且 Γ ├ s : S，那么 Γ ├ [x → s]t : T

归纳证明：

• 情况 T-VAR：t = z with z : T ∈ (Γ , x : S)

如果 z = x，则 [x → s]t = s，为题设；如果 z ≠ x，则 [x → s]t = t，成立

• 情况 T-ABS：t = λy : T2 . t1 T = T2 → T1 Γ , x : S, y : T2 ├ t1 : T1

Γ , x : S, y : T2 ├ t1 : T1 利用弱化引理 Γ , y : T2 ├ t1 : T1

再由归纳假设 Γ , y : T2 ├ [x → s]t1 : T1 和 T-ABS 规则有：

Γ , x : S, λy : T2 . [x → s]t1 : T2 → T1

• 情况 T-APP：t = t1 t2 Γ , x : S ├ t1 : T2 → T1 Γ , x : S ├ t2 : T2

由归纳假设有 Γ , x : S ├ [x → s]t1 : T2 → T1 Γ , x : S ├ [x → s]t2 : T2

进而由 T-APP 有 Γ , x : S ├ [x → s]t1 [x → s]t2 : T1

• 情况 T-TRUE 和 T-FALSE：自然成立

• 情况 T-IF：t = if t1 then t2 else t2' Γ , x : S t1: T1 Γ , x : S t2: T2 Γ , x : S t2': T2

由归纳假设和 T-IF 容易证明

定理：（保持）如果 Γ ├ t : T 且 t → t' 则 Γ ├ t' : T

练习：Γ ├ t' : T 以及 t → t' 是否蕴含 Γ ├ t : T ？

反例 (λx : Bool. λy : Bool . y)(true true) 是不良类型的，但是可以归约出 λy : Bool . y

Curry-Howard 对应

在无类型算术表达式中提及：算符 → 有两种类型规则：

• 引入规则 T-ABS，描述类型的元素是如何产生的

• 消去规则 T-APP，描述类型的元素是如何使用的

比如：习题：Figure 8-1 中哪些是引入规则？哪些是消去规则？

引入规则：T-TRUE T-FALSE，消去规则 T-IF

当一个引入形式 (λ) 是一个消去形式的直接子项时，将形成一个可归约表达式 redex

在构造逻辑中，命题 P 的证明需要具体的证据，这具有很强的计算性 computational feel

简单类型lambda 演算的一项可以看作对应它的类型的逻辑命题的一个证明；而归约则对应逻辑运算中用来化简证明的逻辑操作————切割消除推理 cut elimination

抹除和类型

大部分程序语言的编译器避免在运行时带上类型注释；类型注释只在类型检查时被使用，并不在编译后的内容中出现；实际上，程序被转化回到无类型的形式

这种转化可以用抹除函数 erasure function 来描述，抹除函数建立了有类型项到无类型项之间的映射

定义：（抹除函数）

定理：（抹除不影响求值）

定义：（抹除的逆）