3-Untyped Arithmetic Expressions
导论
这一章节和下一章节构建了一套工具服务于仅含布尔值和数值的小型语言
这个小型语言非常简单，但是可以承载几个非常重要的概念
- 抽象语法
abstract syntax - 归纳定义和证明
inductive definitions and proofs - 求值
evaluation - 运行时错误
runtime error
这个小型语言用到以下几个语法，字母 t 表示项 terms
在目前这个语言中，一个程序 program 就是可以从上述的语法构建出来的一个项，举个例子：
if false then 0 else 1;
> 1
在接下来的讨论中，出于方便阅读的考虑，复合参数将用括号 ( 来区分优先级；但是这个语言目前并没有二义性 ambiguity，括号引入与否并不影响程序的解释，举例
iszero(pred(succ 0));
> true
# 实际上写成无括号的形式也不影响求值
iszero pred succ 0;
> true
可能会出现奇怪的程序，比如 succ true，这个问题（指此类无意义的程序）将会由之后引入的类型系统解决
语法
对于语法有如下的归纳定义
定义：项的集合是最小的集合T，满足：
1. {true, false, 0} ⊆ T ;
2. if t1 ∈ T , then {succ t1, pred t1, iszero t1} ⊆ T ;
3. if t1 ∈ T , t2 ∈ T , and t3 ∈ T , then if t1 then t2 else t3 ∈ T .
“最小的”在这里指没有不被这三句包括的其他项
对于语法有以下等价的定义，这里提出这个定义是为了引入推导规则与推导符号—————————
还有一种基于集合运算的定义：
练习题不放了，懒得做 😦
为了证明这几种定义是等价的，需要证明S = T
命题： S = T
证明：（思路）通过证明 S ∈ T；T ∈ S证明两集合等价
项上的归纳
这一部分做出了一些对于项的归纳定义和证明
定义：项上的常量集合记为Consts：
Consts(true) = {true}
Consts(false) = {false}
Consts(0) = {0}
Consts(succ t1) = Consts(t1)
Consts(pred t1) = Consts(t1)
Consts(iszero t1) = Consts(t1)
Consts(if t1 then t2 else t3) = Consts(t1) ∪ Consts(t2) ∪ Consts(t3)
定义：项的长度记为 size，即抽象语法树中的所有节点个数
size(true) = 1
size(false) = 1
size(0) = 1
size(succ t1) = size(t1) + 1
size(pred t1) = size(t1) + 1
size(iszero t1) = size(t1) + 1
size(if t1 then t2 else t3) = size(t1) + size(t2) + size(t3) + 1
定义：项的深度记为 depth，既是抽象语法树的深度，也是满足 t ∈ Si 的最小 i
depth(true) = 1
depth(false) = 1
depth(0) = 1
depth(succ t1) = depth(t1) + 1
depth(pred t1) = depth(t1) + 1
depth(iszero t1) = depth(t1) + 1
depth(if t1 then t2 else t3) = max(depth(t1), depth(t2), depth(t3)) + 1
引理：项的常量集合的秩不大于项的长度，|Consts(t)| <= ssize(t)
证明：（证明思路）归纳证明，采用三角不等式进行放缩
直观上来说，一颗树的叶子节点个数当然不大于总结点个数
定理：（项上归纳原理）记 P 为项上的一个谓词，那么可以进行如下的归纳：
- 对深度的归纳：对所有
depth(r) <= depth(s)的项均有P(r)，那么可以归纳得到P(s)对所有s均成立 - 对长度的归纳：对所有
size(r) <= size(s)的项均有P(r)，那么可以归纳得到P(s)对所有s均成立 - 对结构的归纳：对所有
s的直接子项r均有P(r)，那么可以归纳得到P(s)对所有s均成立
这是对项的朴素归纳的一步延伸，可以简化归纳步骤
语义风格
没看懂
从我的理解出发，操作语义类似于LR语法分析，当前项代表一个机器状态，要么简化到达下一个状态，要么停止
求值
用 v 表示值 value
求值符号记为 →， t → t' 指 t 是状态机在某一时刻的状态，那么可以通过一步操作把状态设置为 t'
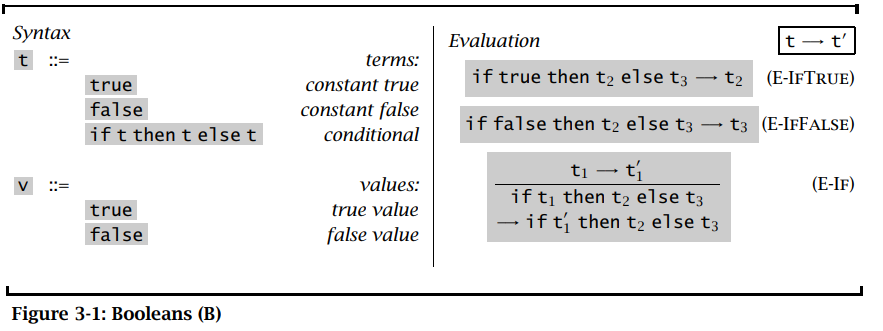
暂时只考虑布尔表达式的求值，下面列出了求值规则：
_ 前两个规则改变了句式结构，而后两个没有 _
与此同时，上述三个规则隐含的规定了求值顺序：首先简化（即图中用 t' 代换）条件 guard，直到简化为 true 或 false 再继续对条件求值；如果不这么做，很容易发现规则并没有定义 if t1 then t2 else t3 -> ?
为了更加精确（precise），我们定义求值关系如下：
定义：推导规则的一个实例 instance 是将处在规则的结论和前提相同的项代换元变量得到的结果
这段中英文都有点难理解，我的理解是这个定义规定了如何对求值规则使用代换原则
定义：A rule is satiefied by a relation if, for each instance of the rule, either the conclusion is in the relation or one of the premises is not.
第一次没有看懂，研究了一下知乎大佬的理解，下面贴出来
首先，relation 可以等同于 abstract machine 的状态转移函数。如果我们将程序的所有可能的语句定义为一个集合S，那么 relation 就是一个S → S的二元关系；这个二元关系将S中的某些语句（那些不是值的语句）映射到S中的另一些语句上，反映了 abstract machine 在单步执行某条语句后得到的新语句。其次，一条 rule 就是图 3-1 中在右列定义的一条推导规则。这一条定义则是说当 relation 的某个子集符合某一条 rule 所定义的推导规则时，我们可以称这个 relation 满足（satisfy）了某一条 rule。更加严格地，这一条定义还说明了我们应该如何考察 relation 是否满足某一条 rule。考察这一点需要 rule 的所有实例均满足两个条件中的一个：
- 如果 rule 实例的 conclusion 在 relation 中；
- 如果 rule 实例的某一条 premises 不在 relation 中。
转载自 https://zhuanlan.zhihu.com/p/403814280
定义：一步求值关系 → 是满足三个规则的项上最小的二元关系，对求值关系中的 (t, t')，称 t → t' 可推导出
这里的“最小”指 t → t'是可推导的，当且仅当它可由规则判断：要么是 E-IfTrue 或者 E-IfFalse 的一个实例，要么是 E-If 的一个实例的结论
定理：（一步求值的确定性）如果 t → t' 且 t → t''，那么 t' = t''
定义：范式 normal form 定义为如果没有求值规则可以作用于项 t，则 t 是一个范式，即不存在 t' 使得 t → t'
定理：t 是范式 iff t是一个值
这个定理仅在只讨论布尔表达式的情况下成立
定义：多步求值关系是单步求值关系的自反、传递闭包
定理：（范式唯一性）如果 t → u 且 t → u'，那么 u = u'
定理：（求值终止性）对每个项 t，存在范式 u 使 t → u
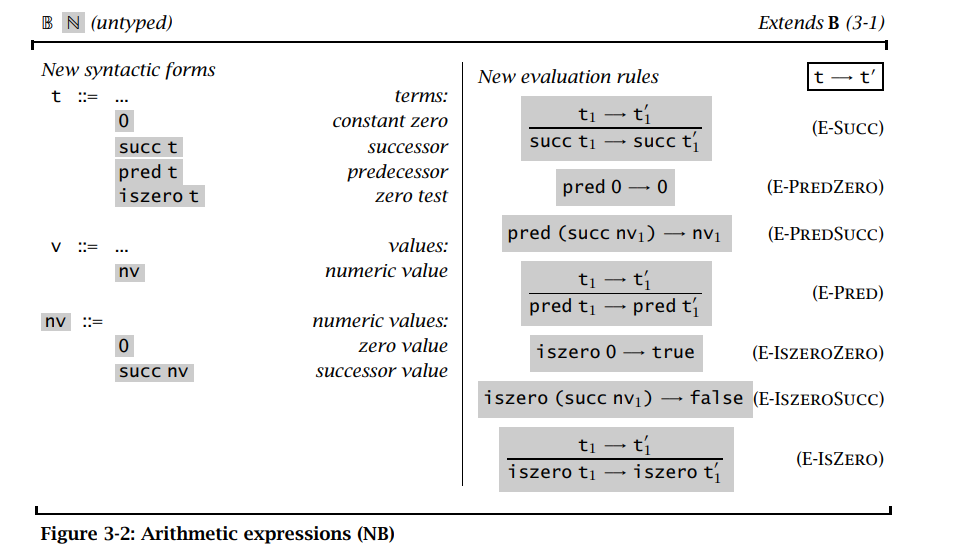
然后将求值规则扩展到数值
定义：如果一个封闭项是一个范式而不是一个值，则称此项受阻 stuck
比如 succ false
