DLX 学习笔记
Dancing Links X
用来解决精确覆盖问题以及他的一些变体
基础精确覆盖原型
栗子引入
给定一个由
组成的矩阵,是否能找到一个行的集合,使得集合中每一列都恰好包含一个
考虑如下矩阵:
先假定选择第1行,如下所示:
如上图中所示,红色的那行是选中的一行,这一行中有
由于这
根据定义,同一列的
就是选择一行, 找到所有
的位置, 再找到所有 的那一列, 把那一列中所有 所在的行删除
那么在接下来的求解中,红色的部分、黄色的部分、紫色的部分都不能用了,把这些部分都删除
得到一个新的矩阵
行分别对应矩阵
列分别对应矩阵
于是问题就转换为一个规模小点的精确覆盖问题
在新的矩阵中再选择第1行,如下图所示
还是按照之前的步骤,进行标示。红色、黄色和紫色的部分又全都删除,导致新的空矩阵产生,而红色的一行中有
那么回到之前,选择第
按照之前的步骤,进行标示。把红色、黄色、紫色部分删除后,得到新的矩阵
行对应矩阵
列对应矩阵
由于剩下的矩阵只有
于是该问题的解就是矩阵
在求解这个问题的过程中,我们第
开始抽象化
从上面的求解过程来看,实际上求解过程可以如下表示
1、从矩阵中选择一行
2、根据定义,标示矩阵中其他行的元素
3、删除相关行和列的元素,得到新矩阵
4、如果新矩阵是空矩阵,并且之前的一行都是
5、说明之前的选择有误,回溯到之前的一个矩阵,跳转到1;如果没有矩阵可以回溯,说明该问题无解,跳转到7
6、求解结束,把结果输出
7、求解结束,输出无解消息
从如上的求解流程来看,在求解的过程中有大量的缓存矩阵和回溯矩阵的过程。而如何缓存矩阵以及相关的数据(保证后面的回溯能正确恢复数据),也是一个比较头疼的问题(并不是无法解决)。以及在输出结果的时候,如何输出正确的结果(把每一步的选择转换为初始矩阵相应的行)。
于是算法大师 Donald E.Knuth出面解决了这个方面的难题。他提出了 DLX(Dancing Links X) 算法。实际上,他把上面求解的过程称为X算法,而他提出的舞蹈链(Dancing Links)实际上并不是一种算法,而是一种数据结构。一种非常巧妙的数据结构,他的数据结构在缓存和回溯的过程中效率惊人,不需要额外的空间,以及近乎线性的时间。而在整个求解过程中,指针在数据之间跳跃着,就像精巧设计的舞蹈一样,故Donald E.Knuth把它称为Dancing Links(中文译名舞蹈链)。
Dancing Links 的核心是基于双向链的方便操作(移除 和 恢复加入)
我们用例子来说明
假设双向链的三个连续的元素,A1、A2、A3,每个元素有两个分量 Left 和 Right,分别指向左边和右边的元素。由定义可知A1.Right=A2 ,A2.Right=A3, A2.Left=A1,A3.Left=A2
在这个双向链中,可以由任一个元素得到其他两个元素,A1.Right.Right=A3,A3.Left.Left=A1等等
现在把 A2 这个元素从双向链中移除(不是删除)出去,那么执行下面的操作就可以了 A1.Right=A3,A3.Left=A1
那么就直接连接起 A1 和 A3 。A2 从双向链中移除出去了。但仅仅是从双向链中移除了,A2 这个实体还在,并没有删除。只是在双向链中遍历的话,遍历不到 A2 了。
那么 A2 这个实体中的两个分量 Left 和 Right 指向谁?
由于实体还在,而且没有修改 A2 分量的操作,那么A2的两个分量指向没有发生变化,也就是在移除前的指向。即 A2.Left=A1 和 A2.Right=A3
如果此时发现,需要把 A2 这个元素重新加入到双向链中的原来的位置,也就是 A1 和 A3 的中间。由于 A2 的两个分量没有发生变化,仍然指向 A1 和 A3 。那么只要修改 A1 的 Right 分量和 A3 的 Left 就行了。也就是 A1.Right=A2,A3.Left=A2
仔细想想,上面两个操作(移除和恢复加入)对应了什么?是不是对应了之前的算法过程中的关键的两步?
移除操作对应着缓存数据、恢复加入操作对应着回溯数据。而美妙的是,这两个操作不再占用新的空间,时间上也是极快速的
实现
Dancing Links用的数据结构是交叉十字循环双向链
而Dancing Links中的每个元素不仅是横向循环双向链中的一份子,又是纵向循环双向链的一份子。
因为精确覆盖问题的矩阵往往是稀疏矩阵(矩阵中,
Dancing Links中的每个元素有
分别:Left 指向左边的元素、Right 指向右边的元素、Up 指向上边的元素、Down 指向下边的元素、Col 指向列标元素、Row 指示当前元素所在的行
Dancing Links还要准备一些辅助元素(为什么需要这些辅助元素?没有太多的道理,大师认为这能解决问题,实际上是解决了问题)
Ans[]:Ans数组,在求解的过程中保留当前的答案,以供最后输出答案用。
Head 元素:求解的辅助元素,在求解的过程中,当判断出 Head.Right=Head(也可以是 Head.Left=Head)时,求解结束,输出答案。Head 元素只有两个分量有用。其余的分量对求解没啥用
C 元素:辅助元素,称列标元素,每列有一个列标元素。本文开始的题目的列标元素分别是 C1、C2、C3、C4、C5、C6、C7。每一列的元素的 Col 分量都指向所在列的列标元素。列标元素的 Col 分量指向自己(也可以是没有)。在初始化的状态下,Head.Right=C1 、C1.Right=C2、……、C7.Right=Head、Head.Left=C7 等等。列标元素的分量 Row=0,表示是处在第
根据原矩阵:
构建交叉十字循环双向链(构建的过程后面的详述)

就上图解释一下
每个绿色方块是一个元素,其中 Head 和 C1、C2、……、C7 是辅助元素。橙色框中的元素是原矩阵中1的元素,给他们标上号(从
左侧的红色,标示的是行号,辅助元素所在的行是
每两个元素之间有一个双向箭头连线,表示双向链中相邻两个元素的关系(水平的是左右关系、垂直的是上下关系)
单向的箭头并不是表示单向关系,而因为是循环双向链,左侧的单向箭头和右侧的单向箭头(上边的和下边的)组成了一个双向箭头,
例如元素14左侧的单向箭头和元素16右侧的单项箭头组成一个双向箭头,表示 14.Left=16、16.Right=14;
同理,元素14下边的单项箭头和元素C4上边的单向箭头组成一个双向箭头,表示 14.Down=C4、C4.Up=14
接下来,利用图来解释Dancing Links是如何求解精确覆盖问题
1
1、首先判断是否 Head.Right=Head
- 若是,那就意味着是空矩阵了, 求解结束,输出解(也可以判断是否
Head.Left=Head) - 若不是,求解还没结束,到步骤2
2
2、获取 Head.Right 元素,即元素 C1,并标示元素 C1
(标示元素C1,指的是标示 C1、和 C1 所在列的所有元素、以及该元素所在行的元素,并从双向链中移除这些元素)。如下图中的紫色部分。
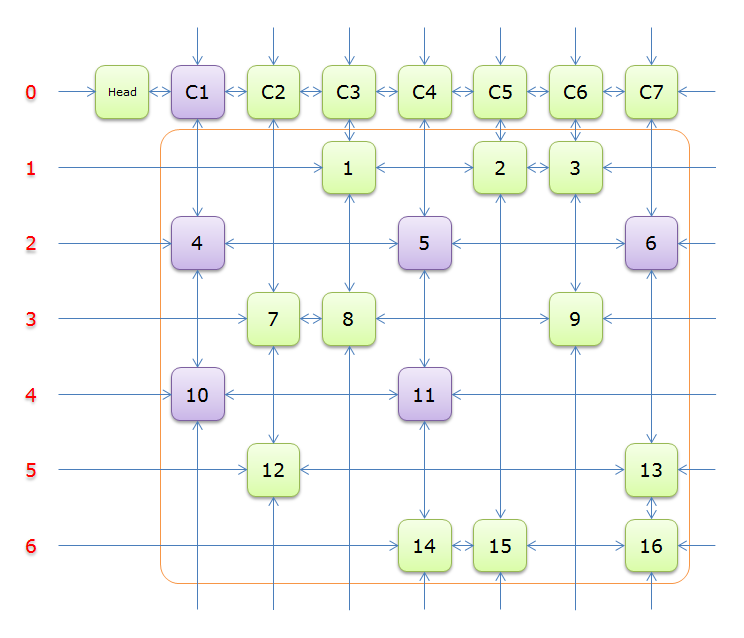
如上图可知,行 C1),先假设选择的是行
3
3、选择行 C4和标示元素 C7,下图中的橙色部分。
注意的是,即使元素 Col 分量还是指向元素 C4的,这里体现了双向链的强大作用。
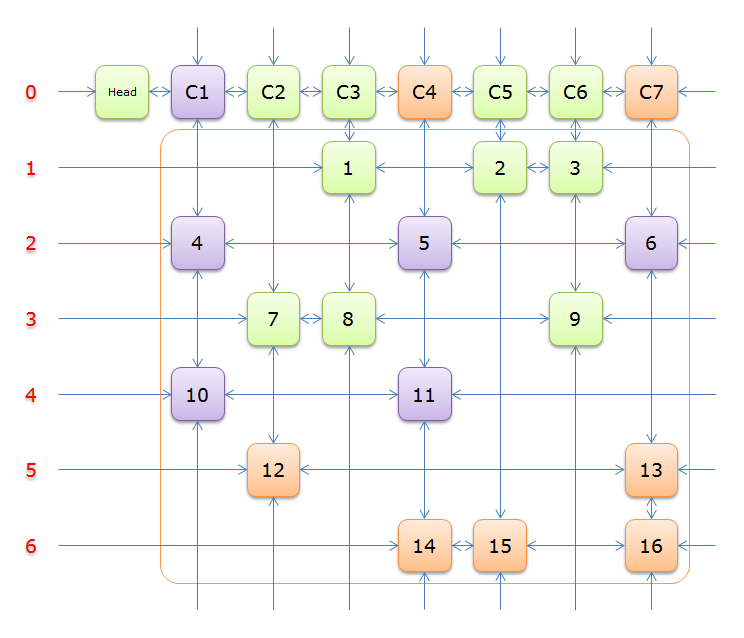
第
把上图中的紫色部分和橙色部分移除的话,剩下的绿色部分就如下图所示
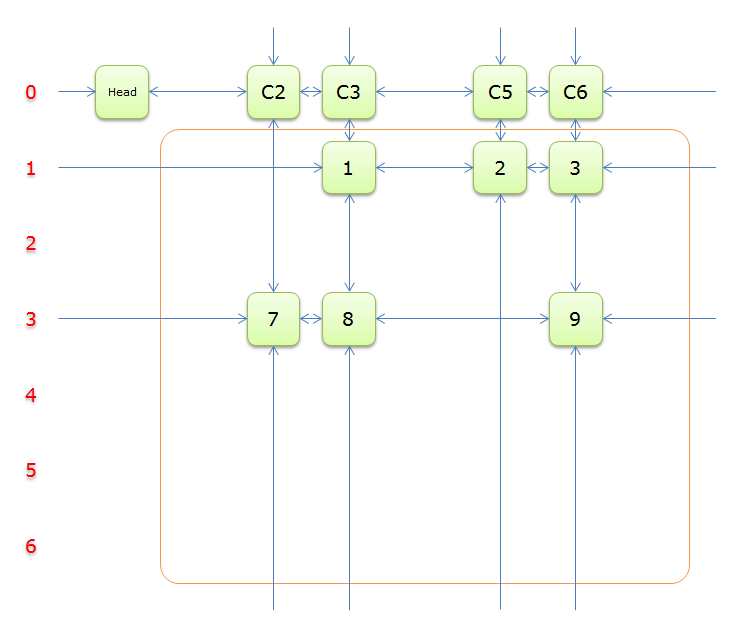
一下子空了好多,是不是转换为一个少了很多元素的精确覆盖问题?,利用递归的思想,很快就能写出求解的过程来。我们继续完成求解过程
4
4、获取Head.Right元素,即元素C2,并标示元素C2。如下图中的紫色部分。

如图,列C2只有元素 7 覆盖,故答案只能选择行
5
5、选择行 8 和元素 9)所在的列首元素,即标示元素C3和标示元素C6,下图中的橙色部分。
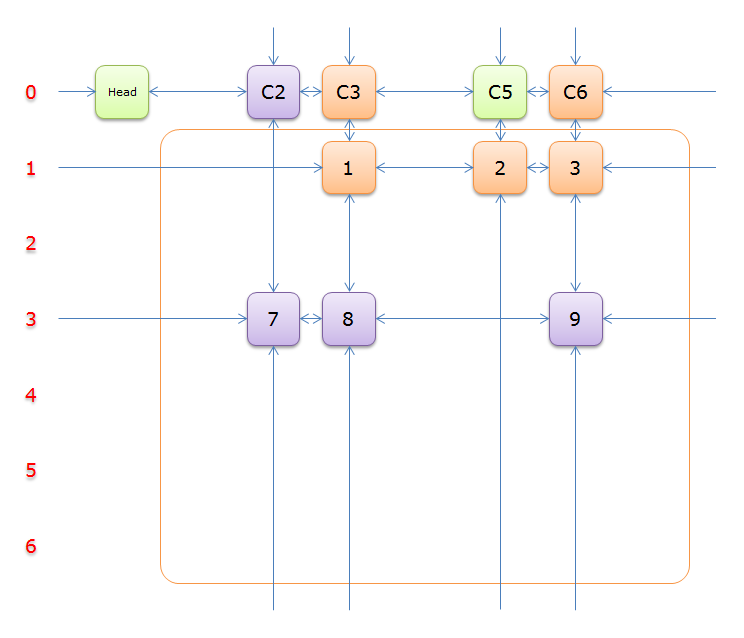
把上图中的紫色部分和橙色部分移除的话,剩下的绿色部分就如下图所示

6
6、获取 Head.Right 元素,即元素C5,元素C5中的垂直双向链中没有其他元素,也就是没有元素覆盖列C5。说明当前求解失败。要回溯到之前的分叉选择步骤(步骤2)。
那要回标列首元素(把列首元素、所在列的元素,以及对应行其余的元素。并恢复这些元素到双向链中),回标列首元素的顺序是标示元素的顺序的反过来。
从前文可知,顺序是回标列首C6、回标列首C3、回标列首C2、回标列首C7、回标列首C4。表面上看起来比较复杂,实际上利用递归,是一件很简单的事。并把答案栈恢复到步骤

7
7、由于之前选择行 11)所在的列首元素,即标示元素C4,下图中的橙色部分。
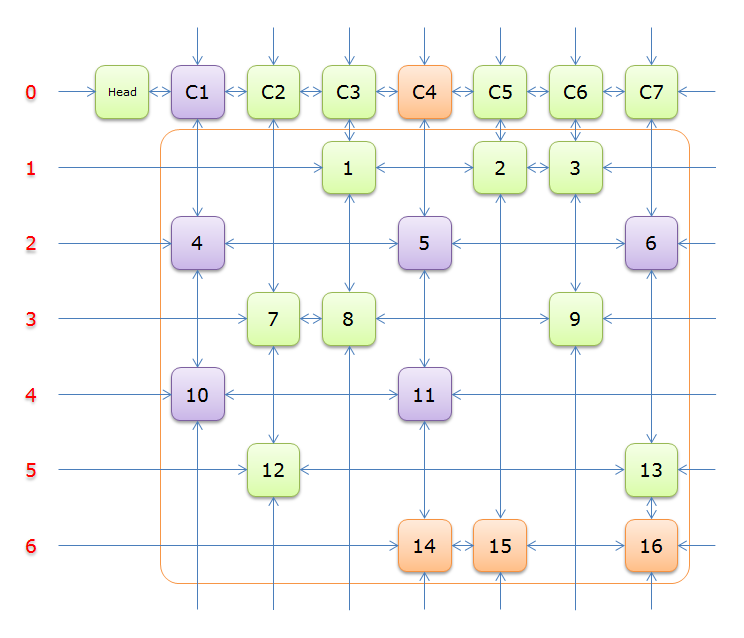
把上图中的紫色部分和橙色部分移除的话,剩下的绿色部分就如下图所示

8
8、获取Head.Right元素,即元素C2,并标示元素C2。如下图中的紫色部分。
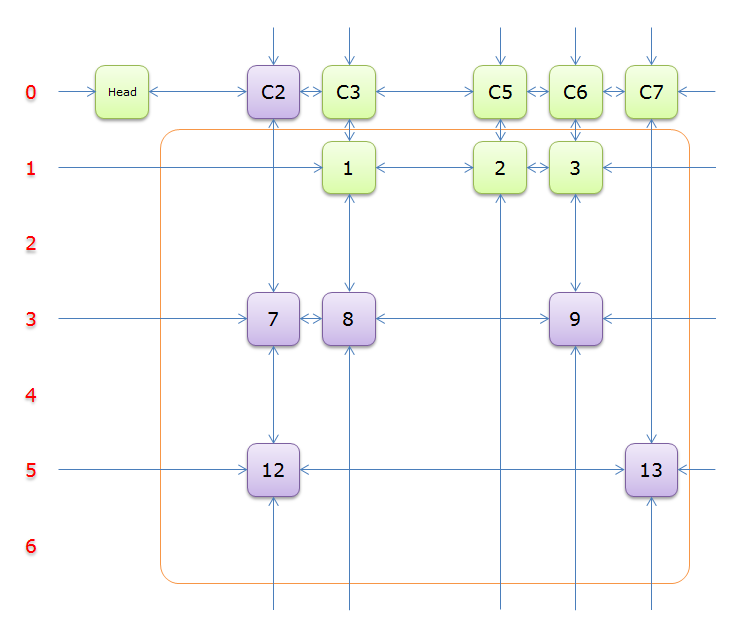
如图,行
9
9、选择行 8和元素9)所在的列首元素,即标示元素C3和标示元素C6,下图中的橙色部分
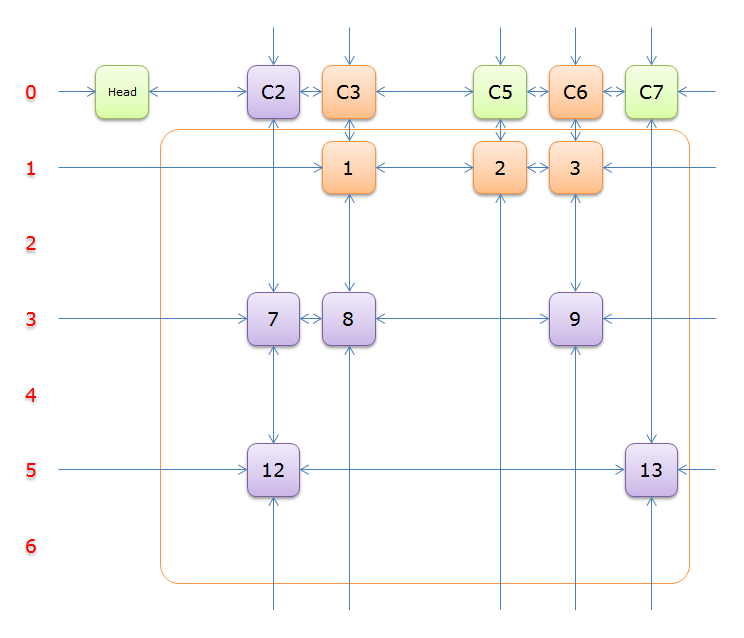
把上图中的紫色部分和橙色部分移除的话,剩下的绿色部分就如下图所示
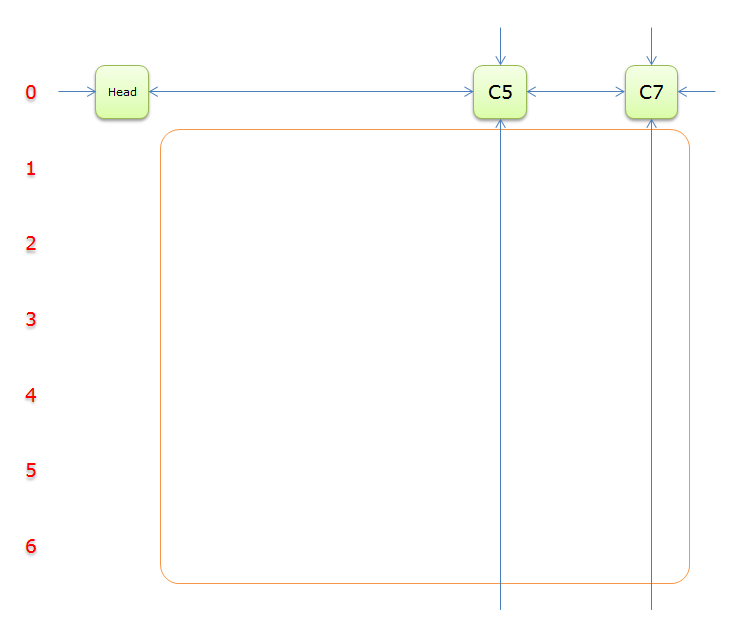
10
10、获取Head.Right元素,即元素C5,元素C5中的垂直双向链中没有其他元素,也就是没有元素覆盖列C5。说明当前求解失败。
要回溯到之前的分叉选择步骤(步骤 C6、回标列首C3。并把答案栈恢复到步骤

11
11、由于之前选择行 13)所在的列首元素,即标示元素 C7,下图中的橙色部分。
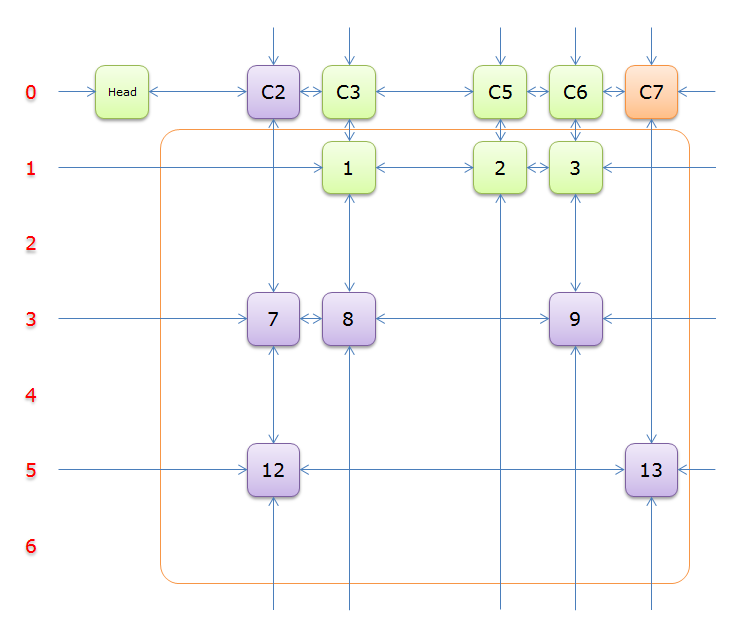
把上图中的紫色部分和橙色部分移除的话,剩下的绿色部分就如下图所示
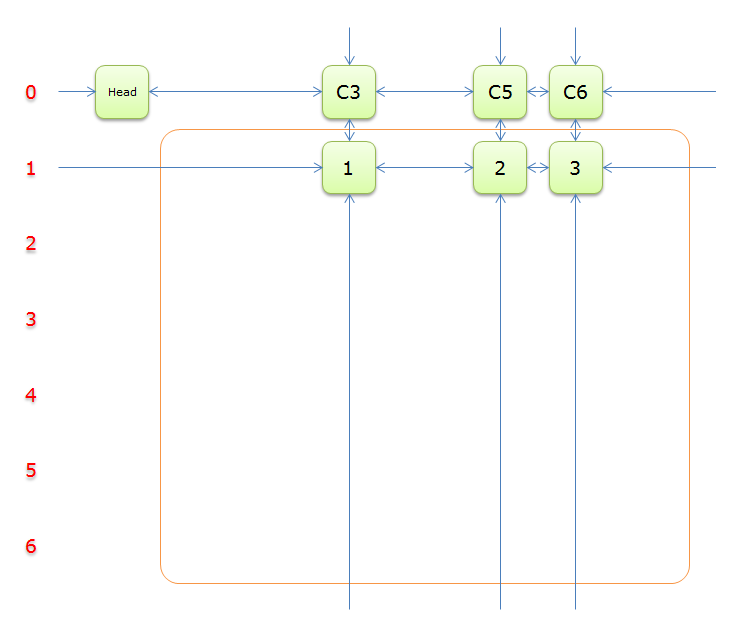
12
12、获取Head.Right元素,即元素C3,并标示元素C3。如下图中的紫色部分。
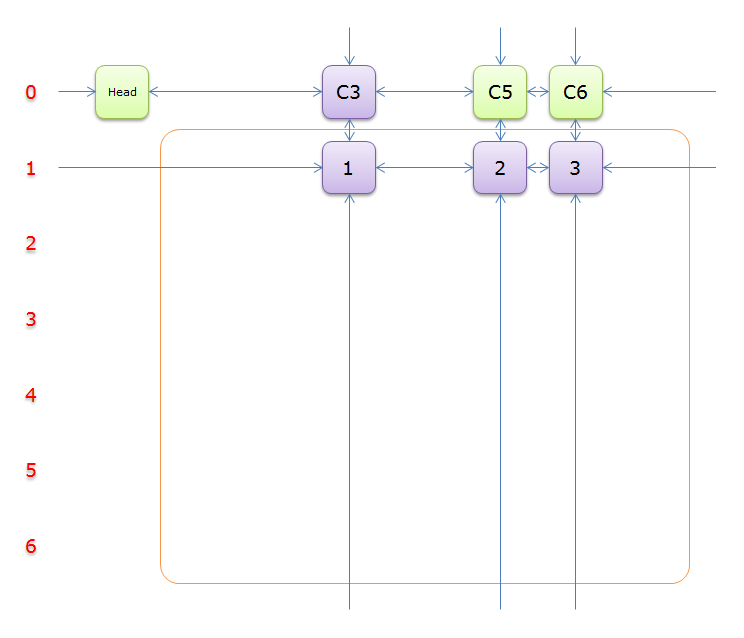
13
13、如上图,列C3只有元素1覆盖,故答案只能选择行 2和元素3)所在的列首元素,即标示元素C5和标示元素C6,下图中的橙色部分。
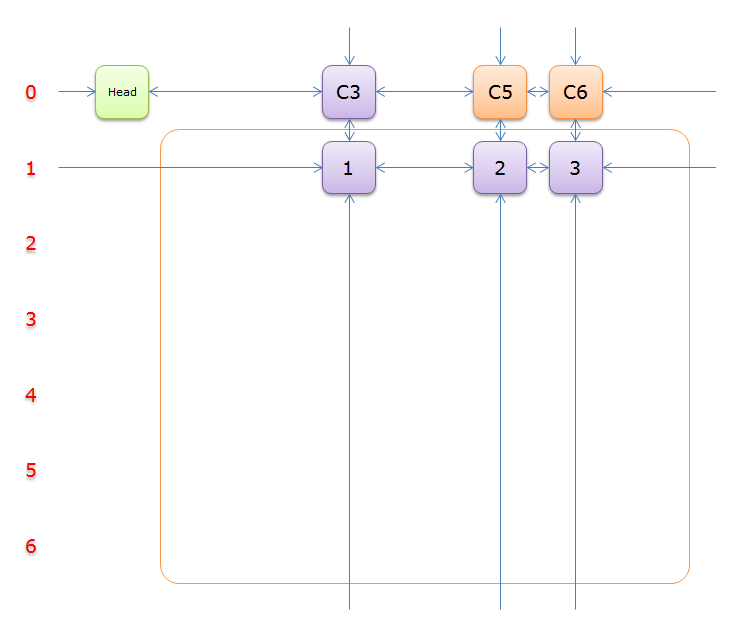
把上图中的紫色部分和橙色部分移除的话,剩下的绿色部分就如下图所示
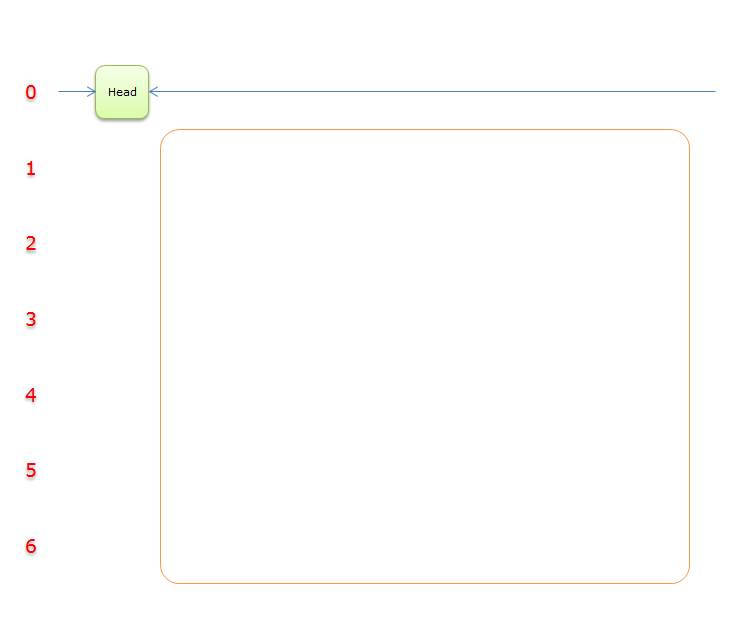
14
14、因为Head.Right=Head。故,整个过程求解结束。
输出答案,答案栈中的答案分别是
如下图所示(蓝色的部分)

所以, 删除
C是用来表示当前列已经被覆盖到了, 而删除行是因为与当前选择有冲突, 不可能选择他了
小总结
从以上的
Dancing函数的入口- 判断是否
Head.Right==Head若是,输出答案,返回True,退出函数。 - 获得
Head.Right的元素C - 标示元素
C - 获得元素
C所在列的一个元素 - 标示该元素同行的其余元素所在的列首元素
- 获得一个简化的问题,递归调用
Dancing函数,
- 若返回的是
True,则返回True,退出函数。 - 若返回的是
False,则回标该元素同行的其余元素所在的列首元素,回标的顺序和之前标示的顺序相反
- 获得元素
C所在列的下一个元素
- 若有,跳转到步骤
- 若没有,回标元素
C,返回False,退出函数。
相关题目
Luogu P4929 【模板】舞蹈链(DLX)
原题链接
思路
模板题
没啥说的
蒟蒻代码
结构体版
#include <bits/stdc++.h>
#define re register
#define rep(i,a,b) for(re int i=a;i<=b;i++)
#define per(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
struct DLXnode{
int row; // 当前点所在的行
int col; // 当前点所在列
int l; // 左边节点
int r; // 右边节点
int u; // 上面节点
int d; // 下面节点
};
const int N=505;
int n,m;
DLXnode node[N*N]; // 双向十字链表
int cnt=0; // 总节点数
int first[N]; // 每一行第一个节点
int col_cnt[N]; // 每列的节点数
int ans[N]; // 答案
// 初始化空矩阵
void init(){
rep(i,0,m){
node[i].l=i-1;
node[i].r=i+1;
node[i].u=node[i].d=i;
col_cnt[i]=0;
}
// 循环链表
node[0].l=m;
node[m].r=0;
cnt=m;
}
// 插入节点
void insert(int row,int col){
node[++cnt].col=col;
node[cnt].row=row;
// 先处理列, 因为列已经初始化过了, 不需要分类讨论
// 列链表插入在链表尾部
node[cnt].d=col;
node[cnt].u=node[col].u;
node[node[cnt].u].d=cnt;
node[col].u=cnt;
// 处理行
// 行链表也是插在链表尾部
if(!first[row]){ // 成为这行的第一个节点
node[cnt].l=node[cnt].r=cnt;
first[row]=cnt;
}else{ // 节点不是这个行链表的第一个元素
node[cnt].l=node[first[row]].l;
node[cnt].r=first[row];
node[node[cnt].r].l=cnt;
node[node[cnt].l].r=cnt;
}
col_cnt[col]++;
}
// 删除: 1.列链表 2.列链表元素所对应的行链表
void remove(int col){
// 删除行: 通过列链表来删除行
for(re int i=node[col].d;i!=col;i=node[i].d) // 枚举列节点
for(re int j=node[i].r;j!=i;j=node[j].r){
node[node[j].u].d=node[j].d;
node[node[j].d].u=node[j].u;
col_cnt[node[j].col]--;
}
// 删除列: 通过行链表来删除列, 直接删除列的辅助节点
node[node[col].l].r=node[col].r;
node[node[col].r].l=node[col].l;
}
// 恢复 与删除的顺序完全相反
void resume(int col){
// 恢复列链表
node[node[col].l].r=col;
node[node[col].r].l=col;
// 恢复行链表
for(re int i=node[col].d;i!=col;i=node[i].d)
for(re int j=node[i].r;j!=i;j=node[j].r){
node[node[j].u].d=j;
node[node[j].d].u=j;
col_cnt[node[j].col]++;
}
}
// 让链起舞
bool dance(int dep/*删了dep-1列*/){
if(!node[0].r){ // 空了, 表示成功
rep(i,1,dep-1) cout<<ans[i]<<" ";
return 1;
}
// 列是肯定要删光的, 关键问题在于选择哪几行, 所以, dfs的情况数是枚举行
int c=node[0].r; // 选超级节点的列节点最少的列
for(re int i=node[0].r;i;i=node[i].r)
if(col_cnt[i]<col_cnt[c])
c=i;
remove(c);
for(re int i=node[c].d;i!=c;i=node[i].d){ // 枚举剩下的行
ans[dep]=node[i].row; // 假设这行在答案里面, 加入答案
for(re int j=node[i].r;j!=i;j=node[j].r)
remove(node[j].col);
if(dance(dep+1)) return 1;
for(re int j=node[i].r;j!=i;j=node[j].r)
resume(node[j].col); // 恢复
}
resume(c);
return 0;
}
int main()
{
ios::sync_with_stdio(0);
clock_t c1 = clock();
#ifdef LOCAL
freopen("data.in","r",stdin);
freopen("data.out","w",stdout);
#endif
// ======================================================================
cin>>n>>m;
init();
rep(i,1,n)
rep(j,1,m){
int tmp; cin>>tmp;
if(tmp) insert(i,j);
}
if(!dance(1)) puts("No Solution!");
// ======================================================================
end:
cerr << "Time Used:" << clock() - c1 << "ms" << endl;
return 0;
}
数组版
#include <bits/stdc++.h>
#define re register
#define rep(i,a,b) for(re int i=a;i<=b;i++)
#define per(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
const int N=250005;
int n,m;
int cnt=0;
int row[N],col[N],l[N],r[N],u[N],d[N];
int first[N];
int ccnt[N]; // column count
int ans[N];
void init(){
rep(i,0,m){
l[i]=i-1;
r[i]=i+1;
u[i]=d[i]=i;
ccnt[i]=0;
}
l[0]=m; r[m]=0;
cnt=m;
}
void insert(int rr,int cc){
cnt++;
ccnt[cc]++;
row[cnt]=rr;
col[cnt]=cc;
u[cnt]=u[cc];
d[cnt]=cc;
u[cc]=cnt;
d[u[cnt]]=cnt;
if(!first[rr]){
l[cnt]=r[cnt]=cnt;
first[rr]=cnt;
}else{
l[cnt]=l[first[rr]];
r[cnt]=first[rr];
l[first[rr]]=cnt;
r[l[cnt]]=cnt;
}
}
void remove(int cc){
// 先删行
for(re int i=d[cc];i!=cc;i=d[i])
for(re int j=r[i];j!=i;j=r[j]){
d[u[j]]=d[j];
u[d[j]]=u[j];
ccnt[col[j]]--;
}
// 删列
r[l[cc]]=r[cc];
l[r[cc]]=l[cc];
}
void resume(int cc){
r[l[cc]]=cc;
l[r[cc]]=cc;
for(re int i=d[cc];i!=cc;i=d[i])
for(re int j=r[i];j!=i;j=r[j]){
d[u[j]]=j;
u[d[j]]=j;
ccnt[col[j]]++;
}
}
// 选择了 dep-1 行
bool dance(int dep){
if(!r[0]){
rep(i,1,dep-1) cout<<ans[i]<<" ";
return 1;
}
// 使搜索树最小
int c=r[0];
for(re int i=r[0];i;i=r[i])
if(ccnt[i]<ccnt[c])
c=i;
remove(c);
for(re int i=d[c];i!=c;i=d[i]){
ans[dep]=row[i];
for(re int j=r[i];j!=i;j=r[j]) remove(col[j]);
if(dance(dep+1)) return 1;
for(re int j=r[i];j!=i;j=r[j]) resume(col[j]);
}
resume(c);
return 0;
}
int main()
{
ios::sync_with_stdio(0);
clock_t c1 = clock();
#ifdef LOCAL
freopen("data.in","r",stdin);
freopen("data.out","w",stdout);
#endif
// ======================================================================
cin>>n>>m;
init();
rep(i,1,n)
rep(j,1,m){
int tmp; cin>>tmp;
if(tmp) insert(i,j);
}
if(!dance(1)) puts("No Solution!");
// ======================================================================
end:
cerr << "Time Used:" << clock() - c1 << "ms" << endl;
return 0;
}
Luogu P1784 数独
原题链接
思路
咕咕咕
Luogu P1074 [NOIP2009 提高组] 靶形数独
原题链接
思路
咕咕咕
Luogu P4205 [NOI2005] 智慧珠游戏
原题链接
思路
咕咕咕
参考内容
https://www.cnblogs.com/grenet/p/3145800.html
https://www.luogu.com.cn/blog/SCP/solution-p4929
https://blog.csdn.net/qq_37582970/article/details/79965945
本文作者:咕噜咕噜酱
本文链接:https://www.cnblogs.com/syqwq/p/16206811.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步