Kosaraju 算法
一.算法简介
在计算科学中，Kosaraju算法（又称为 Sharir Kosaraju算法 ）是一个线性时间(linear time) 算法, 用于找到的有向图的强连通分量。它利用了一个事实，逆图（与各边方向相同的图形反转, transpose graph）与原始图有相同的强连通分量。
逆图(Tranpose Graph )
我们对逆图定义如下：
若 \(G\) 为原始图, 则 \(G\) 的逆图 \(G^T\) 为
\(G^T=(V, E^T)\)，其中 \(E^T=\{(u, v):(v, u)∈E\}\)
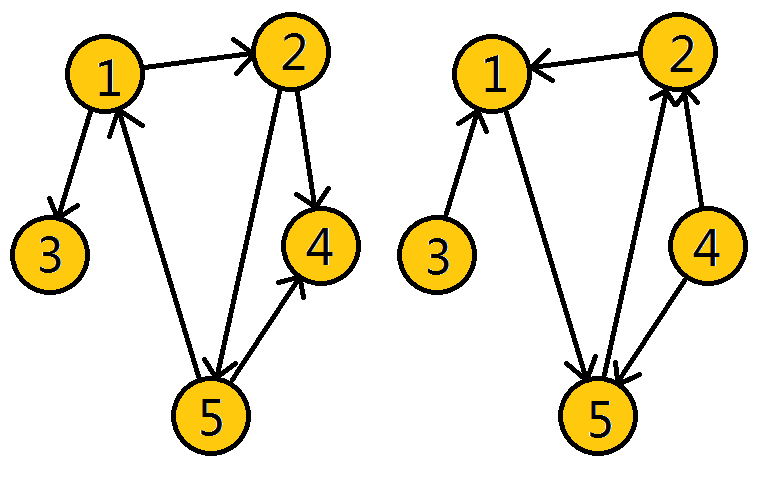
上图是有向图 \(G\) ， 和图 \(G\) 的逆图 \(G^T\)
通过以上的描述我们发现，Kosaraju 算法就是分别对原图 \(G\) 和它的逆图 \(G^T\) 进行两遍DFS，即：
-
.对原图 \(G\) 进行深度优先搜索，找出每个节点的完成时间(时间戳)
-
.选择完成时间较大的节点开始，对逆图 \(G^T\) 搜索，能够到达的点构成一个强连通分量
-
.如果 所有节点未都被遍历，重复2). ; 否则算法结束；
二.算法图示
上图是对图 \(G\) ,进行一遍DFS的结果，每个节点有两个时间戳，即节点的发现时间 u.d 和 完成时间 u.f
我们按照 结束时间戳 由小到大 压入栈中
-
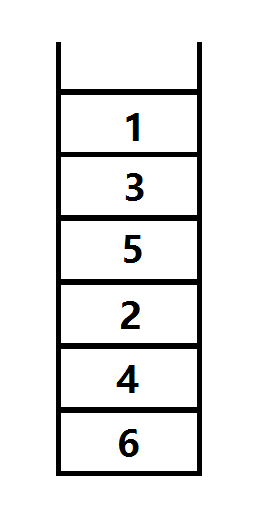
每次从栈顶取出元素
-
检查是否被访问过
-
若没被访问过，以该点为起点，对逆图进行深度优先遍历
-
否则返回第一步，直到栈空为止
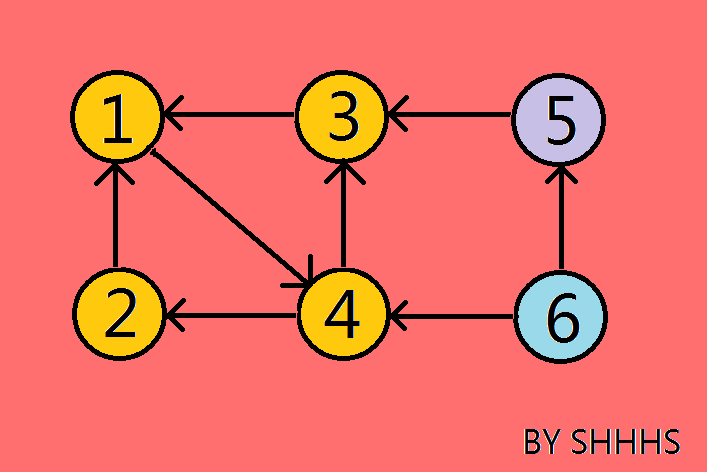
[ATTENTION]
对逆图搜索时，从一个节点开始能搜索到的最大区块就是该点所在的强连通分量。
从节点1出发，能走到 2 ，3，4 ， 所以{1 , 2 , 3 , 4 }是一个强连通分量
从节点5出发，无路可走，所以{ 5 }是一个强连通分量
从节点6出发，无路可走，所以{ 6 }是一个强连通分量
自此Kosaraju Algorithm完毕，这个算法只需要两遍DFS即可，是一个比较易懂的求强连通分量的算法。
三.算法复杂度
-
邻接表：\(O(V+E)\)
-
邻接矩阵：\(O(V^2)\)
该算法在实际操作中要比Tarjan算法要慢
四.算法模板&注释代码
#include <bits/stdc++.h>
using namespace std;
// 节点
struct node {
int next; // 下一个节点的索引位置
int to; // 当前节点的节点编号
};
const int N = 1e4 + 5; // 节点个数最大
const int M = 2e4 + 5; // 边的个数最大
int n, m;
// 因为是两张图 G 和 G^T 所以 统一加一维
// 数组模拟邻接表建图
int head[2][N];
node ver[2][M];
int cnt[2]; // 节点个数
int top = 0, sta[N]; // 栈顶指针 和 站 用来储存时间戳
bitset<N> vis;
int color[N]; // 染色数组, 用来记录哪些节点在一个连通块中
int sz[N]; // 各个连通块的大小
int tot = 0; // 连通块个数
int colorIndex = 0; // 颜色种类
// 加边(起点, 终点, 正图||逆图)
void addEdge(int x, int y, int _) {
ver[_][++cnt[_]].to = y;
ver[_][cnt[_]].next = head[_][x];
head[_][x] = cnt[_];
}
// 第一次 DFS 按照时间戳入栈
void firstDFS(int x, int _) {
vis[x] = 1;
for (int i = head[_][x]; i; i = ver[_][i].next) {
int y = ver[_][i].to;
if (vis[y]) continue;
firstDFS(y, _);
}
sta[++top] = x; // 结尾入栈
}
// 第二次 DFS 搜索 x 节点可以到达的点的集合, 即一个强连通块
void secondDFS(int x, int _) {
sz[tot]++;
vis[x] = 1;
color[x] = colorIndex; // 染色
for (int i = head[_][x]; i; i = ver[_][i].next) {
int y = ver[_][i].to;
if (vis[y]) continue;
secondDFS(y, _);
}
}
int main() {
ios::sync_with_stdio(0);
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
addEdge(u, v, 0); // G 加 正向边
addEdge(v, u, 1); // G^T 加 反向边
}
// 对原图的 DFS
for (int i = 1; i <= n; i++)
if (!vis[i]) firstDFS(i, 0);
vis &= 0; // 清空 vis[]
// 按时间戳对逆图进行 DFS
while (top > 0) {
int tmp = sta[top--];
if (vis[tmp]) continue;
tot++, colorIndex++;
secondDFS(tmp, 1);
}
// 输出 强连通块
for (int i = 1; i <= tot; i++) {
for (int j = 1; j <= n; j++)
if (color[j] == i) cout << j << " ";
cout << endl;
}
return 0;
}
