函数综合
函数综合
函数综合一、一些小概念1. 单调性判断单调性的方法单调性的应用*复合函数的单调性判断2. 奇偶性关于奇偶性奇偶性的应用*复合函数奇偶性3. 对称性对称性的本质对称性的分类4. 周期性周期性的本质具有周期性的抽象函数二、一些小练手三、一些小知识卡西欧 SOLVE 是如何解方程的牛顿法求解函数最值问题
一、一些小概念
1. 单调性
判断单调性的方法
定义法
已知函数 ,
- 则 在 上 单调递增
- 则 在 上 单调递减
- 求导
已知函数 , 在其定义域内均可导, 则有
- , 则 单调递增
- , 则 单调递减
- , 则 取到极值点.
定义法变形(类似导数定义)
已知函数 ,
- 若 ,则 在 上 单调递增
- 若 ,则 在 上 单调递减
单调性的应用
比较大小
(1) 利用单调性可以比较函数值的大小,即增函数中自变量大函数值也大,减函数中自变量小函数值反而变大;
(2) 利用函数单调性比较大小应注意将自变量放在同一单调区间.
解不等式
(1) 利用单调性解不等式就是利用函数在某个区间内的单调性,推出两个变量的大小,然后去解不等式.
(2) 利用单调性解不等式时应注意函数的定义域,即首先考虑使给出解析式有意义的未知数的取值范围.
(3) 利用单调性解不等式时,一定要注意变量的限制条件,以防出错.
*复合函数的单调性判断
简单证明:
若 , 且在定义域处处可导,则有,不难看出:
- 若 与 单调性相同,则 与 符号相同, 大于 0, 单调递增
- 若 与 单调性不同,则 与 符号相反, 小于 0, 单调递减
即 同增异减
2. 奇偶性
关于奇偶性
- 定义域关于 对称
- 则 为 奇函数
- 则 为 偶函数
- , 这个小技巧可以在小题目里取取巧
- 若奇函数 的定义域包含0, 切莫忘记写
奇偶性的应用
- 解不等式
*复合函数奇偶性
若 ,
若 为偶函数, , 为偶函数
若 为奇函数,
- 若 为奇函数,
- 若 为偶函数,
即 内偶则偶,内奇同外
3. 对称性
对称性的本质
对称性的本质就是奇偶性经过平移的结果, 由于平移方式的不同, 于是就造就了对称性的不同
对称性的分类
关于点对称 [奇函数 平移 ][中点坐标公式 ]
若 关于点对称,
则有, 整理得
关于轴对称 [偶函数 平移 ]
若关于对称, 则有
4. 周期性
周期性的本质
周期性的本质就是对称性复合的结果, 一个函数有两个及以上条对称轴, 于是就有了周期性
具有周期性的抽象函数
函数 对定义域内任意实数 满足 (其中 为常数)
- ,则 是以 为周期的周期函数
- ,则 是以 为周期的周期函数
- ,则 是以 为周期的周期函数
- ,则 是以 为周期的周期函数
- ,则 是以 为周期的周期函数
二、一些小练手
- 函数 的值域为__________________
- 已知 与 都是定义在 上的奇函数,且当 时, ,,若 ,恰有4个零点,则正实数 的取值范围是______________
关于函数 ,有下面四个结论:
(1) 是奇函数 (2) 当 时, 恒成立
(3) 的最大值是 (4) 的最小值是
其中正确结论的个数为 ( )
A. 1个 B. 2个 C.3个 D.4个
已知函数 的定义域为 ,对任意 都满足 ,当 时,
(1) 判断并证明 的单调性和奇偶性
(2) 是否存在这样的实数 ,当 时,使不等式 对所有 恒成立,如存在,求出 的取值范围;若不存在,说明理由
已知函数 的定义域是 ,且 , , 当 时,,
(1) 求证: 为奇函数
(2) 求 在区间 上的解析式
(3) 是否存在正整数 ,使得当 时,不等式 有解?请证明你的结论。
三、一些小知识
卡西欧 SOLVE 是如何解方程的
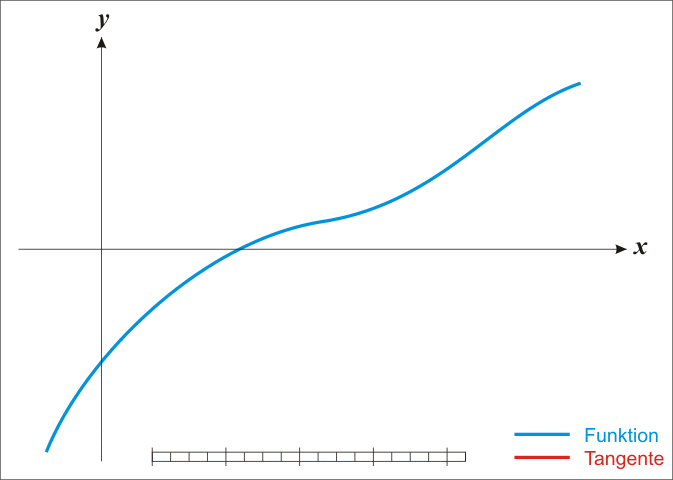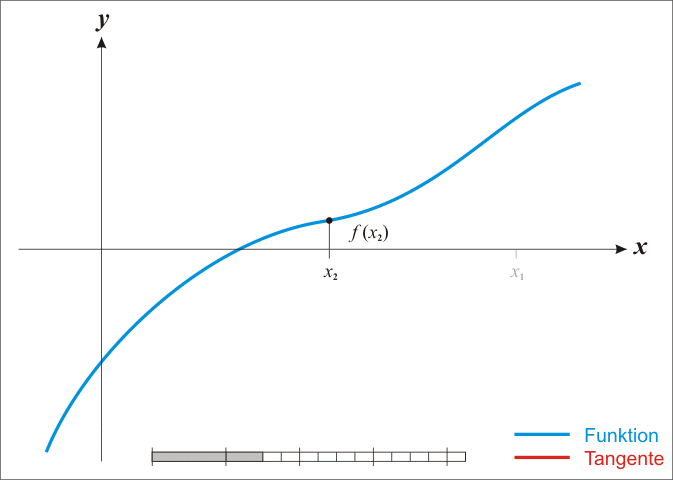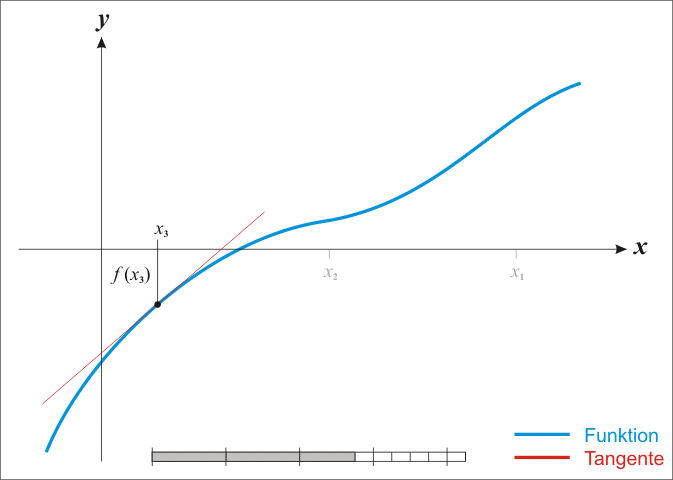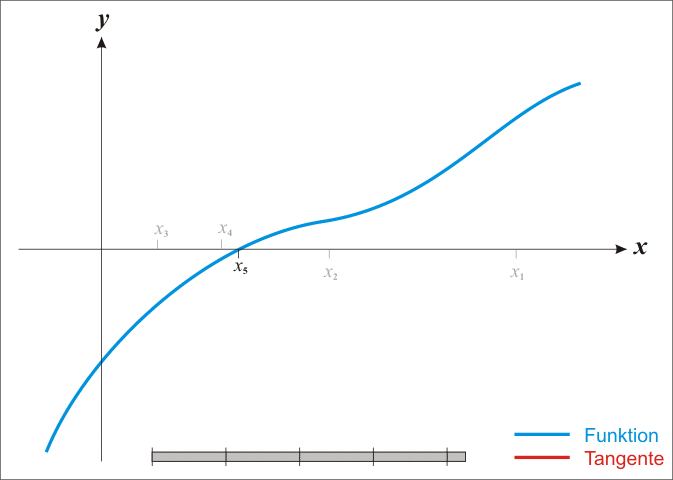
参阅说明书,会发现 “SOLVE 使用牛顿法得出方程的近似解” ,理解这一点会帮助我们更准确地,更完整地使用 SOLVE 这个功能。
这里提到一个求解方程的方法——牛顿法:
从根本上说,牛顿迭代法通过一系列的 迭代 操作使得到的结果 不断逼近 方程的实根。
首先,要选择一个初始值 ,使得该初始值接近实根的值。
然后,迭代计算如下的公式
直到 达到一个满意的近似结果为止。
牛顿法求解函数最值问题
牛顿法也被用于求函数的极值。由于函数取极值的点处的导数值为零,故可用牛顿法求导函数的零点,其迭代式为 . 求拐点的公式以此类推