矩阵快速幂解决斐波那契数问题
矩阵快速幂
定义:矩阵的快速幂是用来高效地计算矩阵的高次方的。
基础储备知识
线性代数中矩阵乘法
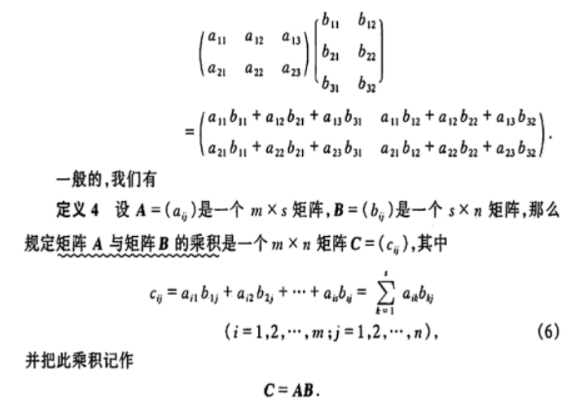
快速幂如果我们现在要算
x^8=x*x*x*x*x*x*x*x
$$
现在我们来优化其算法,我们先两两相乘,得到的结果再相乘四次
(x*x)^4
$$
相比第一次乘法运算7次,第二种方只需要运算4次;
我们知道计算机处理的是离散的信息,都是以0,1来作为信号的处理的。它能将模拟信号转化成数字信号,将原来连续的实际模型,用一个离散的算法模型来解决。回头看看矩阵的快速幂问题,我们是不是也能把它离散化呢?比如x8 = x8 * x2 * x1 显然采取这样的方式计算时因子数将是log(n)级别的(原来的因子数是n),不仅这样,因子间也是存在某种联系的,比如x4 能通过x2 * x2 得到,x8 能通过x4 * x4 得到,下面举个例子进行说明:
快速幂举例:计算x的11次方,x的11次方,11转换为二进制为1011,我们可以将其划分如下
x^{11}=x^{8}*x^{2}*x^1
$$
//初始化
ans = 1 ; res = x;
//1011最后一位是1,为奇数。
ans = res * ans = x;
res = res * res x^2;
//右移后,101最后一位是1,为奇数。
ans = res * ans = x^3;
res = res * res x^4;
//右移后,10最后一位是0,为偶数。
res = res * res x^8;
//右移后,1最后一位是1,为奇数。
ans = res * ans = x^11;
res = res * res x^16;
可以看出res=x^m ,m始终和二进制位置上的权值是对应的。当二进制位为0时,我们只让res * res使幂指数对应下一个二进制位的权值,当二进制位为1时,ans = ans * res 。则乘上了该乘的X幂次。
快速幂代码:
while(n){ //快速幂
if(n&1) //掩码00...01来判断最后位奇偶性
mult(C,B);
n>>=1; //右移一位
mult(B,B);
}
mult(A,C);
return A[0][0];
}
以斐波那契数列为例:斐波那契数列递推公式为: F[n] = F[n-1] + F[n-2]. 由f[0]=0,f[1]=1,可以递推后面的所有数。 通常,我们会常常用for循环,这是最直接的算法。 POJ 3070 题目,让求斐波那契数列,其n更是高达10亿。 但是直接递推存在局限性: (1)本题让你递推的斐波那契数n高达10亿。测试时间仅1秒的时间,递推方法显然会超时 (2)想要打表实现随机访问根本不可能,先把斐波那契数列求到10亿,然后想去进行随机访问。题目未给出那么多内存,数组也开不到10亿。
(3)使用滚动数组也会和递归一样会超时。
因此它可以用矩阵快速幂来写。 观察f[n] = f[n-1]+f[n-2] 第n相是由第n-1项和第n-2项递推而来。 同理,第n+1项由第n项和第n-1项递推而来。 因此可以用矩阵表示:
\left[\matrix {f(n) \\f(n-1) } \right]_1 = \left[ \matrix{ 1 & 1\\ 1 & 0\\ } \right]_2 * \left[\matrix {f(n-1) \\f(n-2) } \right]_3 = \left[ \matrix{ f(n-1)+f(n-2)\\ f(n-1) } \right]_4
$$
所以f(n) 位置位置上的值便是我们所想求的值。
class Solution{
public:
int fib(int n){
int A[2][2]={1,0,0,0};//求解矩阵,矩阵1
int B[2][2]={1,1,1,0};//工具矩阵,矩阵2
int C[2][2]={1,0,0,1};//单位矩阵
while(n){//快速幂
if(n&1)mult(C,B);
n>>=1;
mult(B,B);
}
mult(A,C);
return A[0][0];
}
private:
void mult(int ((*A)[2],int (*B)[2]){
int C[2][2]={0,0,0,0};
for(int k=0;k<2;++k)
for(int i=0;i<2;++i)
for(int j=0;j<2;++j)
C[i][j]+=A[i][k]*B[k][j];//矩阵乘法
for(int i=0;i<2;++i)
for(int j=0;j<2;++j)
A[i][j]=C[i][j];
}
};

