DS博客作业03-树
2020-04-12 13:28 pluto1214 阅读(201) 评论(0) 收藏 举报0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
串的概念:由有限个字符组成的序列
字串:串中任意个连续的字符组成的子序列
主串:包含字串的串
BF算法(又称古典的、穷举的)
特点:目标串上的指针需要不停地回溯,效率较差
KMP算法
特点:指针不需要回溯,匹配速度快
含义:定义一个next[j]数组,当主串字符op与子串失配时,op下回应和子串第next[j]个字符比较
改进KMP算法:由于next数组有缺陷例如主串为aaabaaaaaaaaaaaaaab,子串为aaaab,由于next[j]=k,而
子串中t[j]=t[k],所以当失配时,主串不用与t[k]进行比较,因而引入nextval[j]数组



二叉树的性质
1.非空二叉树上叶子节点树等于双分支节点数加1,即n0=n2+1
2.在二叉树的第i层上至多有2^(i-1)个节点(i>=1)
3.高度为h的二叉树至多有2^h-1个节点
二叉树存储结构
typedef struct Tnode
{
char/int data;
struct Tnode* lchild,rchild;
}BiTnode,*BTree;
二叉树的创建方法:
1.将二叉树的顺序存储结构转为二叉链 2.前序序列创建二叉树
BTree createTree(string s,int i) BTree createTree(string s,int& i)
{ {
if(i>=s.size或s[i]=='#')return NULL; if(i>=s.size)return NULL;
创建根节点B,B->data=s[i]; if(s[i]为#)i++,return NULL;
创建左子树:B->lchild=createTree(s,2*i); 创建根节点B,B->data=s[i];i++;
创建右子树:B->rchild=createTree(s,2*i+1); 创建左子树:B->lchild=createTree(s,i);
return B; 创建右子树:B->rchild=createTree(s,i);
} retirn B;
}
3.表达式建树
void InitExpTree(BTree& T, string str)
{
初始化数根栈tree,运算符栈s;
定义BTree T1,T2;
while(str[i]!='\0')
{
若str[i]为数字,则新建一棵以str[i]为数根的树,然后进数根栈;
若为运算符
栈顶运算符优先级小于str[i]或栈空,则将str[i]进运算符栈s
大于则从tree栈中弹出两棵树和从s中弹出一个运算符树生成一棵新树并进树栈
若等于则删除运算符栈的栈顶元素s.pop()
}
将运算符剩余元素弹出建树
}
4.括号法建树,前序和中序建树,中序和后序建树等
根据前序序列和中序序列建树
Tree create(char* pre, char* in, int n)
{
Tree s;
char* p;
int k;
if (n <= 0)
return NULL;
s = new BiTnode;
s->data = *pre;
for (p = in; p < in + n; p++)
{
if (*p == *pre)
break;
}
k = p - in;
s->lchild = create(pre + 1, in, k);
s->rchild = create(pre + k + 1, p + 1, n - k - 1);
return s;
}
根据后序序列和中序序列建树
Tree create(int* post, int* in, int n)
{
Tree s;
int* p;
int k;
if(n<=0)
{
return NULL;
}
s = new BiTnode;
s->data = *(post + n - 1);
for (p = in; p < in + n; p++)
{
if (*p == *(post + n - 1))
break;
}
k = p - in;
s->lchild = create(post, in, k);
s->rchild = create(post + k, p + 1, n - k - 1);
return s;
}
二叉树的遍历
void PreOrder(BTree T)//先序遍历 void InOrder(BTree T)//中序遍历 void PostyOrder(BTree T)//后序遍历
{ { {
if(T!=NULL) if(T!=NULL) if(T!=NULL)
{ { {
cout<<T->data; InOrder(T->lchild); PostOrder(T->lchild);
PreOrder(T->lchild); cout<<T->data; PostOrder(T->rchild);
PreOrder(T->rchild); InOrder(T->rchild); cout<<T->data;
} } }
} } }
二叉树的应用:
1.文档中的很多属性和项目靠树来爬取分析
2.求二叉树的高度,找某个值等
int GetHeight(BinTree BT)//求二叉树高度
{
int high1 = 0;
int high2 = 0;
if (BT == NULL)
return 0;
high1 = GetHeight(BT->Left)+1;
high2 = GetHeight(BT->Right)+1;
if (high1 > high2)//比较左右树高度的大小
return high1;
else
return high2;
}
3.将中缀表达式放入二叉树中,后序遍历二叉树可得后缀表达式
void InitExpTree(BTree& T, string str)
{
int i = 0;
stack<BTree> tree;//存放树根的栈
stack<char> s;//存放运算符的栈
BTree T1, T2;
char ch;
while (str[i] != '\0')
{
if (!In(str[i]))//是数字直接进树栈
{
T = new BTNode;
T->data = str[i];
T->lchild = NULL;
T->rchild = NULL;
tree.push(T);
i++;
}
else//是运算符
{
if (s.empty() || Precede(s.top(), str[i]) == '<')//栈空或者栈顶运算符优先级小于str[i]
{
s.push(str[i]);
i++;
}
else if (Precede(s.top(), str[i]) == '>')//栈顶运算符优先级大于str[i]
{
ch = s.top();//出栈一个运算符
s.pop();
T2 = tree.top();//出栈两棵树
tree.pop();
T1 = tree.top();
tree.pop();
CreateExpTree(T, T1, T2, ch);//生成一棵新树
tree.push(T);//将新生成的树入树栈
}
else//栈顶运算符优先级大于str[i]
{
s.pop();//出栈运算符栈
i++;
}
}
}
while (!s.empty())//若运算符栈不空,则出栈生成树
{
ch = s.top();
s.pop();
T2 = tree.top();
tree.pop();
T1 = tree.top();
tree.pop();
CreateExpTree(T, T1, T2, ch);
tree.push(T);
}
}
double EvaluateExTree(BTree T)
{
double a, b;
if (!T->lchild && !T->rchild)//叶子节点均为操作数
{
return T->data - '0';
}
a = EvaluateExTree(T->lchild);
b = EvaluateExTree(T->rchild);
switch (T->data)
{
case '+':return a + b;
case '-':return a - b;
case '*':return a * b;
case '/':
if (b == 0)
{
cout << "divide 0 error!";
exit(0);//除0错误,结束程序
}
return a / b;
}
}
树的一些术语和性质
1.根:即根节点,没有前驱
2.叶子:即终端节点,没有子树
3.森林:指m棵不相交的树的集合
4.有序树:节点从左到右有序,不能互换
5.无序树:节点各子树可互换位置
6.双亲:即上层的那个节点(直接前驱)
7.孩子:即下层节点的子树的根(直接后继)
8.兄弟:同一双亲下的同层节点
9.祖先:即从根到该节点所经分支的所有节点
10.子孙:即该节点下层子树中的任一节点
11.节点:即树的数据元素
12.度:节点的子树目,分支数目
13.节点的层次:从根到该节点的层数,根节点算一层
14.终端节点:即叶子
15.分支节点:即度不为的节点,也称为内部节点
16.树的深度:指所有节点中最大的层数
性质一:树中的节点树等于所有节点的度数之和加1
性质二:度为m的树的第i层上至多有m^(i-1)个节点(i>=1)
树的存储结构
双亲存储结构 孩子存储结构 孩子兄弟链存储结构
typedef struct typedef struct node typedef struct Tnode
{ { {
int data; int data; int data;
int parent; struct node*sons[MAXSons]; struct tnode*son;
}PTree[MAXSIZE]; }SonNode; struct tnode*brother;
缺点:找孩子不容易 缺点:找父亲不容易 }TSBnode;
缺点:找父亲不容易
遍历方法:
先根遍历:若树不空,先遍历根节点,然后依次先根遍历各棵子树
后根遍历:若树不空,则先依次后根遍历各棵子树,然后访问根节点
层次遍历:若树不空,自上而下,从左到右访问每个节点
树的应用:
1.目录树
2.二叉树转为树,树转为二叉树
3.查询重复率
线索二叉树
概念:二叉链存储结构时,每个节点有两个指针域,利用空链域,指向线性序列中的前驱和后继
存储结构
typedef struct Tnode
{
char/int data;
int ltag,rtag;
struct Tnode* lchild,rchild;
}BiTnode,*BTree;
当ltag=0时,lchild指向其左孩子
当ltag=1时,lchild指向其前驱
当rtag=0时,rchild指向其右孩子
当rtag=1时,rchild指向其前驱

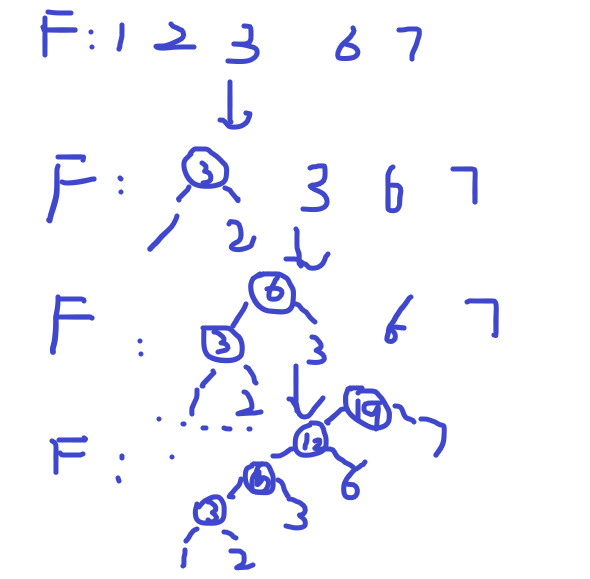
哈夫曼树:具有最小带权路径长度的树称为哈夫曼树
创建过程:在给定的n个权值(F=(T1,T2....Tn))中选取权值最小的两个权值作为左右孩子,
根节点为两个孩子的权值之和,再将新树放入F中,反复进行以上操作,最后当F中只剩一棵树时,
该树为哈夫曼树。
创建哈夫曼树过程如下


并查集
存储结构
typedef struct node
{
int data;
int rank;
int parent;
}UFSTree;
并查集树初始化 查找一个元素所属的集合
void Make_set(UFSTree t[],int n) int find(UFSTree t[],int x)
{ {
int i; if(x!=t[x].parent)
for(i=1;i<=n;i++) return find(t,t[x].parent);
{ else
t[i].data=i; return x;//双亲是自己
t[i].rank=0; }
t[i].parent=i;
}
}
两个元素所属集合的合并
void Union(UFSTree t[],int x,int y)
{
x=find(t,x);
y=find(t,y);
if(t[x].rank>t[y].rank)//y的秩小于x的秩
t[y].parent=x;//将y连到x节点上
else
{
t[x].parent=y;//将x连到y上
if(t[x].rank==t[y].rank)//相等
t[y].rank++;//y节点的秩增1
}
}
1.2.谈谈你对树的认识及学习体会。
树的内容比较多,有很多新的词语,比如叶子,根,度等,学习起来的时间大都比较长,编程难度也比较大,
由于树的创建遍历以及应用等大都需要递归,理解起来便更有难度了,不过通过编程之后可以慢慢理解,用心
学的话也会发现内容比较有趣
2.阅读代码
2.1 题目及解题代码
题目:相同的树


2.1.1 该题的设计思路
使用递归的方式同步遍历两棵树,开始先判断有无空树的情况,然后比较节点值的大小,最后再进行遍历即可。
2.1.2 该题的伪代码
bool isSameTree(TreeNode* p, TreeNode* q)
{
if树p和q都为空,return true;
else if树p和q只有一个为空,return false;
if节点值p->val!=q->val,return false;
递归遍历左树和右树
if(!isSameTree(p->left,q->left)) return false;
if(!isSameTree(p->right,q->right)) return false;
return true;
}
2.1.3 运行结果

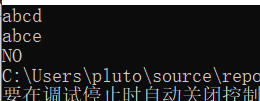
2.1.4分析该题目解题优势及难点。
解题优势:运用了递归的方法解题,代码简短,可读性好,而且虽然用了递归,但也好理解
难点:递归窗口的设计,对递归遍历树要比较熟悉
2.2 题目及解题代码
题目:对称二叉树

2.2.1 该题的设计思路
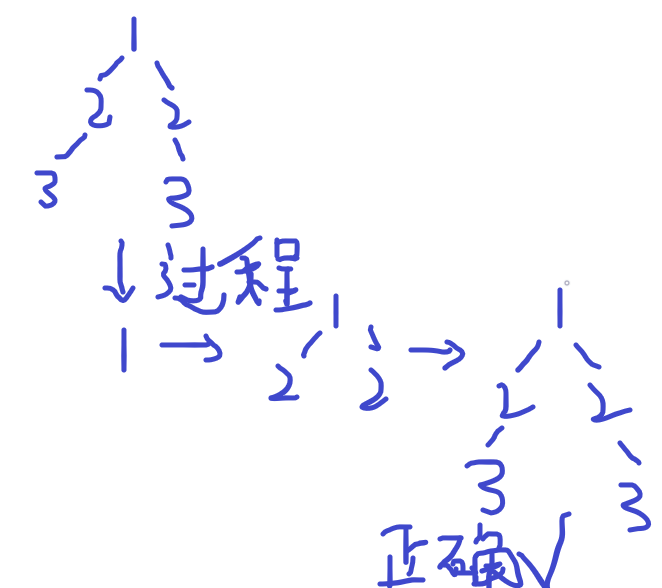
2.2.2 该题的伪代码
bool isSymmetric(TreeNode* root)
{
if(为空树) return true;
否则return isMirror(root->left,root->right);//判断是否镜像对称
}
bool isMirror(TreeNode *p,TreeNode *q)
{
if左右子树都为空,return true;
if左右子树只有一个为空,return false;
左右子树的值相等,一直递归调用
return (p->val==q->val) && isMirror(p->left,q->right) && isMirror(p->right,q->left);
}
2.2.3 运行结果
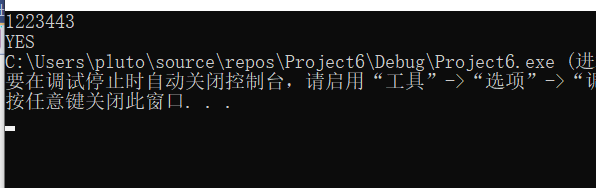
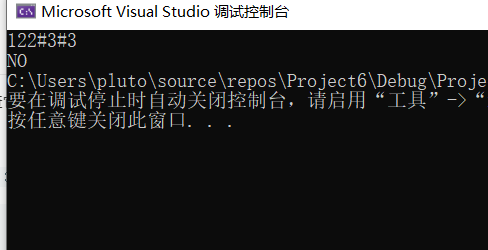
2.2.4分析该题目解题优势及难点。
解题优势:return (p->val==q->val) && isMirror(p->left,q->right) && isMirror(p->right,q->left)感觉很厉害,即判断了值相等不
还厉害了镜像对称的特点,左子树的左子树跟右子树的右子树对应,左子树的右子树跟右子树的左子树对应
难点:递归函数的设计和镜像对称用代码的表示
2.3 题目及解题代码
题目:路径总和


2.3.1 该题的设计思路
1、判断边界条件。(1)root为null。(2)root左右子树为null。
2、深度搜索左右子树。
2.3.2 该题的伪代码
bool hasPathSum(TreeNode* root, int sum)
{
return DFS(root, sum);//判断是否存在所给路径和
}
bool DFS(TreeNode* root, int sum)
{
if(root==NULL)说明前面都不满足路径和的值,return NULL;
if(左右子树都为空)
if(root的值为sum)return true;
递归调用,sum的值每次减小root->val;
return (DFS(root->left, sum-root->val) || DFS(root->right, sum -root->val);
}
2.3.3 运行结果

2.3.4分析该题目解题优势及难点。
解题优势:代码易懂,巧妙设计递归参数的值,每次递归都使sum的值减少,逆向求路径和
难点:函数参数的值的设计,题目的理解也有一定难度
2.4 题目及解题代码
题目:二叉树的最小深度


2.4.1 该题的设计思路
思路:遇到叶子节点不递归而是返回值,遇到其他节点则继续递归
2.4.2 该题的伪代码
int minDepth(TreeNode* root)
{
if(root为空) return NULL;
int level=1;
if(root为叶节点) return level;
若左孩子空,求右子树深度;
return level+minDepth(root->right);
若右孩子空,求左子树深度;
return level+minDepth(root->left);
最后求都不空的情况
return level+min(minDepth(root->left),minDepth(root->right));
}
2.4.3 运行结果

2.4.4分析该题目解题优势及难点。
解题优势:函数设计巧妙,且代码简洁,用min来取左右的最小深度
题目难度:读清题意,是叶子的最小深度,函数的返回值的设计

 浙公网安备 33010602011771号
浙公网安备 33010602011771号