DS博客作业02--栈和队列
2020-03-22 16:29 pluto1214 阅读(334) 评论(0) 收藏 举报0.PTA得分截图

1.本周学习总结
1.1 总结栈和队列内容
栈的知识总结
顺序栈的知识 链栈的知识
存储结构 结构存储
typedef struct stack //定义一个顺序栈 typedef struct LinkStack
{ {
ElemType data[M];//栈中最多可放M个元素 ElemType data;
int top;//用来存放栈顶元素的下标,top为-1表示栈空 struct LinkStack*next;
} Stack,*SeqStack; }LiNode, * LiStack;
栈的初始化 链栈的初始化
void InitStack(SeqStack s)//初始化一个栈 void InitStack(SeqStack& s)//初始化一个链栈
{ {
s=new Stack;
s->top=-1;//此时栈空,且其为判断栈是否为空的条件 s=new LiNode;
} s->next=NULL;
}
进栈操作 进栈操作
bush push(SeqStack s,ElemType x) void push(LiStack& s, char a)
{ {
if(s->top==MaxSize-1)//顺序栈需判断栈是否满了 LiStack p=new LiNode;
return false; p->data=a;
s->top++; p->next=s->next;
s->data[s->top]=x; s->next=p;
return true;
} }
出栈操作 出栈操作
bush pop(SeqStack s,int *x) bool pop(LiStack& s)
{ {
if(s->top==-1)//栈空则无法进行出栈 if(s->next=NULL)
return false; return false;
*x=s->data[s->top]; LiStack q;
s->top--; q=s->next;
return true; s->next=q->next;delete q;
} return true;
}
取栈顶元素 判断链栈是否为空
bool GetTop(SeqStack s,char *a) //取栈顶元素 bool Empty(LiStack& s)
{ {
if(s->top==-1)//栈空则不能取栈顶 if(s->next==NULL)
return false; return true;
else else
{ return false;
*a=s->data[s->top]; }
return true;
}
}
判断栈是否为空
bool IsEmpty(SeqStack s) //判断栈空
{
if(s->top==-1)
return true;//空的时候才返回true,与习惯不同
else
return false;
}
栈的应用:
1.浏览器的浏览记录是后浏览的出现在前面,可见是利用了栈后进先出的特点
2.栈还可以运用于保存走出迷宫的路径,但路径是逆序的
3.栈应用于括号的匹配,将括号的左边进栈,碰到右括号再取栈顶匹配
4.中缀表达式转后缀表达式也是用栈,利用不断进栈出栈实现表达式的转换
栈的相关图解
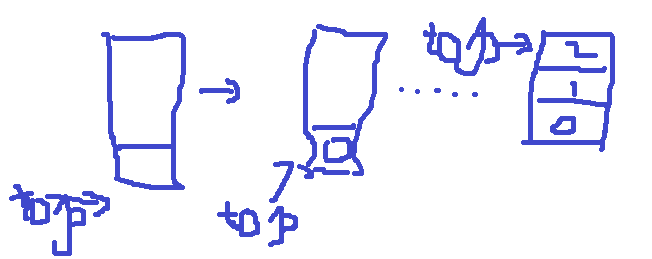
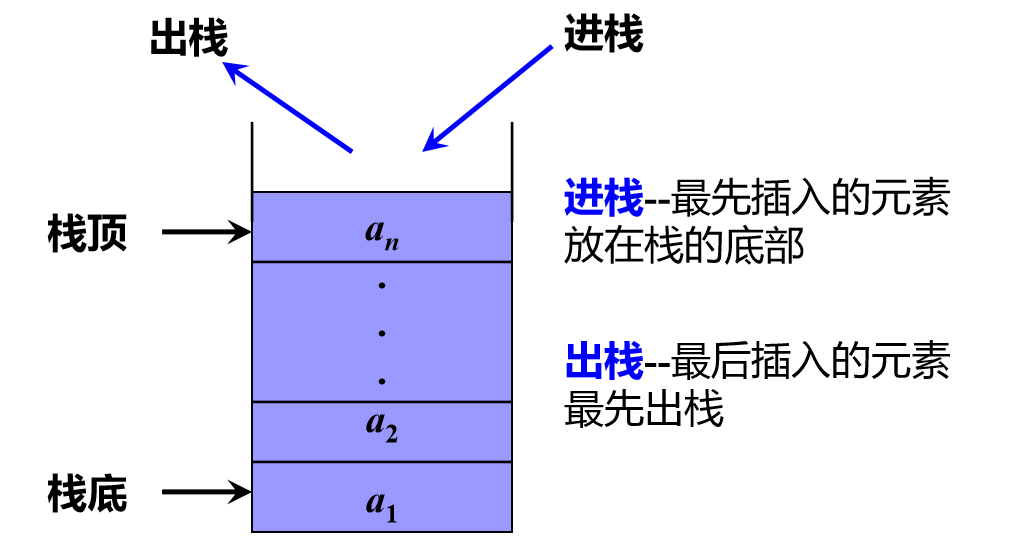
队列的知识总结
队列的相关概念:
队头与队尾:允许元素插入的一端称为队尾,允许元素删除的一端称为队头。
入队:队列的插入操作。
出队:队列的删除操作。
队列的存储结构: 循环队列的存储结构
typedef struct SqQueue typedef struct SqQueue
{ {
int data[maxsize]; int*data;
int front;//队首指针 int front;
int rear;//队尾指针 int rear;
}SqQueue,*Queue; int maxsize;
}SeQueue,*Queue;
初始化队列 初始化循环队列
void InitQueue(Queue &Q) void InitQueue(Queue &Q,int n)
{ {
Q->data=new int[maxsize];
Q->front=-1; Q-front=Q->rear=0;
Q->rear=-1; Q->maxsize=n;
} }
判断队列是否空 循环队列插入
bool EmptyQueue(Queue &Q) void EnQueue(Queue& Q,int e)
{ {
if(Q->front==Q->rear) if((Q->rear+1)%Q->maxsize==Q->front)//循环队列满
{ return false;
return true;//队列空 Q->rear=(Q->rear+1)%Q->maxsize;
} Q->data[Q->rear]=e;
else }
{
return false;
}
}
入队列 循环队列删除操作
bool EnQueue(Queue &Q,int e) void DeQueue(Queue& Q)
{ {
if(队满) if(Q->front==Q->rear)
return false; return ;
Q->rear++; Q->front=(Q->front+1)%maxsize;
Q->data[Q->rear]=e; }
return true;
}
出队列
bool DeQueue(Queue &Q)
{
if(对空)
return false;
Q->front++;
return true;
}
队列的应用:
1.队列可应用于找迷宫的出口,并且由于是广域搜索,所找路径是最短路径
2.应用与报数游戏,数到n的出队,其余的出队再入队,便可实现排序
3.现实生活中排队类的问题,与队列先进先出的特点相同
链队列和链栈的操作利用STL容器直接实现
stack<类型名> s//创建并初始化栈; s.pop()//出栈但不返回出栈元素
s.push(e)//入栈 s.top()//访问栈顶 s.empty()//判断栈空
s.size()//访问栈中元素个数
queue<类型名> s//创建并初始化栈;
s.push(e)将e插入队列末端 s.front()访问队列第一个元素
s.pop()删除队列的第一个元素 s.back()访问队列末尾的元素
s.empty()判断队列是否为空 s.size()访问队列中元素个数
队列的图形结构

1.2.谈谈你对栈和队列的认识及学习体会。
栈和队列的应用很灵活,其都具有各自的特点,在解决一些问题的时候可以根据栈先进后出而
队列先进先出的特点更快地解题,同时栈和队列也更贴近实际生活的一些应用了,例如浏览器
的浏览记录,迷宫等,感觉涉及到一些实际应用比较有趣。
2.PTA实验作业
2.1.题目1:7-5 表达式转换 (25分)
2.1.1代码截图

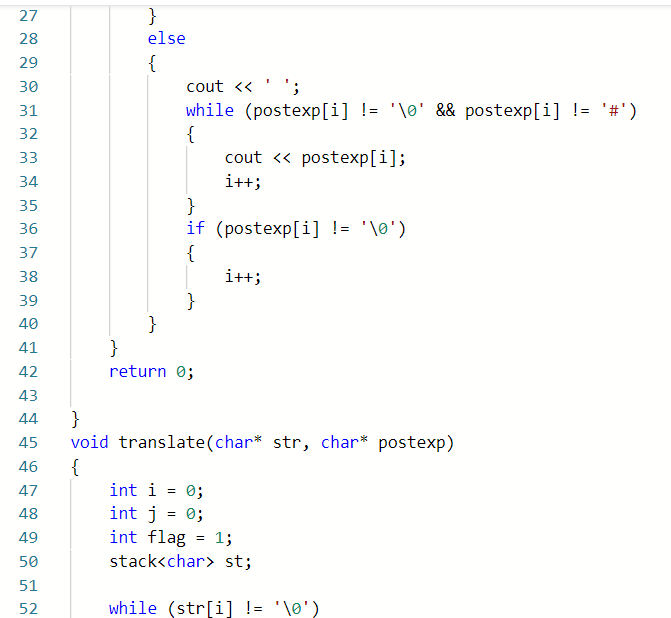
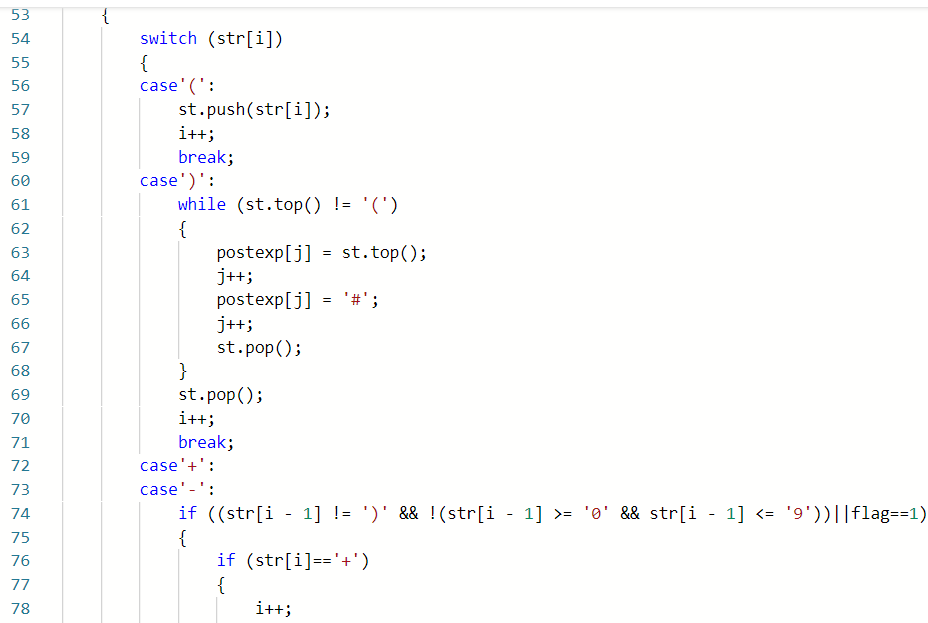



2.1.2本题PTA提交列表说明。

Q1:只拿了一分,就最后一个只输入一个数字的测试点对,而头三个一开始是答案错误,后来是格式错误并且不能正确表示两位及以上数字
A1:代码中有很多问题,遇到右括号出栈后,再将最后左括号也出栈解决一个问题,小数点同数字一起存入postexp后缀表达式中又解决一个问题,
还有就是扫描str后再将栈中剩余的元素存入后缀表达式中,但是我在输出时是有数字就空格,导致本来输出21结果输出了2 1,于使我将一个数字
后加上#以区别,使得十位数字和百位数字等都能正确输出
Q2:运算数前有正负号过不去,修改了很多次代码还是错误
A2:一开始我先分为第一个元素和不是第一个元素处理,但那样子非常麻烦,越错思路越乱。后面思考后发现只要第一个数是’+’或’-‘时判断是运
算符还是正负号就行了。修改后代码简洁很多,答案也正确。但问题还有,还是过不去那个测试点,后面造了很多数据测试,问题在于正号不用输
出,即1+(+5),输出时5前面没有+号。加入以下代码此题目完成
if (str[i]=='+')//此处+表示正号
{
i++;
continue;
}
2.2.题目2:7-3 jmu-ds-符号配对 (15分)
2.2.1代码截图



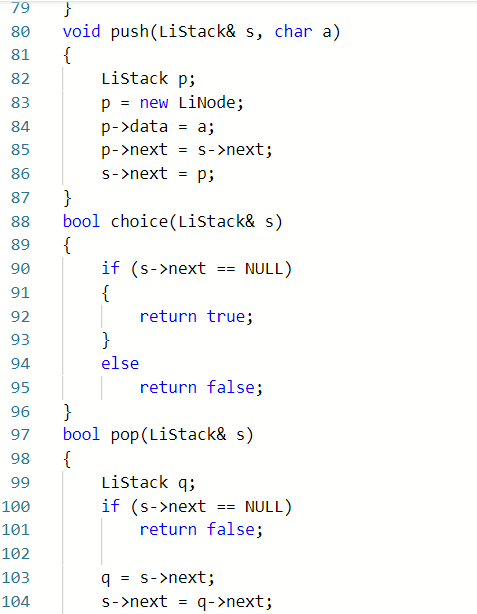

2.2.2本题PTA提交列表说明。
*Q1:扫描之后没有考虑栈空不空的情况,当(()时则还要输出(
A1:扫描后根据栈空还是不空分别进行输出
Q2:提交列表总是有错误,我以为是我扫描过后对于flag和栈空不空的判断条件有错误,但实际上是因为我在扫描到)
而栈空时没有立即结束,而是break,下面的括号不配对也是,在测试多种数据后发现会重复输出,比如输入(1}时,
本应输出}和no,但由于我用break,导致我会输出这个结果两次。
A2:将break改为return 0;*
3.阅读代码
3.1 题目及解题代码
题目:判断一个字符串是否可由另一个字符串出栈得到
代码:
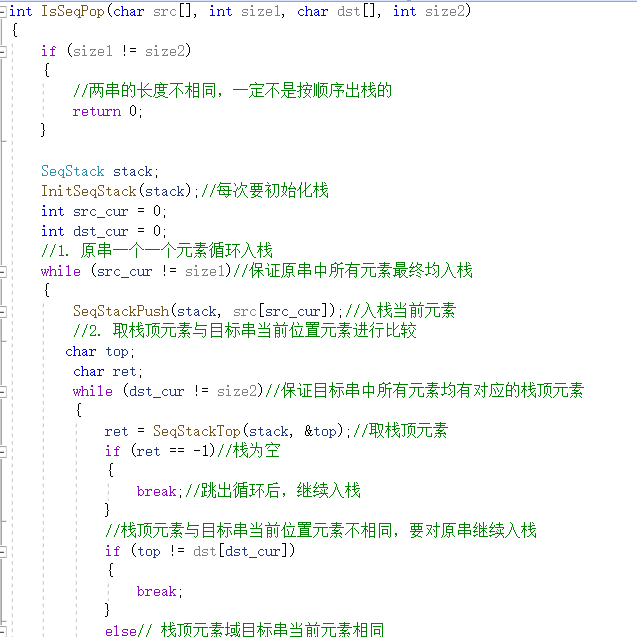

3.1.1 该题的设计思路

3.1.2 该题的伪代码
while(src_cur!=size1)//s1没全部入栈,src_cur为s1中当前的位置
{
SeqStackPush();//入栈当前元素
while(dst_cur!=size2)//s2没全部入栈,dst_cur为s2中当前的位置
{
取栈顶元素top,取失败栈空则break;
if(top!=dst[dst_cur) break;
出栈一个元素;
dst_cur++;//目标串当前位置后移,继续比较栈顶元素域目标串当前位置元素
}
src_cur++;
}
3.1.3 运行结果

3.1.4分析该题目解题优势及难点。
解题优势:思路清晰,代码易懂,灵活的利用了取栈出栈来解题,用src_cur和dst_cur来取字符串中的元素
难点:本题的难点主要在于如何解题,我看到题目时一点都不清楚如何下手,想到栈可进又可随时出栈顶更觉得题目复杂
3.2 题目及解题代码
题目:出栈序列的合法性
给定一个最大容量为 M 的堆栈,将 N 个数字按 1, 2, 3, ..., N 的顺序入栈,允许按任何顺序出栈,则哪些数字序列是
不可能得到的?例如给定 M=5、N=7,则我们有可能得到{ 1, 2, 3, 4, 5, 6, 7 },但不可能得到{ 3, 2, 1, 7, 5, 6, 4 }。
代码:


3.2.1 该题的设计思路

3.2.2 该题的伪代码
for (int i = 0; i < K; i++)
{
int c = 1;
int j = 0;
while(j<N)
{
while(栈不空且栈顶元素不等于a[i][j])
{
if(c>N)flag=1;break;//进栈的数不能大于待测序列最大数
否则进栈;
c++;
}
if(flag==1||栈的个数大于M)
输出no,break;
否则
while(栈不空且栈顶与a[i][j]相等&&j<N时)
删除栈顶元素;j++;//j++是移动到待测序列下一个数
}
}
3.2.3 运行结果

3.2.4分析该题目解题优势及难点。
解题优势:很好的利用栈先进后出的特点,按1,2,3从小到大进栈,相等时出栈直到不相等,
若能在flag=1之前使栈为空,便能说明该序列的顺序是合法的
难点:题目不容易懂,代码难以设计,需考虑很多情况,思路也比较难理解

 浙公网安备 33010602011771号
浙公网安备 33010602011771号